
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий метод составления уравнений нелинейных САУСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сначала выполняется, где возможно, линеаризация звеньев. При этом используются различные методы, например, разложение нелинейной функции в ряд Тейлора в окрестностях некоторой точки. В результате остаются неописанными так называемые существенно нелинейные звенья. Обычно их не более одного-двух. Затем составляют уравнения для этих звеньев со всеми возможными упрощениями их характеристик. Получается система обыкновенных линейных уравнений, к которым добавляется одно-два нелинейных уравнения. В соответствии с этим, обобщенную структурную схему любой НСАУ при наличии одного нелинейного звена можно представить в виде (рис. 73).
Рис. 73. Обобщенная схема НСАУ с одним нелинейным звеном Имеется одно нелинейное звено (НЗ) и линейная часть САУ (ЛЧ САУ). Все НСАУ делятся на два больших класса. 1. Уравнение нелинейного звена имеет любой вид, но под знаком нелинейной функции либо только входная (или ее производные) величина, либо только выходная (или ее производные) величина. Такую систему можно свести к нарисованной выше схеме. 2. Любое число нелинейных звеньев. Под знак нелинейной функции входят обычные переменные, но связанные друг с другом линейной передаточной функцией. Процессы в НСАУ имеют существенные особенности, поэтому их анализ является сложным. Это касается и устойчивости. С точки зрения устойчивости система имеет несколько состояний. 1. Устойчивое равновесное состояние с постоянным значением регулируемой величины. 2. Устойчивые автоколебания (собственные колебания с постоянной амплитудой) при отсутствии внешнего воздействия. 3. Область неустойчивости. 4. Области, соответствующие другим, более сложным случаям. В таких системах можно говорить об устойчивости в «малом» и в «большом». Система устойчива в «малом», если существуют начальные условия, которые не выводят выходные отклонения за определенную величину. Если же существуют начальные условия, которые выводят выходные отклонения за определенную величину, то система неустойчива в «большом» (рис. 74).
Рис. 74. Устойчивость НСАУ Фазовое пространство Для наглядного представления процессов нелинейных САУ вводится понятие «фазовое пространство», которое заключается в следующем. Дифференциальное уравнение замкнутой системы n -го порядка заменяется системой дифференциальных уравнений первого порядка.
где x 1 – выходная величина; x 2 – xn – вспомогательные переменные; f, g – входные воздействия (возмущающее и задающее); x 10 = x 1(t = 0), x 20 = x 2(t = 0) … – начальные условия. Эти дифференциальные уравнения можно представить геометрически в n -мерном пространстве. Например, при n = 3 (рис. 75).
Рис. 75. Трехмерное фазовое пространство В реальном процессе управления в каждый момент времени величины x 1, x 2, x 3 имеют вполне определенные значения. Это соответствует вполне определенному положению точки М в пространстве. Точка М называется изображающей. С течением времени величины x 1, x 2, x 3 изменяются, точка М перемещается по определенной траектории, показывая так называемую фазовую траекторию. Следовательно, траектория движения точки М может служить наглядной геометрической иллюстрацией динамического поведения САУ в процессе управления. Рассмотрим пример фазовых траекторий некоторых линейных САУ. Пусть они описываются уравнением Рис. 76,а соответствует комплексным корням с отрицательной вещественной частью (наличие затухающего переходного процесса), случай рис. 76,б показывает фазовую траекторию апериодического затухающего процесса при отрицательных вещественных корнях характеристического уравнения. ДУ представляют собой выражения для проекций скорости изображающей точки М на óси координат. Поэтому по значениям правых частей уравнений в каждый момент времени можно судить о движении точки М, и, следовательно, о поведении реальной НСАУ в процессе управления. Фазовая траектория – это качественная характеристика НСАУ. Для определения количественных значений выходных сигналов необходимо решать дифференциальные уравнения в каждой точке. Если дифференциальные уравнения составлены для отклонений выходного сигнала от установившихся значений, то для устойчивой системы фазовая кривая будет стремиться в начало координат.
б) Рис. 76. Примеры фазовых траекторий Устойчивость по Ляпунову Для нелинейных систем существует понятие устойчивости по Ляпунову. Невозмущенное движение (установившийся процесс) называется устойчивым, если при заданной сколь угодно малой области e можно найти такую область h, что при начальных условиях, расположенных внутри этой области, переходный процесс будет таким, что изображающая точка не выйдет из области e при любом сколь угодно большом значении времени t (рис. 77). Аналитически условие можно представить в следующем виде. При начальных условиях
Рис. 77. Устойчивость по Ляпунову Гармоническая линеаризация Данный метод используется для приближенного определения наличия автоколебаний и устойчивости нелинейных систем любого порядка. Пусть дано некоторое нелинейное выражение вида Разложим функцию F в ряд Фурье:
Предположим, что первое слагаемое равно нулю, т. е. в разложении нет постоянной составляющей. Если принять во внимание, что из исходных выражений следует
где q и q ¢ – коэффициенты гармонической линеаризации.
Таким образом, исходное уравнение при х = а sinw t с точностью до высших гармоник аналогично линейному. В этом и заключается метод гармонической линеаризации. Если значения амплитуды a и частоты w постоянны (периодический процесс), то и коэффициенты q и q ¢ постоянны. В переходном процессе амплитуда и частота непостоянны. В этом и заключается отличие данного метода от обычных методов линеаризации. Это отличие позволяет при анализе систем обнаружить особенности работы НСАУ. Рассмотрим простой частный случай y = F (x). Если эта кривая не имеет гистерезисной петли, то q ¢ = 0. Тогда Таким образом, криволинейная характеристика заменяется прямой линией, тангенс угла которой зависит от амплитуды входного сигнала. Найдем гармонически линеаризованное уравнение для замкнутой нелинейной системы в целом. Линейная часть описывается ДУ следующего вида любой сложности:
Нелинейная часть описана простым соотношением:
После линеаризации уравнение нелинейного звена будет иметь вид:
Уравнение не имеет высших гармоник. Объясняется это следующим. Как правило, в замкнутой САУ линейная часть обладает свойствами низкочастотного фильтра. Это легко обнаружить при рассмотрении ЛАЧХ линейной замкнутой САУ. Общее характеристическое уравнение замкнутой НСАУ имеет вид:
Если в системе имеют место автоколебания, т. е. имеются незатухающие колебания с амплитудой а П и частотой wП, то коэффициенты этого уравнения становятся постоянными. С другой стороны, из теории линейных САУ следует, что имеет место пара чисто мнимых корней характеристического уравнения. Поэтому, чтобы определить автоколебания нелинейных САУ, можно найти границу устойчивости соответствующей линейной САУ, т. е. можно воспользоваться критериями устойчивости линейной САУ (алгебраическими и частотными). Заключение В пособии были рассмотрены вопросы проектирования систем автоматического управления. Особое внимание было уделено вопросам анализа и синтеза непрерывных линейных САУ. Кратко представлен раздел нелинейных систем. Представленный материал дает теоретическую базу для исследования дискретных и цифровых систем управления, изучение которых выходит за рамки данного курса. ЛИТЕРАТУРА 1.Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. – М.: изд. Наука, гл. ред. физ-мат. лит. – 1975, 768 с. 2.Сборник задач по теории автоматического регулирования и управления, под ред. В. А. Бесекерского. – М.: гл. ред. физ-мат. лит. – 1972, 588 с. 3. Попов Е. П. Теория линейных систем автоматического регулирования и управления. Учебное пособие – М.: Наука, 1989. 4. Солодовников В. В., Плотников В. Н., Яковлев А. В. Основы теории и элементы систем автоматического регулирования. Учебное пособие. – М.: Машиностроение, 1985. 5. Теория автоматического управления /Под ред. А. А.Воронова – М.: Высшая школа, 1987.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.176 (0.01 с.) |



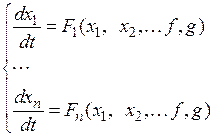 ,
,
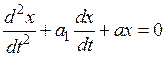 . В зависимости от параметров ДУ возможно несколько случаев. Некоторые из них представлены на рис. 76.
. В зависимости от параметров ДУ возможно несколько случаев. Некоторые из них представлены на рис. 76.
 а)
а) решение ДУ переходного процесса удовлетворяет неравенствам
решение ДУ переходного процесса удовлетворяет неравенствам  при любом сколь угодно большом t, начиная с некоторого t = T > 0.
при любом сколь угодно большом t, начиная с некоторого t = T > 0.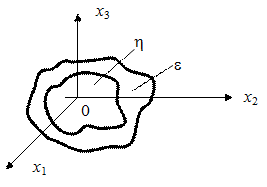
 и задано
и задано  ;
;  . Тогда
. Тогда  .
.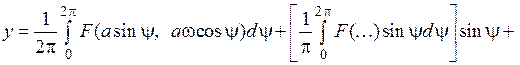
 высшие гармоники.
высшие гармоники. и
и  , то можно получить
, то можно получить + высшие гармоники,
+ высшие гармоники, ;
; .
. + высшие гармоники;
+ высшие гармоники; .
. .
. .
. .
.


