
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет установившейся ошибки САУСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Замкнутая система может находиться под воздействием случайного задающего сигнала g (t), и случайной помехи f (t), приложенной в произвольной точке системы (рис. 72). Корреляционные функции и спектральные плотности и полезного сигнала и помехи известны. Конечная цель – нахождение корреляционной функции и спектральной плотности ошибки x (t) и выходного сигнала y (t).
Рис. 72. Случайный задающий сигнал и случайная помеха в САУ Обычно ограничиваются более узкой задачей: нахождением среднеквадратичной ошибки (СКО) системы управления. Возможны следующие случаи. 1. Имеется входной сигнал g (t) – случайный стационарный процесс. Помеха f (t) = 0. Тогда спектральная плотность ошибки
где СКО будет равно
2. Имеется помеха f (t), задающее воздействие g (t) = 0. Справедливы соотношения
Если же помеха действует на входе системы, то расчет СКО аналогичен первому случаю. 3. Имеется и сигнал и помеха. Общее выражение для спектральной плотности ошибки
где Sfg (w)и Sgf (w) – взаимные спектральные плотности сигнала и помехи; знак «*» показывает сопряженную комплексную величину. Если корреляции между сигналом и помехой нет, третье и четвертое слагаемые в выражении равны нулю. Аналогичным образом можно найти и параметры для выходного сигнала y (t). При этом необходимо использовать частотную передаточную функцию замкнутой системы
Расчеты по минимуму ошибки Если на систему одновременно действует полезный сигнал и помеха, то может быть решена задача оптимального расчета системы с тем, чтобы обеспечить наименьшую результирующую ошибку системы. Критерием является минимальное значение результирующей ошибки системы, определяемой сигналом и помехой. Для случайных процессов обычно ограничиваются оценкой среднеквадратической ошибки. Необходимо обеспечить минимум среднеквадратической ошибки при одновременном действии сигнала и помехи. Критерий выглядит следующим образом:
Нежелательность ошибки пропорциональна квадрату ее величины. Возможны две формулировки данной задачи. 1. Имеется САУ заданной структуры. Необходимо так выбрать ее параметры, чтобы обеспечить минимум СКО при заданных статистических параметрах сигнала и ошибки.
Решение ищется следующим образом: зная спектральную плотность ошибки, теоретически находится выражение для расчета дисперсии и СКО. Это выражение зависит от параметров системы, полезного сигнала и помехи. Ищутся условия на параметры системы для обеспечения минимума дисперсии. В простых случаях можно применить известные методы нахождения экстремума функции путем дифференцирования и приравнивания к нулю частных производных. 2. Ставится вопрос о нахождении оптимальной структуры системы и параметров звеньев для получения теоретически минимальной среднеквадратической ошибки при заданных вероятностных характеристиках полезного сигнала и помехи. Решение следующее: находится теоретическая передаточная функция замкнутой системы, и к ней стремятся при проектировании. Возможна ситуация, что реализация САУ с такой оптимальной передаточной функцией будет сопряжена со значительными трудностями. Нелинейные САУ Анализ нелинейных САУ (НСАУ) представляет собой достаточно трудную задачу. При ее решении стремятся свести такую САУ к линейной с определенными допущения и ограничениями. К таким системам относятся те, в которых имеется хотя бы одно звено, описываемое нелинейными дифференциальными уравнениями. Нелинейные звенья могут быть следующих видов: - релейного типа; - с кусочно-линейной характеристикой; - с криволинейной характеристикой любого очертания; - имеется произведение и другие комбинации переменных; - нелинейное звено с запаздыванием; - импульсное звено; - логическое; - описываемое кусочно-линейным дифференциальным уравнением. Нелинейности могут быть статические и динамические. Статические описываются нелинейными статическими характеристиками, а динамические – нелинейными дифференциальными уравнениями.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.123.103 (0.01 с.) |

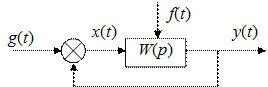
 ,
,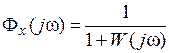 – передаточная функция замкнутой системы по ошибке.
– передаточная функция замкнутой системы по ошибке. .
. ;
; .
.
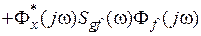 ,
, .
. .
.


