
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 3. Нелинейные системы автоматичекого управленияСодержание книги
Поиск на нашем сайте МОДУЛЬ 3. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕКОГО УПРАВЛЕНИЯ
РАЗДЕЛ 5. НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕЛИНЕЙНЫХ САУ Особенности нелинейных систем управления Рассмотренные ранее системы, в том числе и импульсные, описываются линейными дифференциальными уравнениями. Однако существуют системы, которые могут быть описаны только нелинейными дифференциальными уравнениями. Если система содержит хотя бы одно нелинейное звено (НЗ), то она называется нелинейной САУ. Нелинейные системы часто встречаются на практике. Вообще большинство САУ является нелинейными и лишь для упрощения задач анализа и синтеза проводится их линеаризация, то есть НЗ заменяется приближенным линейным при ограниченных пределах изменения входной величины. Существуют нелинейные объекты регулирования. Кроме того, НЗ вводят в систему преднамеренно для улучшения качества процесса регулирования. Перед теорией регулирования нелинейных систем стоят задачи: 1) Анализ, то есть исследование процессов в НЗ, исследование устойчивости и качества переходных процессов нелинейных систем. 2) Синтез, то есть выбор корректирующих устройств, параметров или структуры с целью получения заданного качества переходных процессов. ТАУ нелинейных систем имеет особенности: 1. При анализе процессов в нелинейных системах нельзя использовать принцип суперпозиции, так как в нелинейных системах качественные показатели переходной характеристики зависят от уровня входного сигнала.
Для нелинейных систем нельзя использовать принцип суперпозиции, так как реакция на ступенчатый сигнал может иметь вид (рис. 26.2).
Это затрудняет исследование нелинейных систем. И для нелинейных систем теряют смысл показатели качества систем при единичном входном воздействии, такие как tp и s%. 2. В нелинейных САУ иначе рассматривается вопрос устойчивости. Если в линейных САУ незатухающие колебания являются признаком неработоспособности системы, то в нелинейных системах такой режим является допустимым, а иногда и единственно возможным и под устойчивостью в этом случае понимается устойчивость автоколебаний. При исследовании нелинейных систем часто используют понятие устойчивости в некоторой области. В этом случае понятие устойчивости для нелинейных систем совпадает с понятием устойчивости для линейных систем. 3.Нелинейные системы описываются нелинейными дифференциальными уравнениями и сложность решения нелинейных дифференциальных уравнений привела к созданию ряда приближенных методов. Существует аналитические и графические методы, а также широко применяют ЭВМ. Для решения задач анализа и синтеза систем разработаны методы. Точные: метод припасования, метод фазовой плоскости. Приближенные: метод гармонической линеаризации, метод гармонического баланса и метод статистической линеаризации. Теория нелинейных систем разработана в трудах российских ученых: Крылова А. Н, Боголюбова Е. В., Андронова А. А, Попова Е. П. и других. Общие характеристики НЗ Характеристика нелинейного одномерного звена может быть записана следующим образом
Свойства нелинейной функции. 1) Симметрия
 удовлетворяет условию удовлетворяет условию  , то она симметрична относительно оси ординат. , то она симметрична относительно оси ординат.
б) Если функция
2) Гладкость. Если в любой точке 3) Однозначность. Если каждому значению x1 соответствует одно значение x2, то характеристика называется однозначной, если несколько значений, то неоднозначной.
Характеристиками
2) Звено типа “зона нечувствительности”.
3) Звено типа “ограничение + зона нечувствительности”.
На выходе системы
Пусть в обоих случаях входные сигналы “ x ” равны, тогда из (26.1) и (26.2) следует, что выходные сигналы не равны. Следовательно, при последовательном соединении нелинейных звеньев не выполняется принцип коммутативности, поэтому НЗ нельзя менять местами.
2) Параллельное соединение
x = x1 = x2
3) Встречно– параллельное соединение звеньев.
Выходная величина выражена в этом случае неявно. Критерий Сильвестра. Квадратичная форма (28.12) положительно определенная, если все “ n ” определителей |P1|,|P2|,…,|Pn| – положительны. Пример:
Определение устойчивости линейной системы. Дифференцирование функции Ляпунова в виде (28.12). Пусть имеем линейную автономную систему, которая описывается уравнением состояния
Тогда сопряженная система будет иметь вид
Пусть V( Тогда найдем производную функции Ляпунова по времени с учетом (28.13) и (28.14)
Введем обозначение
Тогда если матрица Q положительно определена, то система (28.13) асимптотически устойчива, так как
Эти результаты применяют при синтезе адаптивных систем управления, которые обычно содержат в своем составе как линейные, так и нелинейные части.
29.УСЛОВИЯ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
МОДУЛЬ 3. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕКОГО УПРАВЛЕНИЯ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 ,где
,где  – нелинейная функция, которая может иметь определенные свойства. Нелинейное звено можно представить в структурной форме (рис. 26.3)
– нелинейная функция, которая может иметь определенные свойства. Нелинейное звено можно представить в структурной форме (рис. 26.3) F(x1)
F(x1)
 , то нелинейная функция обладает симметрией относительно начала координат.
, то нелинейная функция обладает симметрией относительно начала координат. , то нелинейная характеристика называется гладкой.
, то нелинейная характеристика называется гладкой. (26.2)
(26.2)




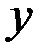





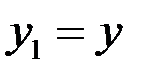



 так как р12 = р21.
так как р12 = р21. (28.13)
(28.13) (28.14)
(28.14) )=xTPx – функция Ляпунова.
)=xTPx – функция Ляпунова.
 (28.16)
(28.16)



