
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод гармонической линеаризации нелинейностейСодержание книги
Поиск на нашем сайте
Из-за трудностей описания нелинейные системы обычно сводят, если это возможно, к линейным. Ранее была рассмотрена линеаризация вблизи рабочей точки, однако она требует непрерывных нелинейных функций и малых отклонений переменных, это – линеаризация во временной области. Гармоническая линеаризация – это линеаризация в частотной области. При этом нелинейный элемент заменяется линейным, но эквивалентным исходному, только относительно основной составляющей колебаний. Гармоническая линеаризация может успешно применяться в случае разрывных кривых и значительных отклонений переменных. Этот метод нашел широкое применение для определения автоколебательных процессов и устойчивости нелинейных систем. Является мощным методом исследования, так как применяется для систем любого порядка. Единственное ограничение: необходимо, чтобы линейная часть системы обладала хорошими фильтрующими свойствами, то есть подавляла все гармоники, кроме первой. Пусть имеем НЗ, которое описывается уравнением:
где x1 – сигнал на входе НЗ; x2 – сигнал на выходе НЗ; p – оператор дифференцирования. Пусть сигнал на входе НЗ
Тогда
Выходной сигнал НЗ, соответствующий уравнению (27.1), может быть разложен в ряд Фурье
где
Пусть a0 = 0, то есть постоянная составляющая равна нулю. Из (27.2) и (27.3) имеем
Тогда (27.4) можно записать следующим образом:
где Таким образом, при Эта операция называется гармонической линеаризацией. Если на входе НЗ действует сигнал с постоянной амплитудой и частотой, то Рассмотрим гармоническую линеаризацию для простой нелинейной зависимости
Здесь возможны два случая. 1. Нелинейная характеристика имеет петлю гистерезиса (рис. 27.1).
В этом случае выходной сигнал будет зависеть от знака производной входного сигнала.
Тогда, если на вход действует сигнал
то Высшими гармониками ряда в выходном сигнале пренебрегают. Коэффициенты гармонической линеаризации
2. Нелинейная характеристика не имеет гистерезисной петли (рис. 27.2). В этом случае при x = x1 = a sinψ, dx = a cosψ dψ.
Новые пределы интегрирования для переменой x: ψ = 0 => x = 0, ψ= 2π => x = 0,
Таким образом, получим
Следовательно, при отсутствии гистерезисной петли уравнение после линеаризации имеет вид
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.253.217 (0.009 с.) |

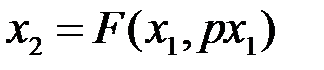 (27.1)
(27.1)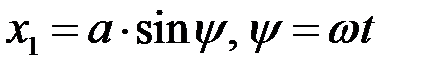 . (27.2)
. (27.2)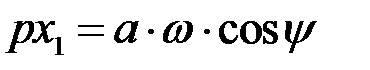 . (27.3)
. (27.3) (27.4)
(27.4)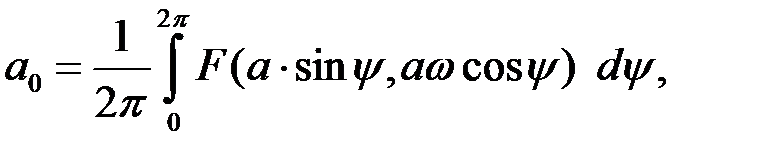
 (27.5)
(27.5)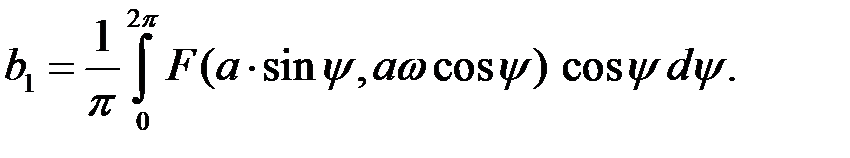
 (27.6)
(27.6)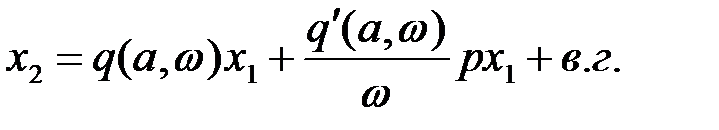 . (27.7)
. (27.7)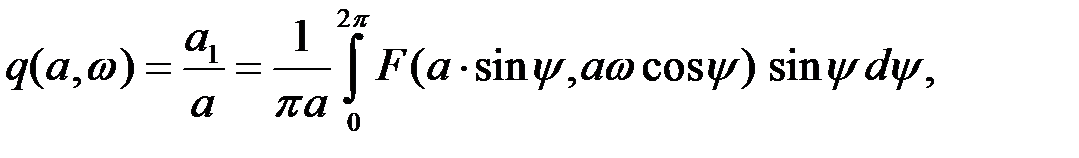
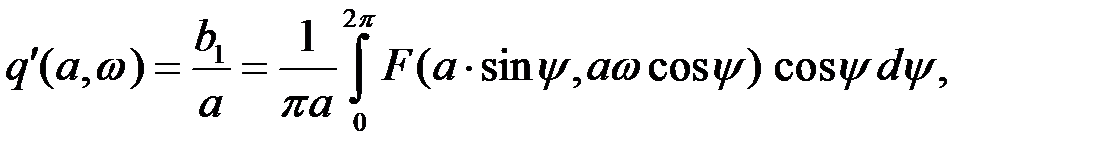
 и
и 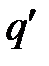 – коэффициенты гармонической линеаризации.
– коэффициенты гармонической линеаризации. (27.1) заменяем уравнением (27.7), которое с точностью до высших гармоник аналогично линейному.
(27.1) заменяем уравнением (27.7), которое с точностью до высших гармоник аналогично линейному. .
. . (27.9)
. (27.9)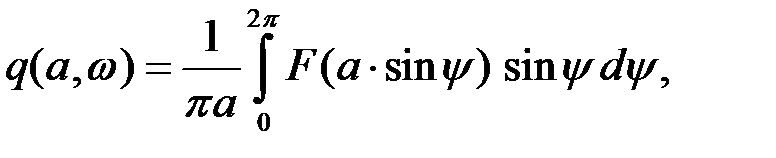
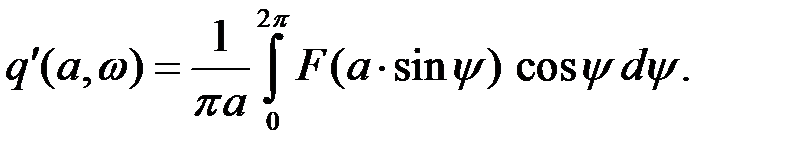


 .
.


