
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автоколебательного режима и его устойчивостиСодержание книги Поиск на нашем сайте
Практически пользоваться выражением (27.17) неудобно, так как требуется подобрать два параметра Для этого запишем (27.17) следующим образом
где:
Уравнение (27.18) можно решить графически. Для этого нужно построить на комплексной плоскости годографы линейной части системы
и обратного комплексного коэффициента передачи НЗ
Параметры их определяются следующим образом: значение частоты Пересечение графиков показывает, что в системе возможны автоколебания. Следующим этапом является определение устойчивости этих автоколебаний.
52 Анализ устойчивости системы и устойчивости предельного цикла
Запишем условие гармонического баланса в следующем виде.
Здесь
Уравнение (27.20) можно представить в виде двух уравнений
Допустим, получили следующее расположение годографов (рис. 27.14).
Пусть весь годограф нелинейного звена лежит в области D 0, то есть условие (27.20) не выполняется, так как Аналогично можно показать, что если весь годограф Если годографы пересекаются (рис. 27.15), то в системе возможны автоколебания в точках 1 и 2. Определим, где автоколебания устойчивы? В точке 1– амплитуда – а п; в точке Пусть существуют автоколебания в точке 1 с параметрами а п и ωп. Допустим, произошло увеличение амплитуды а п + ∆a (точка
Пусть амплитуда колебаний уменьшается, то есть а п – ∆a (точка Следовательно, точка 1 соответствует устойчивому предельному циклу. Рассмотрим точку 2. Пусть а понижается, то есть а п – ∆a (точка 2′). В этом случае система устойчива и колебания затухающие. Следовательно, точка 2 соответствует неустойчивому предельному циклу. На основе проведенного анализа сформулируем правило определения устойчивости автоколебаний: автоколебания устойчивы, если годограф Пример. Метод гармонического баланса. Дана нелинейная система следующего вида (рис. 27.16). Параметры системы равны: Определить, возможны ли автоколебания и если возможны, то найти их параметры.
Для решения воспользуемся условием гармонического баланса
в соответствии, с которым следует построить годографы Построим годограф
где
Тогда обратный комплексный коэффициент передачи примет вид
Построим его.
Годограф линейной части строим по выражению
Автоколебания возможны и имеют параметры:
53 МЕТОД ЛЯПУНОВА 28.1. Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях Пусть имеется функция нескольких переменных При Будем рассматривать только такие функции, которые обращаются в нуль в начале координат, то есть при
Кроме того, Функция
Для
Функция Пример для
Обращается в нуль на прямой Функция Для
53. Функция Ляпунова и её производная по времени Нелинейная система может быть описана системой нелинейных уравнений:
где
Любая функция
называется функцией Ляпунова, если в качестве переменных Производная по времени функции Ляпунова имеет вид
Подставим в (28.4) выражения
Следовательно,
Таким образом, Теорема Ляпунова. Если при заданных в форме (28.1) уравнениях нелинейной системы n -го порядка можно подобрать такую знакоопределенную функцию Пример. Пусть задана нелинейная САУ, которая описывается системой уравнений:
Выберем функцию Ляпунова в виде:
V > 0 при любых xi, а,b,c – произвольные вещественные числа. Будем придавать этой функции постоянные значения 0,С1,С2,…., причем 0<С1<С2 … Тогда получим
Возьмем производную от V по времени
Если полученная функция
то V убывает во всех точках пространства, кроме начала координат,
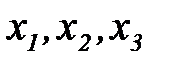 уменьшаются, то есть система устойчива. уменьшаются, то есть система устойчива.
При практическом применении метода наибольшую трудность вызывает подбор функции V, так как эта задача неоднозначна и не существует формальных методов нахождения V, поэтому приходится полагаться на опыт и интуицию и подбор вариантов. Однако, несмотря на это, метод применяется не только для исследования нелинейных систем, но и при анализе и синтезе адаптивных законов управления. Адаптивные системы управления относятся к классу нелинейных систем.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.23.149 (0.009 с.) |

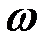 и
и 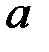 , поэтому задачу решают графически.
, поэтому задачу решают графически.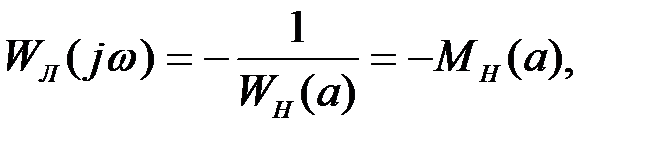 (27.18)
(27.18) – обратный комплексный коэффициент передачи НЗ, который равен
– обратный комплексный коэффициент передачи НЗ, который равен . (27.19)
. (27.19)
 .
.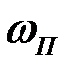 определяют из годографа линейной части
определяют из годографа линейной части  , а значение амплитуды
, а значение амплитуды  определяется из годографа
определяется из годографа 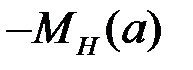 .
. . (27.20)
. (27.20)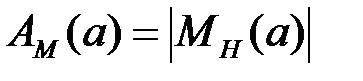 – модуль передачи нелинейного элемента,
– модуль передачи нелинейного элемента, .
. , (27.21)
, (27.21) ; где m = 0, ±1, ±2,…
; где m = 0, ±1, ±2,…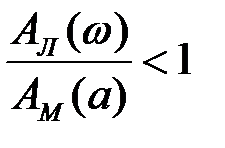 , значит
, значит  и в соответствии с критерием Найквиста система устойчива, поэтому в ней будут затухающие колебания.
и в соответствии с критерием Найквиста система устойчива, поэтому в ней будут затухающие колебания.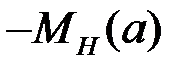 лежит в области D 1, то система будет неустойчива, и в ней будут существовать расходящиеся колебания.
лежит в области D 1, то система будет неустойчива, и в ней будут существовать расходящиеся колебания. – амплитуда – (а п + ∆a); в точке
– амплитуда – (а п + ∆a); в точке 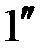 – амплитуда – (а п – ∆a).
– амплитуда – (а п – ∆a). не охватывает точку на годографе
не охватывает точку на годографе 

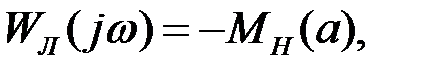

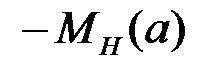 . Комплексный коэффициент передачи нелинейного звена будет равен
. Комплексный коэффициент передачи нелинейного звена будет равен ,
,

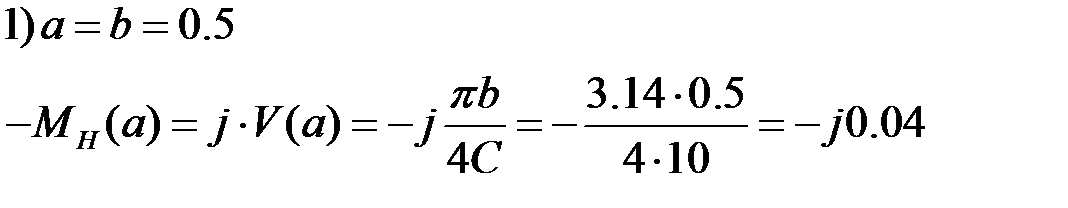 .
.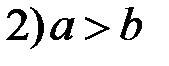


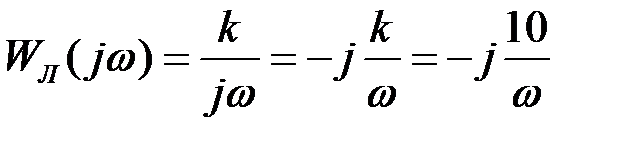
 построены на рис. 27.17.
построены на рис. 27.17.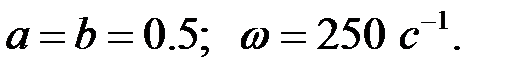
 .
.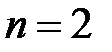 эта функция может быть изображена на фазовой плоскости, при
эта функция может быть изображена на фазовой плоскости, при 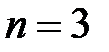 – в трехмерном пространстве. В каждой точке пространства функция
– в трехмерном пространстве. В каждой точке пространства функция 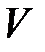 имеет определенное значение.
имеет определенное значение. ,
,  .
. .
. .
.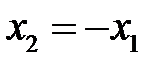 и
и  .
.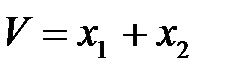 .
.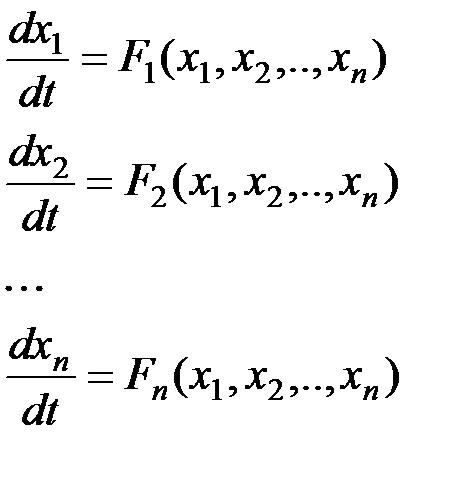 (28.1)
(28.1) – переменные состояния системы.
– переменные состояния системы. (28.2)
(28.2) (28.4)
(28.4)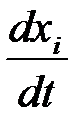

 (28.5)
(28.5) (28.6)
(28.6) является функцией переменных состояния. Причем, согласно свойства (28.2),
является функцией переменных состояния. Причем, согласно свойства (28.2), 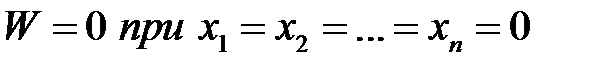 . Поэтому к этой функции можно применить понятие знакоопределенной, знакопостоянной и знакопеременной функции.
. Поэтому к этой функции можно применить понятие знакоопределенной, знакопостоянной и знакопеременной функции. также была знакоопределенной или знакопостоянной, но имела знак, противоположный знаку функции V, то данная система устойчива.
также была знакоопределенной или знакопостоянной, но имела знак, противоположный знаку функции V, то данная система устойчива.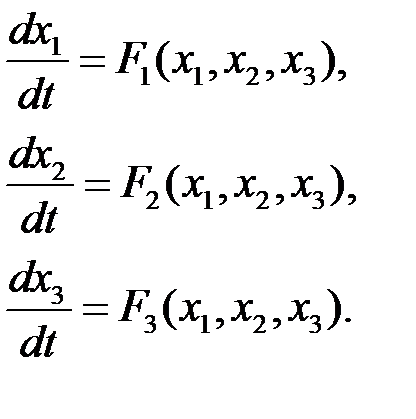 (28.7)
(28.7) , (28.8)
, (28.8)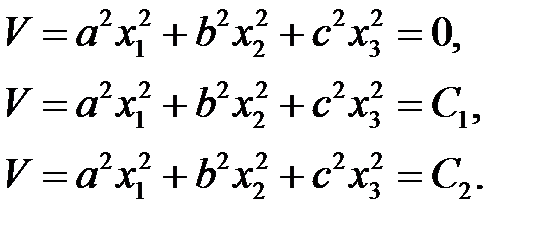 (28.9)
(28.9)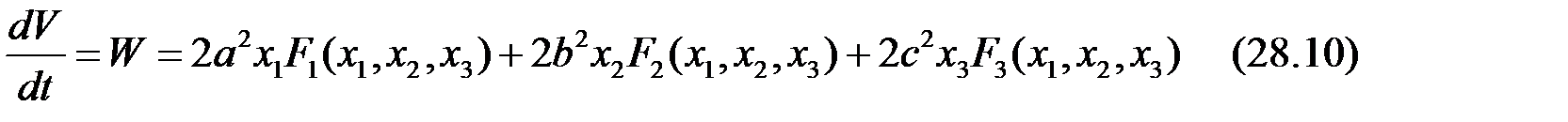
 является знакоопределенной отрицательной, то есть
является знакоопределенной отрицательной, то есть



