
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический смысл функционирования системыСодержание книги
Поиск на нашем сайте
Система должна работать так, чтобы величина ошибки была равна нулю. Это условие выполняется, если G(t)= Y(t). Математическое описание исходных данных 1.Элементы моделируемой системы
2. Описание входных сигналов По каналу передачи управляющего воздействия:
По каналу передачи возмущающего воздействия:
3. Разностное уравнение дискретного ПИ регулятора: Для программирования данной системы необходимо перейти от дискретных функций элементов системы к разностным уравнениям. Получим разностное уравнение для ПИ – регулятора: Делим на высшую степень z: Определение дискретной модели заданной непрерывной части системы и соответствующего разностного уравнения. Дискретная передаточная функция канала управления:
Разностное уравнение для канала управления:
Делим на высшую степень z:
Описание непрерывной и дискретной модели нелинейного элемента регулирующего органа. В моделируемой системе нелинейная характеристика присутствует в регулирующем органе. Вид нелинейности – «зона нечувствительности с ограничениями».
Вид нелинейности - «зона нечувствительности с ограничениями» Входом нелинейного элемента является S(t)-сигнал с выхода исполнительного механизма. Выходом – переменная нелинейного элемента U(t)-сигнал с выхода регулирующего органа.
Переходим к дискретной форме записи
Составление системы уравнений, описывающих работу замкнутой системы управления.
Для текущего такта [n] > 0 система уравнений примет следующий вид:
(1) (2) (3) (4) (5) (6) (7) (8) (9) Анализ полученной системы уравнений для определения типа переменных и способа их хранения: 1) Для переменных x[n],U[n],R[n] и Y0[n] в расчётах используются как текущее, так и предыдущие значения, отсюда следует, что необходимо определить их как нумерованные массивы данных. Член массива с отрицательным индексом автоматически будет приравнен к нулю.
2)Переменная Y1[n] является переменной с предыдущим значением. 3) Все остальные переменные – простые переменные.
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.215 (0.007 с.) |

 -дискретный ПИ регулятор;
-дискретный ПИ регулятор; -передаточная функция формирующего элемента;
-передаточная функция формирующего элемента; -коэффициент передачи исполнительного механизма;
-коэффициент передачи исполнительного механизма; - коэффициент передачи регулирующего органа;
- коэффициент передачи регулирующего органа; - коэффициент передачи датчика;
- коэффициент передачи датчика; - передаточная функция канала управления;
- передаточная функция канала управления; - задающее воздействие;
- задающее воздействие; - передаточная функция по каналу возмущения;
- передаточная функция по каналу возмущения; - сигнал возмущения;
- сигнал возмущения;





 ;
; ;
;
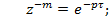








 ;
; ;
; ;
;









 ;
;





