
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность и методы эффективного кодирования.Содержание книги Поиск на нашем сайте
Под кодированием будем понимать отображение состояний некоторой системы (источника сообщений) с помощью состояний сложного сигнала, который представляет собой последовательность из n элементарных сигналов. Множество Y состояний элементарного сигнала образует алфавит кода размера mу. При my=2 элементарный сигнал имеет два состояния, которые обозначим через 1 и 0. Состояние сложного сигнала описывается последовательностью из нулей и единиц, которая называется кодовым словом. Если кодовые слова имеют разную длину, то код называется неравномерным, а если одинаковую, то код называется равномерным. Пусть источник сообщений вырабатывает последовательность из k букв, причем xi буква в этой последовательности появляется n раз. Каждой букве xi (i= Это равенство можно представить в виде При неограниченном увеличении числа букв К в последовательности относительная частота появления х{ буквы с вероятностью, равной единице, совпадает со значением вероятности pi появления этой буквы. Поэтому с вероятностью, равной единице, выполняется равенство
Таким образом, источник сообщений с вероятностью, равной единице, вырабатывает типичные последовательности, длина которых мало отличается от их среднего значения К Поскольку время передачи сообщений определяется длиной L, то имеется возможность его сокращения за счет уменьшения средней длины кодового слова
Для уменьшения избыточности символов необходимо применить эффективное кодирование. Эффективным называется способ кодирования, при котором: 1. Не возникает потери информации. 2. Требуется минимальное количество кодовых символов. Для выполнения второго условия используются неравномерные коды, где длина кодового слова обратно пропорциональна вероятности его появления в сообщении. Использование эффективного кодирования целесообразно, если вероятности появления различных букв существенно различаются, так как при этом энтропия множества букв (блоков) существенно меньше их информационной емкости. Эффективное кодирование достигается благодаря учету априорных статистических характеристик источника информации. Предельные возможности эффективного кодирования определяются
Алгоритмы эффективного кодирования Алгоритм Шеннона-Фано.
Пусть имеется множество сообщений 1. Все сообщения располагаются в порядке убывания их вероятностей. 2. Упорядоченное множество сообщений делится на две части: верхнюю часть и нижнюю часть, причем так, чтобы разность между суммой вероятностей в верхней и нижней части была минимальной. 3. После этого сообщениям в верхней части ставится в соответствие 1, а в нижней – 0. 4. Далее аналогичные действия производятся с каждой из частей. Вновь полученные подмножества сообщений снова аналогичным образом делятся на две части и т.д., до получения по одному сообщению в каждом из подмножеств. 5. В результате каждому сообщению будет соответствовать своя последовательность из нулей и единиц, т.е. кодовое слово.
Пример:
Алгоритм Хаффмена.
1. Все сообщения располагаются в порядке убывания их вероятностей. 2. Два самых нижних сообщения объединяются в одно событие, вероятность которого равна сумме вероятностей, объединяемых событий, причем верхнему событию ставится в соответствие 1, а нижнему 0. 3. Получился новый массив сообщений с количеством состояний на единицу меньшим по сравнению с предыдущим массивом, если два последних события считать одним более крупным событием. Далее преобразуем этот массив в соответствии с пунктами 1 и 2. Полученный массив вновь подвергаем указанным преобразованиям и т.д. до тех пор, пока не будет исчерпан весь массив. 4. Геометрически результат можно представить в виде дерева, где кодовое слово, соответствующее
Пример:
x1=1, x2 = 01, x3 = 001, x4 = 000
б)Эпсилон-Энтропия. Производительность источника с непрерывным множеством состояний. ЭПСИЛОН - ЭНТРОПИЯ Проблема передачи непрерывного сообщения заключается в получении его копии на приемном пункте и, в сущности, сводится к процедуре воспроизведения сообщения на основе полученной информации. Очевидно, в данном случае не существует способа, позволяющего получить точную копию передаваемого сообщения, поскольку это требует бесконечной точности его воспроизведения, причем неограниченное увеличение точности требует неограниченного увеличения количества передаваемой информации. Например, нельзя получить два абсолютно совпадающих графика. Поэтому о передаче непрерывного сообщения имеет смысл говорить только в том случае, когда задана точность его воспроизведения. Передача непрерывного сообщения Пусть случайная величина Количество взаимной информации между множествами
равно энтропии Пронумеруем все элементы множества
Если величина Более универсальной мерой точности воспроизведения по сравнению с
которую при неравномерном распределении случайной величины Таким образом, количество информации, которое требуется для воспроизведения значения случайной величины Определим e - энтропию как минимальное по
Следует напомнить, что пропускная способность канала При квантовании непрерывной величины Отметим, что e - энтропия также используется и в качестве количественной меры производительности источника непрерывных сообщений, при этом, очевидно, нельзя говорить о производительности источника не задав точность воспроизведения. Таким образом, производительность источника можно определить как минимальное количество информации Кроме квантования существует много других способов преобразования непрерывной величины
где
Билет 11. Билет (сделала 2 варианта первого вопроса – по лекциям Ломакина и по методичке)
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1024; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.250.187 (0.007 с.) |

 ) поставим в соответствие кодовое слово с длиной, равной li (посимвольное кодирование). Тогда длина соответствующей последовательности из кодовых слов будет равна
) поставим в соответствие кодовое слово с длиной, равной li (посимвольное кодирование). Тогда длина соответствующей последовательности из кодовых слов будет равна 


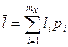 - по определению средняя длина кодового слова. Длина последовательности кодовых слов L является случайной величиной, но значительные отклонения ее от среднего значения
- по определению средняя длина кодового слова. Длина последовательности кодовых слов L является случайной величиной, но значительные отклонения ее от среднего значения  =К
=К  маловероятны при неограниченном возрастании K.
маловероятны при неограниченном возрастании K. ). Задача оптимального кодирования заключается в определении однозначно декодируемых кодовых слов с такими длинами, при которых их средняя длина минимальна.
). Задача оптимального кодирования заключается в определении однозначно декодируемых кодовых слов с такими длинами, при которых их средняя длина минимальна.
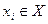 .
. выражается последовательностью дерева с соответствующим сообщением
выражается последовательностью дерева с соответствующим сообщением 
 сводится к передаче последовательности его значений взятых в дискретные моменты времени. Все возможные значения функции
сводится к передаче последовательности его значений взятых в дискретные моменты времени. Все возможные значения функции  .
. распределение. Тогда распределение дискретной случайной величины
распределение. Тогда распределение дискретной случайной величины 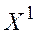 также будет равномерным, если все интервалы на которые разбит отрезок
также будет равномерным, если все интервалы на которые разбит отрезок  достигает своего максимального значения, равного
достигает своего максимального значения, равного  , где
, где  - число элементов в множестве
- число элементов в множестве  ,
, , с которой значение случайной величины
, с которой значение случайной величины  требуется количество информации, равное
требуется количество информации, равное  - ичной системе счисления. Минимальное количество разрядов
- ичной системе счисления. Минимальное количество разрядов 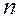 , некоторое при этом потребуется, удовлетворяет неравенству:
, некоторое при этом потребуется, удовлетворяет неравенству: .
. окажется целым числом, то количество информации, необходимое для воспроизведения значения случайной величины
окажется целым числом, то количество информации, необходимое для воспроизведения значения случайной величины 
 и их количество. Канал, устанавливающий связь между множествами
и их количество. Канал, устанавливающий связь между множествами  и, в сущности, представляет собой устройство квантования.
и, в сущности, представляет собой устройство квантования. источника:
источника:

 была определена как максимальное количество взаимной информации, но не по
была определена как максимальное количество взаимной информации, но не по  , то передача информации в виде чисел, записанных в
, то передача информации в виде чисел, записанных в  , не будет экономной. Поэтому целесообразно предварительно осуществить экономное кодирование сообщений, в роли которых должны выступать элементы множества
, не будет экономной. Поэтому целесообразно предварительно осуществить экономное кодирование сообщений, в роли которых должны выступать элементы множества  , необходимое в единицу времени для воспроизведения непрерывного сообщения
, необходимое в единицу времени для воспроизведения непрерывного сообщения  . Тогда при заданной дисперсии
. Тогда при заданной дисперсии  погрешности (при заданной среднеквадратичной ошибке) e - энтропия нормальной величины
погрешности (при заданной среднеквадратичной ошибке) e - энтропия нормальной величины  ,
, - дисперсия случайной величины
- дисперсия случайной величины 


