Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя путевая и средняя скорость перемещения. Мгновенная линейная скорость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тангенциальное ускорение. Направление вектора тангенциального ускорения Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 10. Вектор углового перемещения и угловая скорость. Прямая и обратная связь угловой скорости и вектора углового перемещения.
Угловое ускорение. Прямая и обратная связь угловой скорости и вектора углового перемещения. Угловое ускорение, величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, когда его угловая скорость w растет (или убывает) равномерно, численно У. у. e = Dw/Dt, где Dw — приращение, которое получает w за промежуток времени Dt, а в общем случае при вращении вокруг неподвижной оси e = dw/dt = d 2j/dt2, где j — угол поворота тела. Вектор У. у. e направлен вдоль оси вращения (в сторону w при ускоренном вращении и противоположно w — при замедленном). При вращении вокруг неподвижной точки вектор У. у. определяется как первая производная от вектора угловой скорости w по времени, т. е. e = dw/dt, и направлен по касательной к годографу вектора w в соответствующей его точке. Размерность У. у. Т-2. Масса тела и ее свойства. Центр масс системы. Отношение величины силы, действующей на тело, к приобретенному телом ускорению постоянно для данного тела. Масса тела и есть это отношение.
Масса тела является неизменной характеристикой данного тела, не зависящей от его местоположения. Масса характеризует два свойства тела: Инерция Тело изменяет состояние своего движения только под воздействием внешней силы. Тяготение Между телами действуют силы гравитационного притяжения. Эти свойства присущи не только телам, т.е. веществу, но и другим формам существования материи (например излучению, полям). Справедливо следующее утверждение: Масса тела характеризует свойство любого вида материи быть инертной и тяжелой, т.е. принимать участие в гравитационных взаимодействиях. Центр масс и система центра масс В любой системе частиц имеется одна замечательная точка С- центр инерции, или центр масс, - которая обладает рядом интересных и важных свойств. Центр масс является точкой приложения вектора импульса системы
где системы (рис. 4.3).
Фундаментальные и нефундаментальные взаимодействия. Сила как мера взаимодействия тел. Свойства силы. Фундамента́льные взаимоде́йствия — качественно различающиеся типы взаимодействия элементарных частиц и составленных из них тел. На сегодня достоверно известно существование четырех фундаментальных взаимодействий: - гравитационного - электромагнитного - сильного - слабого При этом электромагнитное и слабое взаимодействия являются проявлениями единого электрослабого взаимодействия.
Первый закон Ньютона Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Или Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно. 18. Второй закон Ньютона Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). Современная формулировка
где Или в более известном виде:
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
где
Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:
или
Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности. Нельзя рассматривать частный случай (при 19. Третий закон Ньютона Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой Современная формулировка
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами. Сила трения покоя
Рассмотрим взаимодействие бруска с поверхностью стола. Поверхность соприкасающихся тел не является абсолютно ровной. Наибольшая сила притяжения возникает между атомами веществ, находящимися на минимальном расстоянии друг от друга, т.е. на микроскопических выступах. Суммарная сила притяжения атомов соприкасающихся тел столь значительна, что даже под действием внешней силы F, приложенной к бруску параллельно поверхности его соприкосновения со столом, брусок остается в покое. Это означает, что на брусок действует сила, равная по модулю внешней силе, но противоположно направленная. Эта сила является силой трения покоя.
Когда приложенная сила достигает максимального критического значения (Fтр.п)max достаточного для разрыва связей между выступами, брусок начинает скользить по столу. Естественно предположить, что (Fтр.п)max пропорциональна числу n взаимдействующих выступов и давлению p бруска на стол: (Fтр.п)max~np. Давление равно отношению силы нормального давления, действующей перпендикулярно поверхности соприкосновения тел, к площади поверхности S: p=F/S Число взаимодействующих выступов пропорционально площади поверхности соприкосновения тел: n~S, поэтому (Fтр.п)max~S*F/S~F+.
По третьему закону Ньютона сила нормального давления равна по модулю силе нормальной реакции опоры N. Максимальная сила трения покоя (Fтр.п)max пропорциональна силе нормального давления: (Fтр.п)max=mпN
Коэффициент трения покоя зависит от характера обработки поверхности и от сочетания материалов, из которых состоят соприкасающиеся тела. Качественная обработка гладких поверхностей контакта приводит к увеличению числа притягивающихся атомов и соответственно к увеличению коэффициента трения покоя. Силы притяжения отдельных атомов различных веществ существенно зависят от их электрических свойств. Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя. Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным. величина силы трения скольжения может быть рассчитана по формуле:
Сила трения качения - сила трения, возникающая при качении одного тела по поверхности другого тела тре́ние каче́ния — сопротивление движению, возникающее при перекатывании тел друг по другу. Проявляется, например, между элементами подшипников качения, между шиной колеса автомобиля и дорожным полотном. В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике. Трение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.
f — коэффициент трения качения, имеющий размерность длины (следует отметить важное отличие от коэффициента трения скольжения, который безразмерен); R — радиус катящегося тела; N — прижимающая сила. Средняя путевая и средняя скорость перемещения. Мгновенная линейная скорость. Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:
Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной. Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени. В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути. Средняя скорость по перемещению Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:
Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение). Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению. Мгновенная скорость - предел средней скорости за бесконечно малый промежуток времени. Мгновенная скорость направлена по касательной к траектории движения в данной точке траектории. Средняя скорость перемещения равна отношению полного перемещения к промежутку времени, за которое это перемещение совершено.
где Средняя путевая скорость равна отношению полного пути к промежутку времени, за который этот путь пройден.
где υср - средняя путевая скорость, l - путь. Мгновенная скорость - скорость в заданный момент времени.
7. Прямая и обратная связь мгновенной линейной скорости и радиуса-вектора материальной точки, модуля скорости и пройденного пути. 8. Линейное ускорение. Прямая и обратная связь линейного ускорения и мгновенной линейной скорости. Линейным ускорением называют отношение изменения величины скорости ко времени, в течение которого это изменение произошло. Видами движений с линейным ускорением являются разгон и торможение автомобиля, взлет самолета, разбег человека при прыжке и т. д. 9. Ускорение при криволинейном движении материальной точки. Тангенциальное и нормальное ускорение. Ускорение при криволинейном движении материальной точки В механике вводится еще одна важная характеристика движения – ускорение, т.е. скорость изменения вектора скорости
Учитывая определение скорости
Особенно удобен естественный способ представления ускорения.
В общем случае криволинейного движения ускорение
Эти две составляющие ускорения имеют специальные названия:
Рассматривая криволинейное движение тела, мы видим, что его скорость в разные моменты различна. Даже в том случае, когда величина скорости не меняется, все же имеет место изменение направления скорости. В общем случае меняются и величина, и направление скорости.
Рис. 49. Изменение скорости при криволинейном движении. Таким образом, в криволинейном движении всегда имеется изменение скорости, т. е. это движение происходит с ускорением. Для определения этого ускорения (по величине и направлению) требуется найти изменение скорости как вектора, т. е. требуется найти изменение величины и изменение направления скорости. Пусть, например, точка, двигаясь криволинейно (рис. 49), имела в некоторый момент скорость v1 а через малый промежуток времени — скорость v2. Изменение скорости есть разность между векторами v1 и v2. Так как эти векторы имеют различное направление, то нужно взять их векторную разность. Изменение скорости выразится вектором w, изображаемым стороной параллелограмма с диагональю v2 и другой стороной v1. Ускорением мы называем отношение изменения скорости к промежутку времени, за который это изменение произошло. Значит, ускорение а равно
и по направлению совпадает с вектором w. Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Тангенциальное ускорение. Направление вектора тангенциального ускорения Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 10. Вектор углового перемещения и угловая скорость. Прямая и обратная связь угловой скорости и вектора углового перемещения.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1961; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

 , так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:
, так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:
 - масса и радиус-вектор каждой частицы системы, M - масса всей
- масса и радиус-вектор каждой частицы системы, M - масса всей

 — ускорение материальной точки;
— ускорение материальной точки; — сила, приложенная к материальной точке;
— сила, приложенная к материальной точке; — масса материальной точки.
— масса материальной точки.

 — импульс точки,
— импульс точки,
 — скорость точки;
— скорость точки; — время;
— время; — производная импульса по времени.
— производная импульса по времени.

 ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО. , а второе — на первое с силой
, а второе — на первое с силой 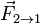 . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.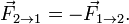
 Трение покоя - трение, возникающее при отсутствии относительного перемещения соприкасающихся тел.
Трение покоя - трение, возникающее при отсутствии относительного перемещения соприкасающихся тел.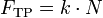 , где
, где — коэффициент трения скольжения,
— коэффициент трения скольжения, — сила нормальной реакции опоры.
— сила нормальной реакции опоры. где
где — сила трения качения;
— сила трения качения;


 ср -средняя скорость перемещения,
ср -средняя скорость перемещения,  - перемещение, ∆ t -интервал времени.
- перемещение, ∆ t -интервал времени.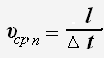

 во времени:
во времени: - ускорение при криволинейном движении материальной точки.
- ускорение при криволинейном движении материальной точки. есть вторая производная от радиус-вектора
есть вторая производная от радиус-вектора  по времени t (две точки означают вторую производную по времени t). Легко установить связь с координатным представлением ускорения:
по времени t (две точки означают вторую производную по времени t). Легко установить связь с координатным представлением ускорения: - модуль вектора ускорения.
- модуль вектора ускорения.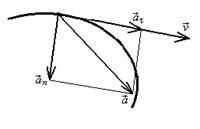
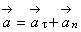 .
. – тангенциальное ускорение,
– тангенциальное ускорение, 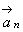 - нормальное ускорение.
- нормальное ускорение.