Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм симплексного методаСодержание книги Поиск на нашем сайте
1. Математическая модель задачи должна быть канонической. Если она неканоническая, то ее надо привести к каноническому виду. 2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплексную таблицу (табл. 21.1). Все строки таблицы 1-го шага, за исключением строки Δ j (индексная строка), заполняем по данным системы ограничений и целевой функции.
Индексная строка для переменных находится по формуле
и по формуле
Возможны следующие случаи при решении задачи на максимум: — если все оценки Δ j ≥ 0, то найденное решение оптимальное; — если хотя бы одна оценка Δ j ≤ 0, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращаем, так как L() → — если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению; — если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка. Если хотя бы одна оценка Δ k < 0, то k- й столбец принимаем за ключевой. За ключевую строку принимаем ту, которой соответствует минимальное отношение свободных членов (bi) к положительным коэффициентам k- гo столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называется ключевым элементом. 3. Заполняем симплексную таблицу 2-го шага: — переписываем ключевую строку, разделив ее на ключевой элемент; — заполняем базисные столбцы; — остальные коэффициенты таблицы находим по правилу "прямоугольника"*. Оценки можно считать по приведенным выше формулам или по правилу "прямоугольника" Получаем новое опорное решение, которое проверяем на оптимальность, и т.д.
81. Решение задачи оптимизации выпуска продукции симплекс-методом Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в табл. 21.2 (в усл. ед.).
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором — 4 тыс. изделий. Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции? Решение. Составим математическую модель задачи. Обозначим: x 1 — время работы предприятия первым способом, x 2 — время работы предприятия вторым способом. Математическая модель имеет вид
при ограничениях:
Приведем задачу к каноническому виду:
при ограничениях:
Составляем симплексную таблицу 1-го шага (табл. 21.3).
Получим решение:
В индексной строке Δ j имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменной х 2, а за ключевую строку взять строку переменной x 3, где min (4/2,3/l, 8/1) = min (2, 3, 8) = 2. Ключевым элементом является (2). Вводим в столбец базисной переменной х 2, выводим х 3. Составляем симплексную таблицу 2-го шага (табл. 21.4). Получим
В индексной строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является (1/2). Составляем симплексную таблицу 3-го шага (табл. 21.5).
Все оценки свободных переменных Δ j ≥ 0, следовательно, найденное опорное решение является оптимальным:
Таким образом, по первому способу предприятие должно работать два месяца, по второму — один месяц, при этом максимальный выпуск продукции составит 10 тыс. ед.
82. Модель оптимизации плана перевозок (транспортная задача). Экономическая постановка задачи. Транспортная задача — одна из распространенных задач линейного программирования. Ее цель — разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д. В общем виде задачу можно представить следующим образом: в т. пунктах производства A 1, A 2,..., Am имеется однородный груз в количестве соответственно a 1, a 2 ,…, am. Этот груз необходимо доставить в п пунктов назначения B 1, В 2, …., Вп в количестве соответственно b 1, b 2 ,..., bп. Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна cij. Требуется составить план перевозок, позволяющий вывезти все грузы и имеющий минимальную стоимость. В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми. Определение 1. Если
то задача называется закрытой. Если
то открытой. Обозначим через xij количество груза, перевозимого из пункта Ai в пункт Bj. Рассмотрим закрытую транспортную задачу. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения (табл. 23.1).
Математическая модель закрытой транспортной задачи имеет вид
при ограничениях:
Оптимальным решением задачи является матрица
удовлетворяющая системе ограничений и доставляющая минимум целевой функции. Транспортная задача как задача линейного программирования может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно: — нахождение исходного опорного решения; — проверка этого решения на оптимальность; — переход от одного опорного решения к другому.
83. Математическая модель транспортной задачи. Открытые и закрытые задачи. Допустимый, опорный и оптимальный планы перевозок. ≈82.
84. Построение начального (опорного) плана перевозок по методу северо-западного угла и по методу наименьшей стоимости.
87. Понятия испытания и случайного события. Частота и относительная частота появления события в серии испытаний. Вероятность случайного события. События, происходящие в окружающем нас мире, можно разделить на три вида: достоверные, невозможные и случайные. Достоверным относительно комплекса условий S называется событие, которое обязательно произойдет при осуществлении этого комплекса условий. Например, если гладкий желоб с лежащим внутри него тяжелым шариком наклонить, то шарик обязательно покатится по желобу в сторону уклона. Невозможным называется событие, которое заведомо не произойдет при осуществлении комлекса условий S. Например, из герметически изолированного сосуда вода не может вылиться. Случайным относительно комплекса условий S называется событие, которое при осуществлении указанного комплекса условий может либо произойти, либо не произойти. Например, если вы уронили фарфоровую чашку на пол, то она может как разбиться, так и остаться неповрежденной. Теория вероятностей имеет дело со случайными событиями. Однако она не может предсказать, произойдет единичное событие или нет. Теория вероятностей изучает вероятностные закономерности массовых однородных случайных событий. Ее методы получили широкое распространение в различных областях естествознания и в прикладных проблемах техники. Теория вероятностей легла в основу теории массового обслуживания и теории надежности. В последние годы аппарат теории вероятностей активно используется в экономике. Выше было введено определение случайного события. Обычно в теории вероятностей вместо "совокупности условий" употребляют термин "испытание", и тогда событие трактуется как результат испытания. Например, стрельба по мишени: выстрел — это испытание, попадание в мишень — это событие. Другой пример: подбрасывание монеты вверх — это испытание, выпадение орла (или решки) — это событие. Определение 1. События называют несовместными, если в одном и том же испытании появление одного из них исключает появление других. Например, выпадение орла при подбрасывании монеты исключает появление в этом же испытании решки и наоборот. Определение 2. Несколько событий образуют полную группу, если в результате испытания появление хотя бы одного из них является достоверным событием. Например, при произведении выстрела по мишени (испытание) обязательно будет либо попадание, либо промах; эти два события образуют полную группу. Следствие. Если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай будет использован далее.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.27.153 (0.007 с.) |



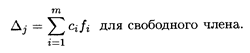
 , т.е. целевая функция неограничена в области допустимых решений;
, т.е. целевая функция неограничена в области допустимых решений;