
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторовСодержание книги
Поиск на нашем сайте Определение. Скалярным произведением векторов
Формально такое определение скалярного произведения двух векторов согласуется с аналогичной величиной для двух- и трехмерных векторов. Из данного определения следуют основные свойства скалярного произведения векторов: 1. 2. 3. 4.
Определение. Линейное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее свойствам 1-4, называется евклидовым. Определение. Для векторов из
Необходимое условие для последней формулы, что
Векторы
Линейная зависимость векторов Линейно зависимые и линейно независимые системы векторов При решении различных задач, как правило, приходится иметь дело не с одним вектором, а с некоторой совокупностью векторов одной и той же размерности. Такие совокупности называют системой векторов и обозначают
Определение. Линейной комбинацией векторов называется вектор вида
где Например, пусть даны три вектора:
Определение. Множество всевозможных линейных комбинаций системы векторов Определение. Система ненулевых векторов
Если же последнее равенство для данной системы векторов возможно лишь при Например, система двух векторов Пусть система векторов (19) линейно зависима. Выберем в сумме (20) слагаемое, в котором коэффициент
Как видно из этого равенства, один из векторов линейно зависимой системы (19) оказался выраженным через другие векторы этой системы (или разлагается по остальным ее векторам). Свойства линейно зависимой системы векторов 1. Система, состоящая из одного ненулевого вектора, линейно независима. 2. Система, содержащая нулевой вектор, всегда линейно зависима. 3. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди ее векторов содержится, по крайней мере, один вектор, который линейно выражается через остальные.
Геометрический смысл линейной зависимости в случае двухмерных векторов на плоскости: когда один вектор выражается через другой, мы имеем В пространственном случае линейной зависимости трех векторов они параллельны одной плоскости, т.е. компланарны. Достаточно «подправить» соответствующими сомножителями длины этих векторов, чтобы один из них стал суммой двух других или выражался через них.
Теорема. В пространстве Пример. Выяснить, являются ли векторы Решение. Составим векторное равенство
Таким образом, задача свелась к решению системы
Решим систему методом Гаусса:
В результате получим систему уравнений:
которая имеет бесконечное множество решений, среди которых обязательно найдется одно ненулевое, следовательно, векторы
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 и
и 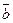 называется число, состоящее из суммы произведений соответствующих координат этих векторов:
называется число, состоящее из суммы произведений соответствующих координат этих векторов:
 .
. .
. .
. , если
, если  и
и 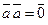 , если
, если 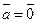 .
. -мерного пространства модуль вектора
-мерного пространства модуль вектора 
 .
. , гарантируется неравенством Коши-Буняковского, справедливым для любых двух векторов
, гарантируется неравенством Коши-Буняковского, справедливым для любых двух векторов  .
. .
. (18)
(18)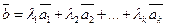 (19)
(19) - любые действительные числа. Также говорят, что вектор
- любые действительные числа. Также говорят, что вектор  ,
,  ,
,  . Их линейной комбинацией с коэффициентами соответственно 2, 3 и 4 является вектор
. Их линейной комбинацией с коэффициентами соответственно 2, 3 и 4 является вектор .
. (20)
(20) , то эта система векторов называется линейно независимой.
, то эта система векторов называется линейно независимой. ,
,  линейно независима; система двух векторов
линейно независима; система двух векторов  и
и  линейно зависима, так как
линейно зависима, так как  .
. , и выразим его через остальные слагаемые:
, и выразим его через остальные слагаемые: .
. , т.е. эти векторы коллинеарны, или что то же самое, находятся на параллельных прямых.
, т.е. эти векторы коллинеарны, или что то же самое, находятся на параллельных прямых.
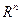 любая система, содержащая
любая система, содержащая  векторов, линейно зависима при
векторов, линейно зависима при  .
.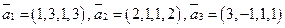 линейно зависимыми.
линейно зависимыми. . Записывая
. Записывая  в виде вектор-столбцов, получаем
в виде вектор-столбцов, получаем .
.

 ,
,


