
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Аналитическая геометрия на плоскости.Содержание книги
Поиск на нашем сайте
Уравнение линии на плоскости Пусть на плоскости задана система. Рассмотрим уравнение вида
Это равенство называется уравнением некоторой линии L в заданной системе координат. Вообще говоря, линии на координатной плоскости могут быть самыми различными. Линии первого порядка
К линиям первого порядка относятся те линии, для которых задающее их уравнение (63) содержит переменные
где А, В и С – постоянные числа. Из этого уравнения можно выразить переменную
Уравнение (65) называют уравнением прямой с угловым коэффициентом Уравнение прямой с заданным угловым коэффициентом
Уравнение прямой, проходящей через две заданные точки на плоскости
Тогда
Формула (68) определяет один из углов между пересекающимися прямыми; второй угол равен Из равенства (68) вытекают условия параллельности и перпендикулярности прямых. Если прямые параллельны, то Если прямые перпендикулярны, то Пример. Найти угол между заданными прямыми Решение.
откуда один из углов равен
5.2. Линии второго порядка. Рассмотрим три наиболее используемых вида линий: эллипс, гиперболу и параболу. 5.2.1 Эллипс. Определение. Линия, для всех точек которой сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами, называется эллипсом.
Точки Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет - величина, определяемая отношением
Очевидно, что Согласно определению эллипса сумма расстояний от произвольной точки
Отсюда можно вывести уравнение эллипса в его основной (канонической) форме
где Из уравнения (70) следует, что оси эллипса являются осями его симметрии, а точка их пересечения – центром его симметрии. В частном случае, когда Пример. Определить вид и расположение кривой
Решение. Дополним члены, содержащие
Следовательно, заданная кривая представляет эллипс с полуосями
Гипербола Определение. Гиперболой называется линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Разность расстояний от произвольной точки
Из этой основной предпосылки выводится каноническое уравнение гиперболы, которое имеет вид:
где Нетрудно видеть, что прямые Фокусы гиперболы -
Парабола Определение. Параболой называется линия, все точки которой находятся на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Согласно определению точка
Точка
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.01 с.) |

 (63)
(63)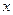 и
и  только в первой степени, т.е. такие линии описываются уравнениями вида
только в первой степени, т.е. такие линии описываются уравнениями вида (64)
(64) :
:
 (65)
(65) , где j - угол наклона прямой к положительному направлению оси
, где j - угол наклона прямой к положительному направлению оси  . Если
. Если  , то прямая параллельна оси
, то прямая параллельна оси  масштабных единиц.
масштабных единиц. , проходящей через заданную точку:
, проходящей через заданную точку: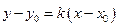 (66)
(66) и
и  :
: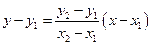 (67)
(67) Угол между двумя прямыми. Рассмотрим две прямые, заданные уравнениями
Угол между двумя прямыми. Рассмотрим две прямые, заданные уравнениями 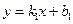 и
и  , где
, где  и
и  . Пусть j - угол между этими прямыми.
. Пусть j - угол между этими прямыми. и получаем:
и получаем:  или, что то же самое,
или, что то же самое, (68)
(68) .
. .
. , откуда
, откуда  или
или  .
. и
и  .
. ,
,  , подставляя эти значения в формулу (68), получаем:
, подставляя эти значения в формулу (68), получаем:
 .
. Расстояние от точки до прямой. Пусть прямая задана уравнением общего вида (64). Тогда расстояние
Расстояние от точки до прямой. Пусть прямая задана уравнением общего вида (64). Тогда расстояние  от произвольной точки
от произвольной точки  до прямой задается формулой
до прямой задается формулой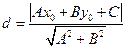 (69)
(69)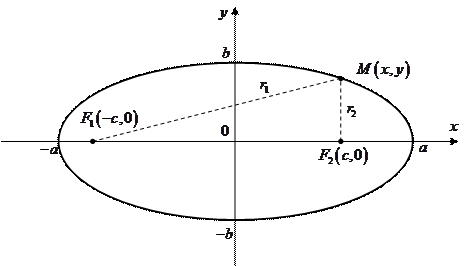
 и
и  , где
, где  называются фокусами эллипса.
называются фокусами эллипса. .
. .
. на этой линии до его фокусов
на этой линии до его фокусов  и
и  постоянна.
постоянна.
 (70)
(70) и
и  , точка
, точка  - центр эллипса,
- центр эллипса, 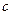 - половина расстояния между фокусами эллипса.
- половина расстояния между фокусами эллипса. , фокусы эллипса сливаются,
, фокусы эллипса сливаются,  и мы имеем окружность радиуса
и мы имеем окружность радиуса 




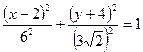
 и
и  и центром в точке
и центром в точке  .
.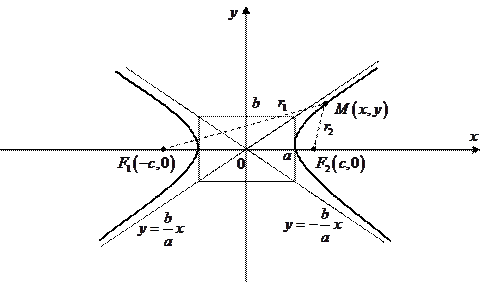

 (71)
(71) .
. являются наклонными асимптотами гиперболы. Эта линия имеет две оси симметрии, точка пересечения которых является центром симметрии гиперболы.
являются наклонными асимптотами гиперболы. Эта линия имеет две оси симметрии, точка пересечения которых является центром симметрии гиперболы. , а ее эксцентриситет
, а ее эксцентриситет  принимает любые значения, больше единицы. Вершины гиперболы имеют координаты
принимает любые значения, больше единицы. Вершины гиперболы имеют координаты  и
и 

 лежит на параболе, если
лежит на параболе, если 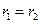 . Отсюда выводится каноническое уравнение параболы, которое имеет вид:
. Отсюда выводится каноническое уравнение параболы, которое имеет вид: (72)
(72) называется фокусом параболы, а прямая
называется фокусом параболы, а прямая  - ее директрисой.
- ее директрисой.


