
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диагональная форма матрицы оператораСодержание книги
Поиск на нашем сайте Наиболее простой вид матрица
Следовательно, для того чтобы привести матрицу Пример. Привести к диагональному виду матрицу Решение. Характеристическое уравнение этой матрицы имеет вид:
Найдем собственные векторы, подставляя найденные собственные значения в матричное уравнение
отсюда
Откуда Поскольку собственные значения этой матрицы
Проверим это по формуле
Найдем определитель матрицы
По формуле
4.6. Квадратичные формы.
4.6.1. Основные сведения о квадратичных формах. Определение. Квадратичной формой
Предполагаем, что коэффициенты квадратичной формы Будем называть симметрическую матрицу
матрицей квадратичной формы (50). Квадратичная форма (50) может быть представлена в матричной форме:
где В самом деле
Пример. Дана квадратичная форма Решение. Матрица этой квадратичной формы имеет следующий вид: на главной диагонали стоят коэффициенты при квадратах переменных, а симметричные относительно нее недиагональные элементы равны половинам соответствующих коэффициентов перекрестных произведений переменных данной квадратичной формы. Следовательно:
4.6.2. Преобразование квадратичных форм. Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных. Пусть векторы-столбцы переменных
где
Итак, при невырожденном линейном преобразовании
Пример. Для квадратичной формы предыдущего примера найти квадратичную форму, полученную из данной линейным преобразованием Решение. Матрица данного линейного преобразования имеет вид:
Применяя формулу (53) к матрице
т.е. квадратичная форма принимает вид:
4.6.3. Канонический и нормальный виды квадратичной формы. Определение. Квадратичная форма
т.е. матрица является диагональной.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Определение. Квадратичная форма с действительными коэффициентами имеет нормальный вид, если в ее каноническом виде все коэффициенты равны 1 или -1.
Существуют различные методы приведения квадратичной формы к каноническому виду. Рассмотрим один из них Метод Лагранжа. Заключается в выделении полных квадратов: сначала формируется полный квадрат из слагаемых, содержащих
Пример. Привести к каноническому и нормальному виду квадратичную форму
Решение. Применяя метод Лагранжа, получаем:
где
Теорема. (Закон инерции квадратичных форм). При любом способе приведения квадратичной формы (50) с действительными коэффициентами к нормальному виду число квадратов с коэффициентами 1 получается одно и то же, как и число квадратов с коэффициентами -1.
4.6.4. Критерий знакоопределенности квадратичной формы. Определение. Квадратичная форма (50) называется положительно определенной (отрицательно определенной), если для любых значений переменных Оба этих случая объединены под названием знакоопределенных форм. Если квадратичная форма (50) как положительные, так и отрицательные значения, то она называется знакопеременной. Квадратичная форма Аналогично в нормальный вид отрицательно определенной все Миноры
называются главными минорами матрицы
Теорема. (критерий Сильвестра). Для того чтобы квадратичная форма (50) была положительно определенной, необходимо и достаточно, чтобы были выполнены условия
Для того, чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров
Пример. Найти по критерию Сильвестра знакоопределенность квадратичной формы
Решение. Матрица этой квадратичной формы имеет вид:
Последовательно вычисляем ее миноры
Поскольку критерий Сильвестра не соблюден, то данная квадратичная форма является знакопеременной.
Линейная модель торговли Одним из примеров экономического процесса, приводящего к понятию собственного числа и собственного вектора матрицы, является процесс взаимных закупок товаров. Будем полагать, что бюджеты Пусть
Тогда, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), то справедливо условие
Матрица (57) со свойством (58), в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для
Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е.
Если считать, что
Покажем, что в условиях (59) не может быть знака неравенства. Действительно, сложим все неравенства системы (60). Группируя слагаемые с величинами бюджетов
Учитывая (58), выражения в скобках равны единице, следовательно, мы приходим к противоречивому неравенству
откуда очевиден только знак равенства. Таким образом, неравенства (60) принимают знак равенства
С экономической точке зрения это понятно, так как все страны не могут одновременно получать прибыль. Введя вектор бюджетов
Уравнение (62) означает, что собственный вектор структурной матрицы Перепишем уравнение (62) в виде, позволяющим определять
Пример. Структурная матрица торговли четырех стран имеет вид
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:
Решение. Находим собственный вектор
Найдем ранг этой системы, для этого преобразуем матрицу к ступенчатому виду:
Поскольку ранг этой системы равен трем, то имеем три основных переменных
Из последнего уравнения системы находим
Из первого уравнения системы, учитывая найденные значения
Итак, Подставив найденные значения в заданную сумму бюджетов, найдем величину
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

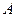 линейного оператора
линейного оператора 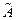 имеет, когда базисом является система ее собственных векторов, т.е. все
имеет, когда базисом является система ее собственных векторов, т.е. все  ее собственных
ее собственных  значений различны. В этом случае
значений различны. В этом случае 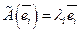 ,
,  при
при  и
и  , т.е. матрица
, т.е. матрица  .
.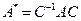 , в качестве матрицы
, в качестве матрицы  нужно взять матрицу, столбцами которой должны быть собственные векторы оператора
нужно взять матрицу, столбцами которой должны быть собственные векторы оператора  .
.
 , откуда
, откуда  ,
, 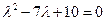 ,
,  .
. получаем
получаем ,
,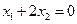 . Полагая
. Полагая  произвольной константой, получаем собственный вектор
произвольной константой, получаем собственный вектор  . Подстановка второго собственного значения
. Подстановка второго собственного значения  приводит к уравнению
приводит к уравнению ,
, , полагая
, полагая 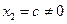 получаем второй собственный вектор матрицы
получаем второй собственный вектор матрицы  . Поскольку
. Поскольку  и
и 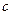 - произвольные числа, одному собственному значению может соответствовать несколько собственных векторов разной длины.
- произвольные числа, одному собственному значению может соответствовать несколько собственных векторов разной длины.
 .
. , а обратная матрица
, а обратная матрица 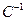 имеет вид:
имеет вид:
 .
. от
от  (50)
(50) - действительные числа, причем
- действительные числа, причем  .
. (51)
(51) (52)
(52) и
и 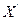 - вектор-строка и вектор-столбец переменных.
- вектор-строка и вектор-столбец переменных.
 .
. . Записать ее в матричном виде.
. Записать ее в матричном виде.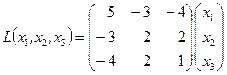
 и
и  связаны линейным соотношением
связаны линейным соотношением
 ,
,  есть некоторая невырожденная матрица
есть некоторая невырожденная матрица  .
. (53)
(53) ,
, 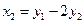 ,
, 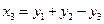 .
. .
. ,
, .
.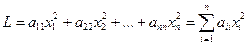 (54)
(54) , затем из слагаемых, содержащих
, затем из слагаемых, содержащих  и т.д. Рассмотрим это на конкретном примере.
и т.д. Рассмотрим это на конкретном примере.




 .
. ,
,  ,
,  . При приведении к нормальному виду в этой квадратичной форме нужно использовать замену переменных
. При приведении к нормальному виду в этой квадратичной форме нужно использовать замену переменных  ,
, 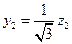 ,
,  . Тогда получаем:
. Тогда получаем: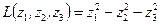
 , не равных одновременно нулю, указанная форма имеет положительные (отрицательные) значения.
, не равных одновременно нулю, указанная форма имеет положительные (отрицательные) значения.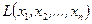 от
от 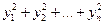 . Понятно, что все
. Понятно, что все  ,
,  ,
,  ,…,
,…, 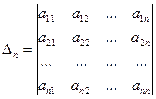 (55)
(55) (56)
(56) чередовались, причем
чередовались, причем  .
. .
.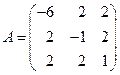 .
. ,
,  ,
,  .
.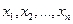 , расходуются на покупку товаров. Будем рассматривать линейную модель обмена, или, как ее еще называют, модель международной торговли.
, расходуются на покупку товаров. Будем рассматривать линейную модель обмена, или, как ее еще называют, модель международной торговли. , которую
, которую  -ая страна тратит на закупку товаров у
-ая страна тратит на закупку товаров у  -ой страны. Введем матрицу коэффициентов
-ой страны. Введем матрицу коэффициентов  (57)
(57) (58)
(58) .
. или
или ,
,  (59)
(59) , то получаем систему неравенств
, то получаем систему неравенств (60)
(60)
 ,
, (61)
(61) (каждая компонента этого вектора характеризует бюджет соответствующей страны). Тогда систему уравнений (61) можно записать в матричной форме
(каждая компонента этого вектора характеризует бюджет соответствующей страны). Тогда систему уравнений (61) можно записать в матричной форме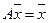 , (62)
, (62) , состоит из бюджетов стран бездефицитной международной торговли.
, состоит из бюджетов стран бездефицитной международной торговли. и решать соответствующие задачи
и решать соответствующие задачи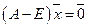
 .
. (усл. ден. ед.)
(усл. ден. ед.) , которое в нашем случае имеет вид
, которое в нашем случае имеет вид



 и одну свободную -
и одну свободную -  . Выразим основные переменные
. Выразим основные переменные 
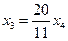 , далее найденное значение
, далее найденное значение  подставляет во второе уравнение системы:
подставляет во второе уравнение системы: ,
,  ,
,  ,
, 
 и
и  :
: ,
, ,
,  ,
, 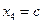 , тогда
, тогда  ,
,  ,
,  .
.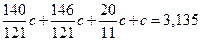


 , откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах):
, откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах): ,
,  ,
,  ,
,  .
.


