
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определителей и применение их для решения системы линейных алгебраических уравнений.Содержание книги
Поиск на нашем сайте
БИЛЕТ №1. Свойства определителей и применение их для решения системы линейных алгебраических уравнений. Определители n-ного порядка. Определитель существует только для квадратной матрицы. Определитель матрицы – разность произведения элементов. Определитель матрицы = Детерминант матрицы Определитель квадратной матрицы – число, которое вычисляется по следующему правилу:
Пример:
Определитель второго порядка.
Определитель третьего порядка. Правило треугольника или Сюрриса.
Минор. Минором Алгебраическое дополнение Алгебраическим дополнением Теорема о понижении порядка определителя Теорема утверждает, что любой определитель равен сумме по парных произведений всех элементов какой либо строки (столбца) на алгебраические дополнения. Свойства определителей. 1. При транспонировании матрицы её определитель не меняется. 2. При перестановке двух строк определителя, он меняет свой знак, но по абсолютной величине не меняется. 3. При умножении определителя на число, достаточно умножить любую строку на это число. 4. Если определитель содержит нулевую строку, то он равен нулю. 5. Свойство упрощения определителя. Определитель не изменяется, если к элементам любой его строки прибавить элементы любой другой его строки, предварительно умножив их на одно и тоже любое число. 6. Сумма определителей, отличающихся одной строкой, равна определителю с теми же элементами, у которого вместо различных строк стоит строка из суммы элементов различных строк. 7. Если определитель имеет две пропорциональные строки, то он равен нулю. 8. Сумма попарных произведений элементов кокой либо строки и алгебраических дополнений соответствующих элементов другой строки равна нулю. 9. Определитель произведения двух квадратных матриц равен произведению их определителей. 10.Определитель треугольной матрицы равен произведению своих диагональных элементов. БИЛЕТ №2. Решение системы линейных алгебраических уравнений методом Жордана Гаусса.
Алгоритм: 1. В каждом уравнении выделить по одной базисной переменной (со знаком) 2. Выразить базисные переменные через остальные (свободные). 3. Выписать общее решение.
Базисная переменная – переменная, которая присутствует только в одном уравнении.
Метод Ж.Гаусса = Метод последовательного исключения
Обычно имеется общее и частное решение.
Если в каждом уравнении нет по базисной переменной, то следует сделать элементарные преобразования.
«КОНКУРС КРАСОТЫ» 1) КОНКУРС МЕЖДУ СТОЛБЦАМИ Складываем столбцами и выбираем меньшую переменную (без знаков) 2) КОНКУРС МЕЖДУ СТРОЧКАМИ Складываем строчками и выбираем меньшую переменную (без знаков)
Метод последовательного исключения неизвестных заключается в решении системы алгебраических уравнений с одновременным исследованием её на совместность. Метод реализуется в два этапа: Прямой ход метода. Прямой ход метода Гаусса заключается в преобразовании расширенной матрицы коэффициентов системы к ступенчатому виду с помощью элементарных преобразований, то есть как при нахождении ранга матрицы и базисного минора, но только со строками матрицы. При этом само преобразование к ступенчатому виду с помощью нескольких шагов, на каждом из которых исключается одна переменная, то есть обнуляется нижний элемент одного из столбцов. В результате выполнения нескольких шагов матрица оказывается приведённой к ступенчатому виду. На этом этапе можно определить ранг матрицы и системы. Если ранг расширенной матрицы равен рангу матрицы коэффициентов, то система считается совместной, в противном случае система не совместна. Если количество уравнений равно количеству неизвестных, то система имеет единственное решение, если ранг системы меньше числа неизвестных, то количество решений бесконечно. Обратный ход метода. Если решение единственно: БИЛЕТ №3. Операции над матрицами. 1. Сложение [1] – суммой двух матриц А и В одного порядка называют матрицу С того же порядка, каждый элемент которой равен сумме соответствующих элементов двух первых матриц. Матрицы разных порядков сложению не подлежат. 2. Умножение матрицы на число: Произведение матрицы и числа – есть матрица того же порядка, каждый элемент которой умножен на число. 3. Произведение матриц согласованных[2] порядков:
4. Транспонирование – это операция, при которой элементы строк матрицы А становятся элементами столбцов матрицы В. Свойства умножения матриц. 1. 2. АВС=А(ВС)≠(АС)В 3. А(В+С)=АВ+АС а) С(А+В)=СА+СВ б) (С+В)А=ВА+СА 4. 5. 6. (АВ)Т=ВТАТ 7. (АТ)Т=А Замечание:
БИЛЕТ №4. Свойства умножения матриц. 1. 2. АВС=А(ВС)≠(АС)В 3. А(В+С)=АВ+АС а) С(А+В)=СА+СВ б) (С+В)А=ВА+СА 4. 5. 6. (АВ)Т=ВТАТ 7. (АТ)Т=А Замечание:
БИЛЕТ №5. Теорема о ранге. Ранг матрицы соответствует количеству её линейно независимых строк, или столбцов. Рангом матрицы называется порядок её базисного минора. (Базисным минором матрицы А называется такой минор порядка r, который не равен нулю, а все миноры рангом выше равны, или не существуют.)
БИЛЕТ №6. БИЛЕТ №7. БИЛЕТ №8. Векторная алгебра. Ø Геометрическим вектором называется направленный отрезок прямой, который можно переносить параллельно самому себе. Ø Модулем вектора называется его длина. Ø Нулевым вектором называется вектор, начало и конец которого совпадают. Ø Коллинеарными называются вектора, лежащие на параллельных прямых. Ø Равными называются коллинеарные, со направленные вектора, имеющие одинаковую длину. Ø Компланорными называются векторы, расположенные в одной и той же, или в параллельных плоскостях. Теорема №1. Два колиниарных вектора всегда линейно зависимы. Теорема №2. Три комплонарных[5] вектора всегда линейно зависимы. Теорема №3. Любые четыре геометрических вектора линейно зависимы.
Базис. Базисом на плоскости, или в пространстве называется максимальная система из линейно независимых векторов. 1) Базис на прямой является единственным вектором, параллельным данной прямой. 2) Базис на плоскости – это любая пара из не коллинеарных векторов, параллельных этой плоскости. 3) Базис в пространстве – это любые три не комплонарных вектора. Разложение вектора по базису называется представление его в виде линейной комбинации векторов базиса. Теорема. Для заданного вектора а и выбранного базиса разложение, по базису является единственным. БИЛЕТ №9. БИЛЕТ №10. Проекция вектора на вектор.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Свойства. 1) 2) 3) 4) 5)
Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей. БИЛЕТ №11. БИЛЕТ №12. БИЛЕТ №13. БИЛЕТ №14. БИЛЕТ №15. Общее уравнение прямой. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
БИЛЕТ №16. БИЛЕТ №17. БИЛЕТ №18. БИЛЕТ №19. БИЛЕТ №20. БИЛЕТ №21. БИЛЕТ №22. Пример. Найдите расстояние между параллельными прямыми Решение. Очевидно, что прямая, которой соответствуют параметрические уравнения прямой на плоскости вида Искомое расстояние между параллельными прямыми равно расстоянию от точки Получим нормальное уравнение прямой, которой отвечает уравнение прямой с угловым коэффициентом вида Второй способ решения. Получим общие уравнения заданных параллельных прямых. Выше мы выяснили, что прямой Коэффициенты при переменных x и y в полученных общих уравнениях параллельных прямых равны, поэтому мы сразу можем применить формулу для вычисления расстояния между параллельными прямыми на плоскости: Ответ:
БИЛЕТ №23. БИЛЕТ №24. Условия перпендикулярности. Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам. А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве? Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.
Теорема. Для перпендикулярности прямых a и b необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен направляющему вектору прямой b.
Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых. Добавим конкретики. Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданы уравнения прямой на плоскости некоторого вида, определяющие прямые a и b. Обозначим направляющие векторы прямых а и b как Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.
БИЛЕТ №25. БИЛЕТ №26. БИЛЕТ №27. БИЛЕТ №28. БИЛЕТ №29. БИЛЕТ №30. БИЛЕТ №31. БИЛЕТ №32. БИЛЕТ №33. БИЛЕТ №34. БИЛЕТ №35. БИЛЕТ №36. БИЛЕТ №37. БИЛЕТ №38. Пример. Найдите координаты точки пересечения прямой Решение. Подставим в уравнение плоскости выражения Находим координаты точки пересечения прямой и плоскости по параметрическим уравнениям при Ответ: (3, 0, -1).
Пример. Если прямая Решение. Составим систему из заданных уравнений Последнее уравнение системы после прямого хода метода Гаусса стало неверным равенством, следовательно, система уравнений не имеет решений. Отсюда заключаем, что прямая Ответ: прямая параллельна плоскости и они не имеют точки пересечения.
БИЛЕТ №39. БИЛЕТ №40. БИЛЕТ №41. БИЛЕТ №42. БИЛЕТ №43. БИЛЕТ №44. БИЛЕТ №45. БИЛЕТ №46. Уравнение окружности.
Уравнение окружности ω (A; R) имеет вид (x – a)2 + (y – b)2 = R2, где a и b – координаты центра A окружности ω (A; R).
БИЛЕТ №47. Уравнение эллипса.
Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух заданных фокусов есть величина постоянная.
a,b – полуоси эллипса.
БИЛЕТ №48. Уравнение гиперболы.
Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний каждой из которых до двух заданных фокусов, находящихся на расстоянии 2с является величиной постоянной, равной 2а.
Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы.
БИЛЕТ №49. Уравнение параболы.
Параболой называется геометрическое место точек плоскости, каждая из которых равноудалена от заданной точки – фокуса, и заданной прямой, называемой директрисой, причём расстояние от точки до прямой равно р.
y ² = 2 px БИЛЕТ №50. БИЛЕТ №1. Свойства определителей и применение их для решения системы линейных алгебраических уравнений.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.143.18 (0.011 с.) |

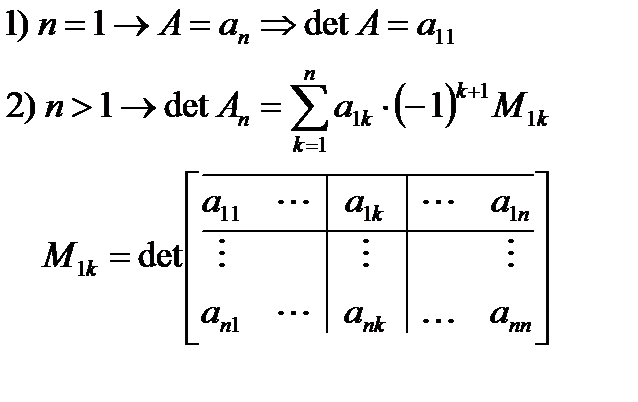
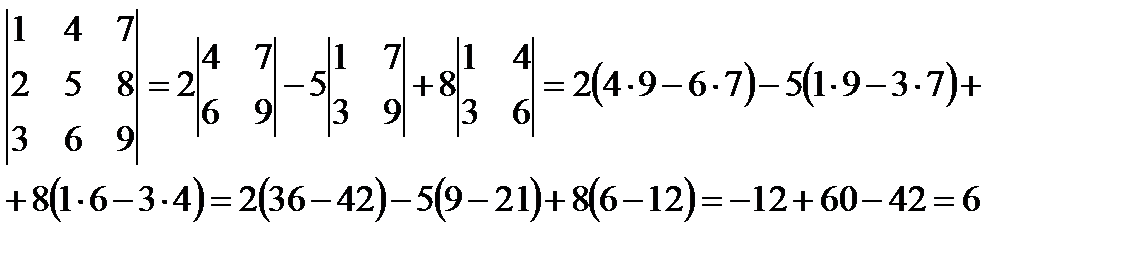
 (X перемножаем)
(X перемножаем) квадратной матрицы п -ного порядка называется определитель п- 1 -ого порядка, полученный из определителя матрицы А вычёркиванием i-той строки и j-того столбца.
квадратной матрицы п -ного порядка называется определитель п- 1 -ого порядка, полученный из определителя матрицы А вычёркиванием i-той строки и j-того столбца. называется минор этого элемента, взятый с определённым знаком, который определяется по формуле:
называется минор этого элемента, взятый с определённым знаком, который определяется по формуле: 






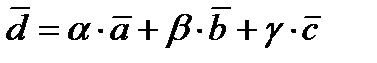


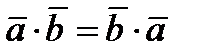 – Коммутативность.
– Коммутативность.




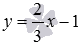 и
и  .
.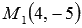 .
. . Теперь вычислим нормирующий множитель:
. Теперь вычислим нормирующий множитель:  . Умножив на него обе части последнего уравнения, имеем нормальное уравнение прямой:
. Умножив на него обе части последнего уравнения, имеем нормальное уравнение прямой:  . Искомое расстояние равно модулю значения выражения
. Искомое расстояние равно модулю значения выражения  , вычисленного при
, вычисленного при  . Итак, расстояние между заданными параллельными прямыми равно
. Итак, расстояние между заданными параллельными прямыми равно
 . Перейдем от параметрических уравнений прямой вида
. Перейдем от параметрических уравнений прямой вида 
 .
. .
. и
и  соответственно. По уравнениям прямых a и b можно определить координаты направляющих векторов этих прямых – получаем
соответственно. По уравнениям прямых a и b можно определить координаты направляющих векторов этих прямых – получаем  и
и  . Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов
. Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов  .
.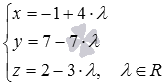 и плоскости
и плоскости  .
. :
:
 :
:
 пересекается с плоскостью
пересекается с плоскостью  , то найдите координаты точки их пересечения.
, то найдите координаты точки их пересечения. . Для нахождения ее решения используем метод Гаусса. Метод Гаусса позволит нам не только определить, имеет ли записанная система уравнений одно решение, бесконечное множество решений или не имеет ни одного решения, но и найти решения в случае их наличия.
. Для нахождения ее решения используем метод Гаусса. Метод Гаусса позволит нам не только определить, имеет ли записанная система уравнений одно решение, бесконечное множество решений или не имеет ни одного решения, но и найти решения в случае их наличия.







