
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение расстояния между параллельными прямыми на плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Расстояние между двумя параллельными прямыми – это расстояние от произвольной точки одной из параллельных прямых до другой прямой.
Для наглядности изобразим две параллельные прямые a и b, отметим на прямой а произвольную точку М1, опустим перпендикуляр из точки М1 на прямую b, обозначив его H1. Отрезок М1H1 соответствует расстоянию между параллельными прямыми a и b.
Приведенное определение расстояния между двумя параллельными прямыми справедливо как для параллельных прямых на плоскости, так и для прямых в трехмерном пространстве. Более того, такое определение расстояния между двумя параллельными прямыми принято не случайно. Оно тесно связано со следующей теоремой.
Теорема. Все точки одной из двух параллельных прямых удалены на одинаковое расстояние от другой прямой. Доказательство. Рассмотрим параллельные прямые a и b. Отметим на прямой a точку М1, опустим из нее перпендикуляр на прямую b. Основание этого перпендикуляра обозначим как H1. Тогда длина перпендикуляра М1H1 есть расстояние между параллельными прямыми a и b по определению. Докажем, что
Так как внутренние накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны (об этом говорилось в статье параллельные прямые, параллельность прямых), то Следует заметить, что расстояние между двумя параллельными прямыми является наименьшим из расстояний от точек одной прямой до точек другой прямой.
Нахождение расстояния между параллельными прямыми – теория, примеры, решения. Итак, нахождение расстояния между параллельными прямыми сводится к нахождению длины перпендикуляра, проведенного из некоторой точки одной из прямых на другую прямую. При этом подбирается метод, позволяющий это расстояние отыскать. Выбор метода зависит от условий конкретной задачи. В некоторых случаях можно использовать теорему Пифагора, в других - признаки равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п. Если же параллельные прямые заданы в прямоугольной системе координат, то расстояние между заданными параллельными прямыми можно вычислить методом координат. На нем и остановимся. Сформулируем условие задачи. Пусть на плоскости или в трехмерном пространстве зафиксирована прямоугольная система координат, заданы две параллельные прямые a и b и требуется найти расстояние между этими прямыми. Решение этой задачи строится на определении расстояния между параллельными прямыми - чтобы найти расстояние между двумя заданными параллельными прямыми нужно: определить координаты некоторой точки М1, лежащей на прямой a (или на прямой b); вычислить расстояние от точки М1 до прямой b (или a). С определением координат точки М1, лежащей на какой-нибудь из заданных параллельных прямых, проблем не возникнет, если, конечно, Вам знакомы основные виды уравнения прямой на плоскости и уравнения прямой в пространстве. Для нахождения расстояния от точки М1 до нужной из заданных параллельных прямых Вам будет полезна информация из раздела нахождение расстояния от точки до прямой. В частности, если в прямоугольной системе координат Oxy на плоскости прямую a задает общее уравнение прямой вида Покажем вывод этой формулы. Возьмем точку Если То есть, при любом значении С2 расстояние Разберем решения примеров. Начнем с нахождения расстояния между двумя параллельными прямыми, заданными в прямоугольной системе координат Oxy на плоскости.
Пример. Найдите расстояние между параллельными прямыми Решение. Очевидно, что прямая, которой соответствуют параметрические уравнения прямой на плоскости вида Искомое расстояние между параллельными прямыми равно расстоянию от точки Получим нормальное уравнение прямой, которой отвечает уравнение прямой с угловым коэффициентом вида Второй способ решения. Получим общие уравнения заданных параллельных прямых. Выше мы выяснили, что прямой Коэффициенты при переменных x и y в полученных общих уравнениях параллельных прямых равны, поэтому мы сразу можем применить формулу для вычисления расстояния между параллельными прямыми на плоскости: Ответ:
БИЛЕТ №23.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |


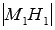 равно
равно  , где М2 – произвольная точка прямой a, отличная от точки M1, а H2 – основание перпендикуляра, проведенного из точки М2 на прямую b. Доказав этот факт, мы докажем и саму теорему.
, где М2 – произвольная точка прямой a, отличная от точки M1, а H2 – основание перпендикуляра, проведенного из точки М2 на прямую b. Доказав этот факт, мы докажем и саму теорему.
 , а прямая M2H2, перпендикулярная прямой b по построению, перпендикулярна и прямой a. Тогда треугольники М1H1H2 и М2М1H2 прямоугольные, и, более того, они равны по гипотенузе и острому углу: М1H2 – общая гипотенуза,
, а прямая M2H2, перпендикулярная прямой b по построению, перпендикулярна и прямой a. Тогда треугольники М1H1H2 и М2М1H2 прямоугольные, и, более того, они равны по гипотенузе и острому углу: М1H2 – общая гипотенуза, 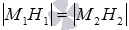 . Теорема доказана.
. Теорема доказана. , а прямую b, параллельную прямой a, - общее уравнение прямой
, а прямую b, параллельную прямой a, - общее уравнение прямой  , то расстояние
, то расстояние  .
. , которая лежит на прямой a, тогда координаты точки М1 удовлетворяют уравнению
, которая лежит на прямой a, тогда координаты точки М1 удовлетворяют уравнению  , откуда имеем
, откуда имеем  .
. , то нормальное уравнение прямой b имеет вид
, то нормальное уравнение прямой b имеет вид 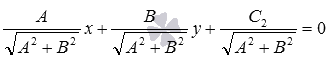 , а если
, а если  , то нормальное уравнение прямой b имеет вид
, то нормальное уравнение прямой b имеет вид  . Тогда при
. Тогда при 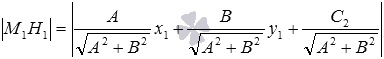 , а при
, а при 
 . На этом вывод формулы для вычисления расстояние между двумя параллельными прямыми, заданными общими уравнениями прямых вида
. На этом вывод формулы для вычисления расстояние между двумя параллельными прямыми, заданными общими уравнениями прямых вида 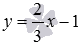 и
и  .
.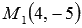 .
. . Теперь вычислим нормирующий множитель:
. Теперь вычислим нормирующий множитель:  . Умножив на него обе части последнего уравнения, имеем нормальное уравнение прямой:
. Умножив на него обе части последнего уравнения, имеем нормальное уравнение прямой:  . Искомое расстояние равно модулю значения выражения
. Искомое расстояние равно модулю значения выражения  , вычисленного при
, вычисленного при  . Итак, расстояние между заданными параллельными прямыми равно
. Итак, расстояние между заданными параллельными прямыми равно
 . Перейдем от параметрических уравнений прямой вида
. Перейдем от параметрических уравнений прямой вида 
 .
. .
.


