Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние от точки до прямой в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если s={m;n;p}-направляющий вектор прямой l, M1(x1, y1, z1) - точка лежащей на прямой, тогда расстояние от точки M0(x0, y0, z0) до прямой l можно найти, используя формулу
Вывод формулы Если задано уравнение прямой l то несложно найти s= {m; n; p} - направляющий вектор прямой и M1(x1, y1, z1) - координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах S = |M0M1×s|.
S = |s|d.
d, а сторона параллелограмма равна модулю направляющего вектора s. 26) Прямая в пространстве Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений. Итак, если уравнения двух непараллельных плоскостей --
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему. Уравнения (11.11) называют общими уравнениями прямой в пространстве. 27) Общее уравнение плоскости в декартовой системе координат записывается следующим образом:
Если известно, что плоскость проходит через точку с координатами (x 0, y 0, z 0), то ее уравнение можно привести к виду
Уравнение
называется уравнением плоскости в отрезках на осях. Нормаль к плоскости имеет координаты Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a 1 x + b 1 y + c 1 z + d 1 = 0 и a 2 x + b 2 y + c 2 z + d 2 = 0, то угол между плоскостями равняется
Расстояние от точки (x 0; y 0; z 0) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно
28) Угол между плоскостями Пусть плоскости Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку
Рис.11.6.Угол между плоскостями
Если через точку
Рис.11.7.Угол между нормальными векторами острый
Рис.11.8.Угол между нормальными векторами тупой
В одном варианте (рис. 11.7) Во втором варианте (рис. 11.8)
то в обоих случаях По определению скалярного произведения
и соответственно
Так как координаты нормальных векторов известны, если заданы уравнения плоскостей, то полученная формула (11.4) позволяет найти косинус острого угла между плоскостями. Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Получаем условие перпендикулярности плоскостей:
Если плоскости параллельны, то коллинеарны их нормальные векторы. Получаем условие параллельности плоскостей
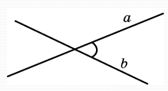
где 29) Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
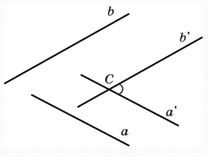
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
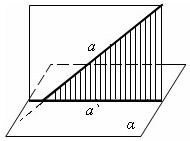
30) Угол между прямой и плоскостью Прямая a пересекает плоскость α. а не перпендикулярна плоскости. Основания перпендикуляров, опущенных из точек прямой a на плоскость α, лежат на прямой a`. Эта прямая называется проекцией прямой a на плоскость α. Угол между прямой и проекцией этой прямой на плоскость называется углом между прямой и плоскостью.
31)
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.233 (0.008 с.) |

 Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую. и
и  , то прямая, являющаяся их линией пересечения, задается системой уравнений
, то прямая, являющаяся их линией пересечения, задается системой уравнений
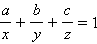



 и
и 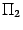 заданы соответственно уравнениями
заданы соответственно уравнениями  между этими плоскостями.
между этими плоскостями. на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры
на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры  и
и  к линии пересечения. Нарисуем также нормальные векторы
к линии пересечения. Нарисуем также нормальные векторы  и
и  плоскостей
плоскостей 
 , перпендикулярную линии пересечения плоскостей
, перпендикулярную линии пересечения плоскостей 

 и
и  , следовательно, угол
, следовательно, угол  между нормальными векторами равен углу
между нормальными векторами равен углу  , а угол
, а угол 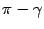 . Так как
. Так как
 .
. . Откуда
. Откуда

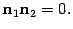

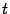 -- любое число.
-- любое число.