
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование неявных и параметрически заданных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Неявно заданная функция Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция). Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у. Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот. Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0). Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'. Производная неявной функции выражается через аргумент х и функцию у. << Пример 21.1 Найти производную функции у, заданную уравнением х3+у3-3ху=0. Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения 3х2+3у2· у'-3(1· у+х· у')=0 следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х). Функция, заданная параметрически Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
где t — вспомогательная переменная, называемая параметром. Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции
Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х. << Пример 21.2 Пусть Найти у'х. Решение: Имеем x't=3t2, y't=2t. Следовательно, у'х=2t/t2, т. е. В этом можно убедиться, найдя непосредственно зависимость у от х. Действительно, 60) Понятие дифференциала Пусть функция y = f (x) дифференцируема при некотором значении переменной x. Следовательно, в точке x существует конечная производная
Тогда по определению предела функции разность
является бесконечно малой величиной при
(величина Если
оно является бесконечно малой того же порядка малости, что и
Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно
Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают
или
Следовательно,
или
Итак, дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной. Замечание. Нужно помнить, что если x – исходное значение аргумента,
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (5) это видно из записи, в формуле (4) – нет. Дифференциал функции можно записать в другой форме:
или
Геометрический смысл дифференциала. Дифференциал функции y = f (x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении x на величину 61) Инвариантность формы дифференциала первого порядка. Следствие 2.4.1. dz = F′(y0)dy = Φ′(x0)dx. В зтой формуле dy = f′(x)dx является дифференциалом функции, а dx дифференциалом независимой переменной. – 75 –Таким образом, дифференциал функции z имеет один и тот же вид (а именно, произведение производной функции на дифференциал переменной) независимо от того, считается ли эта переменная независимой (dz = Φ′(x0)dx) или она является функцией (dz = F′(y0)dy). В этом и заключается инвариантность формы дифференциала (первого порядка). Замечание 2.4.2. Если приходится иметь дело со сложной функцией z =z(y), y = y(x), то для обозначения ее производной употребляется также индекс x или y, указывающий, по какой переменной берется производная, т.е. пишут z′x или z′y. В этих обозначениях формула для вычисления производной сложной функции имеет вид z′x = z′yy′x. 62)
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 4041; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.123.61 (0.006 с.) |






 Тогда
Тогда  Отсюда
Отсюда  т. е.
т. е. 

 (1)
(1) . Выразив из равенства (1) приращение функции, получим
. Выразив из равенства (1) приращение функции, получим (2)
(2)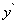 не зависит от
не зависит от  , т. е. остаётся постоянной при
, т. е. остаётся постоянной при  , то в правой части равенства (2) первое слагаемое
, то в правой части равенства (2) первое слагаемое  линейно относительно
линейно относительно  - бесконечно малая более высокого порядка малости, чем первое, так как их отношение
- бесконечно малая более высокого порядка малости, чем первое, так как их отношение  стремится к нулю при
стремится к нулю при
 (3)
(3)
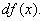
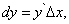 (4)
(4)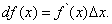 (5)
(5)
 (6)
(6)
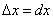 .
.


