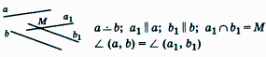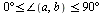Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекция вектора на направление другого вектораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для проекции вектора
В координатной форме формула для проекции примет вид
21)
Результатом векторного произведения векторов является ВЕКТОР: Определение: Векторным произведением Векторное произведение коллинеарных векторов Определение подробно разобрано, осталось выяснить, что происходит, когда векторы Таким образом, если Частный случай – векторное произведение вектора на самого себя: Смешанное произведение векторов – это произведение трёх векторов: Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят. Сначала опять определение и картинка: Определение: Смешанным произведением Выполним рисунок. Невидимые нам линии прочерчены пунктиром: Смешанное произведение компланарных векторов Если векторы Немного отвлекусь от темы, возможно, не все знают ответы на следующие вопросы:
С позиции геометрии ответ таков: нулю Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора Примечание: чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма. Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах
22) Выражение векторного произведения
которую можно записать с помощью определителя
Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам
23) Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. 24)
25)
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.011 с.) |

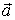 на направление вектора
на направление вектора  из определения скалярного произведения имеем
из определения скалярного произведения имеем .
. .
. , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву
, то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву 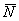 .
. неколлинеарных векторов
неколлинеарных векторов  , взятых в данном порядке, называется ВЕКТОР
, взятых в данном порядке, называется ВЕКТОР  имеет правую ориентацию:
имеет правую ориентацию:
 – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
– синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая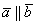 , то
, то  . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
. Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.

 , взятых в данном порядке, называется объём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис
, взятых в данном порядке, называется объём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис  правый, и знаком «–», если базис
правый, и знаком «–», если базис 
 .
.

 (а, значит, и малинового вектора
(а, значит, и малинового вектора 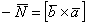 ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах
) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах 

 через проекции векторов
через проекции векторов  и
и  на координатные оси прямоугольной системы координат дается формулой
на координатные оси прямоугольной системы координат дается формулой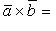



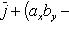
 (27)
(27)

 (28)
(28)
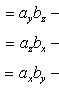
 (29)
(29)