
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции нескольких переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функция
где В этой записи функция
является дифференциалом функции
где Каждая дифференцируемая в точке функция имеет в этой точке все частные производные, но не каждая функция, имеющая все частные производные, является дифференцируемой. Более того, существование частных производных в некоторой точке не гарантирует даже непрерывность функции в этой точке. В качестве такого примера можно рассмотреть функцию двух переменных 54) Связь между дифференцируемостью и непрерывностью функции Рассмотрим следующие вопросы, который касаются функций. Если функция непрерывна, то она дифференцируема? Если функция дифференцируема, то она непрерывна? Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость. Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность. Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт. Найдем производную следующей функции
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
данный предел равен 1, если 55) Правила дифференцирования Ключевые слова: дифференцируемая функция, свойство предела произведения, дифференцируема в точке Если функции f и g дифференцируемы в точке x 0 то в этой же точке дифференцируемы сумма, произведение и частное (если g 1. (f + g) 2. (f 3. (fg) Постоянный множитель C можно выносить из-под знака производной: (Cf) ' = Cf '. В частности, С'=0
56) Производная обратной функции Дифференцируемая монотонная функция f: ] a, b [ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f -1, производная которой вычисляется по формуле
57)
58)
59)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.127 (0.008 с.) |

 переменных
переменных 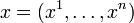 является дифференцируемой в точке
является дифференцируемой в точке 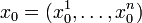 своей области определения
своей области определения  , если для любой точки
, если для любой точки  существуют такие константы
существуют такие константы  , что
, что
 .
.
 в точке
в точке  , а числа
, а числа  являются частными производными функции
являются частными производными функции 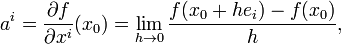
 — вектор, все компоненты которого, кроме
— вектор, все компоненты которого, кроме  -ой, равны нулю, а
-ой, равны нулю, а 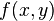 , равную
, равную 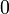 при
при 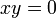 и
и  при
при  . В начале координат обе частные производные существуют (равны нулю), но функция не является непрерывной.
. В начале координат обе частные производные существуют (равны нулю), но функция не является непрерывной. . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:
. Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

 и равен (-1), если
и равен (-1), если  , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
, получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема. (x 0)
(x 0) 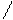 =0) этих функций, причем
=0) этих функций, причем g)
g) 
 g − f
g − f  N также дифференцируема, причем (fn)
N также дифференцируема, причем (fn) 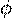 (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем
(y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем 

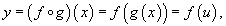 где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция  также дифференцируема по x и ее производная
равна
также дифференцируема по x и ее производная
равна
 Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на
производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная
внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в
друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на
производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная
внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в
друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".
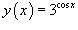 .
Решение.
Поскольку
.
Решение.
Поскольку  , то по правилу производной сложной функции получаем
, то по правилу производной сложной функции получаем

 =n
=n  xn−1
xn−1
 x
x
 x
x
 a
a 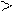 0
0  =1
=1
 lna
lna



