
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные признаки возрастания и убывания функции.Содержание книги
Поиск на нашем сайте
Вот формулировки признаков:
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
67) 7) Наибольшим значением функции y = f(x) на промежутке X называют такое значение, что для любого справедливо неравенство. Наименьшим значением функции y = f(x) на промежутке X называют такое значение, что для любого справедливо неравенство. Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе. Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль. 68) Выпуклость функции и точки перегиба Непрерывная на отрезке [ a; b ] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x 1 и x 2 из этого отрезка
Другими словами, если для любых точек x 1 и x 2 отрезка [ a; b ] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх. Аналогично определяется функция, выпуклая вниз. Дважды дифференцируемая на [ a; b ] функция f (x) выпукла вверх, если для любого
Дважды дифференцируемая на [ a; b ] функция f (x) выпукла вниз, если для любого
Так, вторая производная функции Пусть функция f (x) непрерывна в точке Необходимое условие наличия точки перегиба. Если
Достаточные условия наличия точки перегиба. Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке Если
В заключение приведем примеры, когда точка x 0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
Не являются точками перегиба и точки возврата, например точка 69) Тема № 8. Асимптоты Определение 1. Асимптотой графика функции называется прямая, к которой неограниченно приближается график функции при Различают вертикальные и наклонные асимптоты (в частности, горизонтальные). Прямая х = а называется вертикальной асимптотой, если хотя бы один из односторонних пределов Пример 24. Найти вертикальные асимптоты функции
Решение. Знаменатель дроби равен нулю в точках х = – 1, х = +1. Значит функция в этих точках не определена. Классифицируем разрыв, вычислив односторонние пределы. Эту работу можно уменьшить, если учесть чётность функции:
Следовательно, прямые х = – 1, х = 1 – вертикальные асимптоты. Прямая у = b называется горизонтальной асимптотой, если выполняется условие В частности, это полупрямая у = b при Так в примере 23 функция Определение 2. Прямая у = k х + b называется наклонной асимптотой графика функции f (х) при f (х) = kх + b + a (х), где То есть разность a (х) между ординатами точек кривой и асимптоты при Теорема. Чтобы график функции имел наклонную асимптоту, необходимо и достаточно, чтобы имели место соотношения:
причём при Если k = 0,
у = b, то есть получаем уравнение горизонтальной асимптоты. Пример 25. Найти асимптоты графиков функций: 25.1. Решение
Значит, функция в точке х = 3 терпит бесконечный разрыв и через эту точку проходит вертикальная асимптота х = 3. Найдём наклонную асимптоту, используя соотношения (21)
Получили горизонтальную асимптоту у = 1. Строим график функции, подсчитав ориентировочную точку (6,2) (см рис. 26). 25.2. Функция Вычисляем односторонние пределы:
Значит, х = 2 – уравнение вертикальной асимптоты. Ищем уравнение наклонной асимптоты в виде у = k х + b:
Уравнение асимптоты Проверка. Согласно определению, функцию можно представить в виде
70)
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.008 с.) |

 и
и  на области определения;
на области определения;




 равна
равна  откуда следует, что квадратичная функция выпукла вниз на всей области определения.
откуда следует, что квадратичная функция выпукла вниз на всей области определения. и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 
 Если
Если  меняет знак при переходе через точку
меняет знак при переходе через точку  то
то 
 то
то 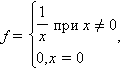
 );
);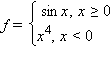

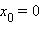 у функции
у функции 
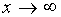 или
или  .
.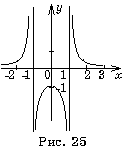
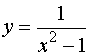 .
. ,
, .
.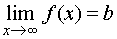 .
. .
. (см. рис. 25).
(см. рис. 25). , если эту функцию можно представить в виде:
, если эту функцию можно представить в виде: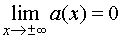 .
. ,
,  , (21)
, (21) , уравнение асимптоты принимает вид
, уравнение асимптоты принимает вид ; 25.2.
; 25.2.  .
. 25.1. Функция не определена в точке х = 3 (знаменатель дроби равен нулю). Классифицируем разрыв с помощью односторонних пределов:
25.1. Функция не определена в точке х = 3 (знаменатель дроби равен нулю). Классифицируем разрыв с помощью односторонних пределов: ,
,  .
. ,
,  .
. ;
; 
 ;
;
 (см. рис. 27).
(см. рис. 27).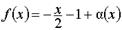 . Проверим это, выделив целую часть дроби. Разделим числитель на знаменатель:
. Проверим это, выделив целую часть дроби. Разделим числитель на знаменатель:
 ,
, 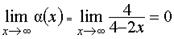 .
.


