
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лассификация точек разрыва функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. 51) 4. Свойства функций, непрерывных на отрезке. Функцию f(x) называют непрерывной на отрезке [ а, b ], если она непрерывна в каждой точке интервала (а, Ь) и, кроме того, непрерывна справа в точке а и непрерывна слева в точке b. а) Ограниченность непрерывной на отрезке функции. Теорема 3 (Вейерштрасса). Если функция f непрерывна на отрезке [а, b], то она ограничена, т. е. - Предположим противное, тогда Полагая в (4) С = 1, 2,..., n,..., получим, что Последовательность
где в силу условия (5) для любого
Из условий (6) и (7) следует, что
С другой стороны, утверждение (5) выполняется при всех
откуда следует, что Это противоречит равенству (8), согласно которому последовательность { б) Достижимость точных граней. Теорема 4 (Вейерштрасса). Если функция f непрерывна на отрезке [а,b], то она достигает своей точной верхней и нижней грани, т. е.
○ Так как непрерывная на отрезке функция f (x) ограничена (теорема 3), т. е. множество значений, принимаемых функцией f на отрезке [а, b], ограничено, то существуют
Докажем утверждение (9). Обозначим М =
Полагая
f( Из соотношений (11), (13) и (14) следует, что
откуда получаем
Как и в теореме 3, из условия (13) следует, что существуют подпоследовательность {
В силу непрерывности функции f в точке
С другой стороны, { Поэтому
В силу единственности предела последовательности из (16) и (17) заключаем, что f ( Аналогично доказывается утверждение (10). ●
в) Промежуточные значения. Теорема 5 (теорема Коши о нулях непрерывной функции). Если функция f непрерывна на отрезке [а, b] и принимает в его концах значения разных знаков, т. е. f(a)f(b) < 0, то на отрезке [а,b] имеется хотя бы один нуль функции f, т. е. О Разделим отрезок [а, b] пополам. Пусть d — середина этого отрезка. Если f(d) = 0, то теорема доказана, а если 1. 2. Продолжая эти рассуждения, получим: 1)либо через конечное число шагов найдется точка 2)либо существует последовательность отрезков и По теор. Кантора существует точка с, принадлежащая всем отрезкам последовательности,
Докажем, что f(с) = 0. (21) Предположим, что равенство (21) не выполняется. Тогда либо f(с) > 0, либо f(с) < 0. Пусть, например, f(с) > 0. По свойству сохранения непрерывной функцией знака
С другой стороны, из неравенства (19) следует, что
Так как с
что в концах каждого из отрезков Полученное противоречие доказывает, что должно выполняться условие (21). • 52) ПРОИЗВОДНАЯ ФУНКЦИИ
Геометрический: Если функция
Функция Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки –известная функция x (t) времени t. В течение интервала времени от t 0 до t 0 +
отсюда, v (t 0) = x’ (t 0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t). 53) Функции одной переменной Функция
при этом число
Функция одной переменной является дифференцируемой в точке График функции
доставляет касательную прямую к этой кривой, проведённую в точке Напр., функция
При этом её производная есть Элементарные функции могут быть непрерывны в некоторой точке, но не быть в ней дифференцируемы. Напр., функция Графики элементарных функций учат, что произвольная функция дифференцируема всюду, за исключением исключительных и изолированных значений аргумента. Первая попытка аналитического доказательства этого утверждения принадлежит Амперу, и поэтому оно носит название гипотезы Ампера. Это утверждение, однако, не верно в классе аналитически представимых функций, напр., функция Дирихле не является даже непрерывной ни в одной точке. Нельзя также считать и произвольную непрерывную функцию дифференцируемой, напр.,функция Вейерштрасса определена и непрерывная на всей вещественной оси, но не является дифференцируемой ни в одной её точке[6]. Это в частности означает, что к её графику ни в одной точке нельзя провести касательную прямую. Тем не менее, гипотезу Ампера можно рассматривать как нестрогую формулировку следующей теоремы Лебега: любая монотонная функция
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.161 (0.012 с.) |

 и правосторонний предел
и правосторонний предел  ;
;

 называется скачком функции.
называется скачком функции. (3)
(3) (4)
(4) (5)
(5) ограничена, так как
ограничена, так как  для всех
для всех 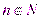 . По теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность, т. е. существуют подпоследовательность
. По теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность, т. е. существуют подпоследовательность  и точка
и точка  такие, что
такие, что , (6)
, (6) выполняется неравенство
выполняется неравенство . (7)
. (7) [а, b], а из условия (6) в силу непрерывности функции f в точке
[а, b], а из условия (6) в силу непрерывности функции f в точке  получаем
получаем . (8)
. (8) и, в частности, при n =
и, в частности, при n =  (k =1,2,...), т. е.
(k =1,2,...), т. е. ,
, , так как
, так как 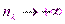 при
при  .
. } имеет конечный предел. Поэтому условие (4) не может выполняться, т. е. справедливо утверждение (3).●
} имеет конечный предел. Поэтому условие (4) не может выполняться, т. е. справедливо утверждение (3).● =
=  (9)
(9) =
=  . (10)
. (10) и
и  .
. (11)
(11) (12)
(12) = 1,
= 1,  ,
,  ,...,
,...,  ,..., получим в силу условия (12) последовательность
,..., получим в силу условия (12) последовательность  , где
, где  , такую, что для всех
, такую, что для всех  выполняются условия
выполняются условия (13)
(13) )>M -
)>M - 
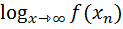 . (15)
. (15) } последовательности {
} последовательности {  такие, что
такие, что , где
, где  [а, Ь].
[а, Ь].
 . (16)
. (16) )} — подпоследовательность последовательности {
)} — подпоследовательность последовательности {  }, сходящейся, согласно условию (15), к числу М.
}, сходящейся, согласно условию (15), к числу М. . (17)
. (17) ) = М =
) = М =  (18)
(18) , то в концах одного из отрезков [a, d], [d,b] функция fпринимает значения разных знаков. Обозначим этот отрезок
, то в концах одного из отрезков [a, d], [d,b] функция fпринимает значения разных знаков. Обозначим этот отрезок 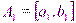 . Пусть
. Пусть  — середина отрезка
— середина отрезка  Возможны два случая:
Возможны два случая: , тогда теорема доказана;
, тогда теорема доказана; , тогда в концах одного из отрезков
, тогда в концах одного из отрезков  ,
,  функция f принимает значения разных знаков; такой отрезок обозначим
функция f принимает значения разных знаков; такой отрезок обозначим  .
. такая, что f(с) = 0; тогда справедливо утверждение (18);
такая, что f(с) = 0; тогда справедливо утверждение (18); такая, что
такая, что  для всех
для всех  , где An = [an,bn]; эта последовательность отрезков является стягивающейся, так как
, где An = [an,bn]; эта последовательность отрезков является стягивающейся, так как  для любого
для любого 
 (19)
(19) т. е.
т. е.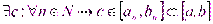 . (20)
. (20)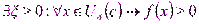 . (22)
. (22) при
при  , и поэтому
, и поэтому . (23)
. (23) в силу условия (20), то из (23) следует, что
в силу условия (20), то из (23) следует, что  и согласно условию (22) во всех точках отрезка
и согласно условию (22) во всех точках отрезка  функция f принимает положительные значения. Это противоречит тому,
функция f принимает положительные значения. Это противоречит тому, функция f принимает значения разных знаков.
функция f принимает значения разных знаков.
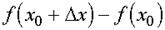
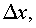


 имеет конечную производную в точке
имеет конечную производную в точке  то в окрестности
то в окрестности  её можно приблизить линейной функцией
её можно приблизить линейной функцией
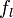 называется касательной к
называется касательной к  в точке
в точке  Число
Число  является угловым коэффициентом или тангенсом угла наклона касательной прямой.
является угловым коэффициентом или тангенсом угла наклона касательной прямой. точка перемещается на расстояние: x (t 0 +
точка перемещается на расстояние: x (t 0 +  , а её средняя скорость равна: va =
, а её средняя скорость равна: va =  0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:
 одной переменной является дифференцируемой в точке
одной переменной является дифференцируемой в точке  своей области определения
своей области определения  , если существует такая константа
, если существует такая константа  , что для любой точки
, что для любой точки  верно
верно

 представляет собой кривую на плоскости
представляет собой кривую на плоскости  , а график линейной функции
, а график линейной функции
 определена и дифференцируема в любой вещественной точке, поскольку её можно представить в виде
определена и дифференцируема в любой вещественной точке, поскольку её можно представить в виде .
. , а уравнение касательной прямой, проведённой в точке
, а уравнение касательной прямой, проведённой в точке  .
. является непрерывной на всей вещественной оси, но её производная испытывает скачок при переходе через точку
является непрерывной на всей вещественной оси, но её производная испытывает скачок при переходе через точку  , в котором эта функция не является дифференцируемой. В этой точке нельзя провести и касательную к графику функции. Функция
, в котором эта функция не является дифференцируемой. В этой точке нельзя провести и касательную к графику функции. Функция  тоже непрерывна на всей вещественной оси и её график имеет касательные во всех точках, однако касательная, проведённая в точке
тоже непрерывна на всей вещественной оси и её график имеет касательные во всех точках, однако касательная, проведённая в точке  имеет определённую конечную производную всюду, кроме, быть может, некоторого множества значений
имеет определённую конечную производную всюду, кроме, быть может, некоторого множества значений  меры нуль.
меры нуль.


