
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки разрыва и их классификация.Содержание книги Поиск на нашем сайте
Как было сказано выше, функция f(x) непрерывна в точке х0, если
Если в точке х0 это двойное равенство не выполняется, то точка х0 называется точка разрыва функции. Точками разрыва будем называть также точки, в которых f(x) не определена, но в любой d-окрестности которых имеются точки области определения функции f(x). Классификация точек разрыва. Пусть 1) (можно доопределить функцию в точке х0: f(x0)=f(x0+0)=f(x0-0))/
2) Существуют конечные пределы А+-А- - скачок функции в точке х0. Эта функция определена всюду, кроме точки х0=0, но в любой d-окрестности этой точки имеются точки области определения этой функции. Следовательно, х0=0 – точка разрыва функции f(x)=
Т.о. существуют конечные односторонние пределы, но они не равны. Значит, х0=0 – точка разрыва 1-го рода. Величина скачка функции в этой точке: f(+0)-f(-0)= 3) Если в точке х0 не существует хотя бы один из односторонних пределов или в точке х0 хотя бы один из односторонних пределов бесконечен, то х0 – точка разрыва 2-го рода. Например, функция
Пример. Исследовать на непрерывность функцию f(x)= Функции у=х3+1, у=2 и у=3х непрерывны на всей числовой прямой, поэтому данная функция может иметь разрыв только в точках, где меняется ее аналитическое выражение, т.е. в точках х1=1 и х2=2. Исследуем функцию на непрерывность в этих точках, для чего соответствующие найдем односторонние пределы и значения функции. 1) В точке х1=1.
Т.о. 2) В точке х2=2
Т.о. Скачок функции в точке х2: 6-2=4. График. f(x)= В точке х1=-Π разрыв 1-го рода и непрерывна слева. Скачок функции в точке х1 равен -Π. В точке х2=Π/2 – точка устранимого разрыва (f(Π/2) – неопределенно). Свойства функций, непрерывных в замкнутом промежутке. Первая теорема Больцано-Коши. (Теорема об обращении функции в ноль) Теорема 1. Пустьфункция f(x) определена и непрерывна на отрезке [a,b] и на концах этого отрезка принимает значения разных знаков (т.е. f(a)∙f(b)<0), то внутри отрезка найдется такая точка с Замечание. Эта теорема есть достаточное условие для разрешимости уранвений вида f(x)=0. На ней основывается метод интервалов. Доказательство.
2) f(c1)≠0, т.е. либо f(с1)>0, либо f(с1)<0. Тогда на концах только одного из отрезков [a,с1] и [с1,b] функция принимает значения разных знаков. Обозначим этот отрезок I1=[a1,b1]. Разделим отрезок I1 пополам точкой с2= 2) f(c2)≠0, т.е. либо f(с2)>0, либо f(с2)<0. Тогда на концах только одного из отрезков [a1,с2] и [с2,b1] функция принимает значения разных знаков. И т.д. до бесконечности. Если на некотором шаге мы получим точку ck такую, что f(ck)=0, то теорема доказана. В противном случае мы получим последовательность вложенных отрезков: I1ÉI2É…ÉIkÉ… На k-м шаге получим отрезок Ik=[ak,bk] такой, что f(ak)>0 f(bk)>0 Согласно лемме о вложенных отрезках
Последовательность левых концов аk→c, k→¥ Последовательность правых концов bk→c, k→¥ Т.к. 0£с-аk£êIkê= По условию, функция f(x) непрерывна на отрезке [a,b], а значит непрерывна и в точке сÎ[a,b]. Следовательно, f(c)= Но f(ak)>0 и Получили, что f(c)³0 и f(c)£0, следовательно, f(c)=0. ч.т.д. Замечание. Требование непрерывности функция f(x) во всех точках отрезка [a,b] существенно. Например, рассмотрим функцию f(x)=
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |


 =f(x0+0)=А+ и
=f(x0+0)=А+ и  =f(x0-0)=А – правый и левый односторонний пределы.
=f(x0-0)=А – правый и левый односторонний пределы. А+=А-≠f(x0) - х0 – точка устранимого разрыва.
А+=А-≠f(x0) - х0 – точка устранимого разрыва. Пример. f(x)=
Пример. f(x)= 
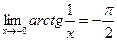 ,
, 
 =p.
=p.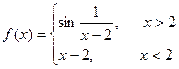 - определена всюду, кроме точки х0=2, но в любой d-окрестности этой точки имеются точки области определения этой функции. Следовательно, х0=2 – точка разрыва функции f(x). Т.к. функция не имеет предела при х→2, то это точка разрыва 2-го рода.
- определена всюду, кроме точки х0=2, но в любой d-окрестности этой точки имеются точки области определения этой функции. Следовательно, х0=2 – точка разрыва функции f(x). Т.к. функция не имеет предела при х→2, то это точка разрыва 2-го рода. 2) Функция у=
2) Функция у=  - в точке х=3 имеет точку разрыва 2-го рода, т.к. односторонние пределы бесконечны.
- в точке х=3 имеет точку разрыва 2-го рода, т.к. односторонние пределы бесконечны. ,
, 


 значение f(1) - неопределенно
значение f(1) - неопределенно , т.е. точка х1=1 – точка устранимого разрыва функции.
, т.е. точка х1=1 – точка устранимого разрыва функции.
 f(2)=2
f(2)=2 f(2)=2, т.е. точка х2 – точка разрыва 2-го рода.
f(2)=2, т.е. точка х2 – точка разрыва 2-го рода.
 (a,b) такая, что f(с)=0.
(a,b) такая, что f(с)=0.  (Рисунок)
(Рисунок) 1) Пусть для определенности f(a)>0, f(b)<0. Разделим отрезок [a,b] пополам, получим точку с1=
1) Пусть для определенности f(a)>0, f(b)<0. Разделим отрезок [a,b] пополам, получим точку с1= 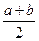 . Тогда возможны 2 варианта: 1) f(c1)=0 – тогда точка с1-искомая
. Тогда возможны 2 варианта: 1) f(c1)=0 – тогда точка с1-искомая . Тогда возможны 2 варианта: 1) f(c2)=0 – тогда точка с1-искомая
. Тогда возможны 2 варианта: 1) f(c2)=0 – тогда точка с1-искомая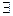 сÎIk, k=1,2,…
сÎIk, k=1,2,… Покажем, что f(с)=0.
Покажем, что f(с)=0. и 0→0,k→¥ и
и 0→0,k→¥ и  =
= 
 на отрезке [-1,1]. Хотя на концах этого отрезка функция и принимает значения разных знаков, но в нуль на [-1,1] не обращается, т.к. не является непрерывной в точке х=0.
на отрезке [-1,1]. Хотя на концах этого отрезка функция и принимает значения разных знаков, но в нуль на [-1,1] не обращается, т.к. не является непрерывной в точке х=0.


