
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вторая теорема Больцано-Коши (о промежуточных значениях непрерывной функции).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пустьфункция f(x) определена и непрерывна на отрезке [a,b] и f(a)≠f(b), тогда для любого числа С, заключенного между числами f(a) и f(b) найдется такая точка ξ
Доказательство. Пусть, для определенности, f(a)<f(b), тогда f(a)<c<f(b). Введем вспомогательную функцию φ(х)=f(x)-c Тогда φ(а)=f(a)-c<0, φ(b)=f(b)-c>0. Следовательно, по теореме 1, между точками a и b обязательно найдется хотя бы одна точка ξ такая, что φ(ξ)=f(ξ)-c=0, т.е. f(ξ)=c. Ч.т.д. Первая теорема Вейерштрасса (об ограниченности функции). Пусть функция f(x) определена и непрерывна на отрезке [a,b], тогда она ограничена на этом отрезке, т.е. существуют числа m и М такие, что m£f(x)£М Доказательство. Допустим противное, что функция f(x) не является ограниченной на отрезке [a,b]. Тогда найдется хотя бы одно х1Î[a,b] такое, что êf(x1)ê>1. Аналогично, можно указать х2Î[a,b] такое, что êf(x2)ê>2. И т.д. продолжая этот процесс, получим последовательность х1,х2,…,xn,… Такой, что С другой стороны, полученная последовательность ограничена, т.к. А из ограниченной последовательности можно извлечь сходящуюся подпоследовательность. Пусть это будет подпоследовательность Тогда Переходя в этом неравенстве к пределу при k→¥, получаем a£x0£b, т.е. х0Î[a,b]. По условию функция f(x) непрерывна на отрезке [a,b]. Значит f(x) непрерывна и в точке х0. Т.к. С другой стороны, последовательность êf( Сопоставляя (2) и (3) получаем противоречие. Следовательно ч.т.д. Замечание. Требование непрерывности функции f(x) на отрезке [a,b] существенно. Если функция f(x) непрерывна на интервале (a,b) или полуинтервале [a,b) ((a,b]), то нельзя гарантировать ограниченность f(x) на этих промежутках. Например, рассмотрим функцию f(x)= Вторая теорема Вейерштрасса (о минимальном и максимальном значении. Пусть функция f(x) определена и непрерывна на отрезке [a,b], тогда она существуют такие точки из отрезка [a,b], в которых функция принимает наименьшее значение m и наибольшее значение М. (Рисунок) Доказательство. По теореме об ограниченности непрерывной функции, множество значений, которые принимает функция f(x) на отрезке [a,b] ограниченно. Следовательно, существуют его точная верхняя и точная нижняя границы. Пусть М= Покажем, что f(x) достигает в промежутке [a,b] наибольшее значение. Для этого надо доказать, что в промежутке [a,b] имеется хотя бы одна точка х0 такая, что f(x0)=М. Допустим, что такой точки в промежутке [a,b] нет. Тогда Введем вспомогательную функцию Функция φ(х) определена и непрерывна на отрезке [a,b] как отношение двух непрерывных функций с необращающимся в 0 знаменателем. Более того, φ(х)>0 на [a,b]. Следовательно, к φ(х) можно применить первую теорему Вейерштрасса, т.е. φ(х)£К или Т.к. неравенство (*) выполняется Получили противоречие. Следовательно, на промежутке [a,b] обязательно имеется хотя бы одна точка х0, в которой функция f(x) принимает свое наибольшее значение. Аналогично доказывается, что функция f(x) принимает в промежутке [a,b] свое наименьшее значение. Ч.т.д. Три важных предела. 1. Покажем, что
2. Покажем, что Положим ах-1=уÞах=1+уÞх Имеем
Следовательно, 3. Покажем, что Положим (1+х)a-1=уÞ(1+х)a=1+уÞa Имеем
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.45 (0.008 с.) |

 (a,b) такая, что f(ξ)=С. (Рисунок)
(a,b) такая, что f(ξ)=С. (Рисунок)

 хÎ[a,b].
хÎ[a,b]. и пусть
и пусть 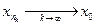 .
.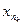 £b.
£b. является подпоследовательностью для последовательности
является подпоследовательностью для последовательности  . Учитывая (1) получаем, что должно быть
. Учитывая (1) получаем, что должно быть на промежутке (0,1]. В каждой конкретной точке этого промежутка она принимает конечное значение, но f(x)=
на промежутке (0,1]. В каждой конкретной точке этого промежутка она принимает конечное значение, но f(x)=  , m=
, m= 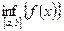 (M и m – конечные числа).
(M и m – конечные числа). справедливо неравенство: М-f(x)>0 (т.к. М=
справедливо неравенство: М-f(x)>0 (т.к. М= 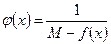 .
.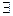 K>0:
K>0:  Þf(x)£M-
Þf(x)£M- 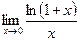 =1.
=1.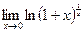 . Т.к. логарифмическая функция непрерывна, то
. Т.к. логарифмическая функция непрерывна, то
 =
=  .
. , При х→0, у→0.
, При х→0, у→0. =
=  =
=  =
=  Перейдем в этом равенстве к пределу:
Перейдем в этом равенстве к пределу: По доказанному ранее,
По доказанному ранее,  .
. =a.
=a. =ln(1+y), При х→0, у→0.
=ln(1+y), При х→0, у→0.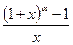 =
=  =
= 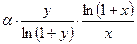 Перейдем в этом равенстве к пределу:
Перейдем в этом равенстве к пределу: По доказанному ранее,
По доказанному ранее, 


