
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства непрерывных функций.Содержание книги Поиск на нашем сайте Арифметические операции над непрерывными функциями. Теорема 1. Пусть функции f(x) и g(x) определены в одном и том же промежутке X и непрерывны в точке х0, то в этой же точке будут непрерывны и функции f(x)±g(x), f(x)×g(x), Доказательство. Вытекает из теорем о пределе алгебраической суммы, произведения и частного двух функций, имеющих пределы. Докажем, в качестве примера, непрерывность Т.к. функции f(x) и g(x) непрерывны в точке х0, то По теореме о пределе частного (т.к. предел знаменателя не нуль), имеем:
Теорема 2. Непрерывность сложной функции. Пусть даны функции f и φ: Доказательство 1. Возьмем e>0. Т.к. функция f(u) непрерывна в точке u0ÎU, то можно указать такое число σ>0, что для всех uÎU таких, что |u-u0|<σ выполняется неравенство |f(u)- f(u0)|<e.
Т.к. φ(х) непрерывна в точке х0ÎХ, то можно указать такое число δ>0, что для всех хÎХ таких, что |x-x0|<δ выполняется неравенство |φ(х)- φ(x0)|<e.
Из полученных соотношений следует, что если |x-x0|<δ, то функция F=f(φ(x)) определена и выполняется неравенство |f(φ(х))-f(φ(x0))|<e. А это и означает непрерывность функции F=f(φ(x)) в точке х0. Ч.т.д. Доказательство 2. Возьмем произвольную последовательность {xn} такую, что xn→x0, n→¥. Тогда, в силу непрерывности функции φ(х) в точке х0, будет: φ(хn)→φ(x0), при n→¥. Т.е. un→u0, n→¥ (т.к. xnÎX, то un=φ(хn)ÎU при всех n). Т.к. un→u0, n→¥, то в силу непрерывности f(u) в точке u0, имеем: f(un)→f(u0), n→¥, т.е. f(φ(xn))→f(φ(x0)), n→¥, а это и означает непрерывность функции F=f(φ(x)) в точке х0. Ч.т.д. Из теоремы 2 следует: т.е под знаком непрерывной функции можно переходить к пределу. Пример. Примеры непрерывных функций. 1) f(x)ºС, хÎ(-¥;+¥) – непрерывна в любой точке х0Î(-¥;+¥). Действительно, пусть точка х0 – любая из (-¥;+¥). Возьмем произвольную последовательность {xn} такую, что xn→x0, n→¥. Соответствующая последовательность значений функции будет такой: f(x1)=С, f(x2)=С, …, f(xn)=С, …. f(xn)→С=f(x0), при n→¥. А это означает, что функция f(x) непрерывна в точке х0. Т.к. точка х0 – любая точка из промежутка (-¥;+¥). Следовательно, f(x) непрерывна в промежутке (-¥;+¥). Или DС=С-С=0. 2) f(x)=x, xÎ(-¥;+¥) Выберем произвольную точку х0Î(-¥;+¥). Возьмем произвольную последовательность {xn} такую, что xn→x0, n→¥. Соответствующая последовательность значений функции будет такой: f(x1)=x1, f(x2)=x2, …, f(xn)=xn, …. f(xn)→x0=f(x0), при n→¥. А это означает, что функция f(x) непрерывна в точке х0. Т.к. точка х0 – любая точка из промежутка (-¥;+¥). Следовательно, f(x)=х непрерывна в промежутке (-¥;+¥). 3) f(x)=xn, xÎ(-¥;+¥), nÎN Эта функция непрерывна в промежутке (-¥;+¥), т.к. f(x)=х∙х∙…∙х. Следовательно, f(x)=xn непрерывна в промежутке (-¥;+¥) как произведение конечного числа функций, непрерывных в этом промежутке. 4) f(x)=a0xn+a1xn-1+a2xn-2+…+an-1x+an, xÎ(-¥;+¥), nÎN – целая рациональная функция, полином – непрерывна в промежутке (-¥;+¥) как сумма конечного числа функций, непрерывных в этом промежутке. 5) 6) Покажем, что функция f(x)=sin x непрерывна на всей своей области определения, т.е. на R=(-¥;+¥). Возьмем х0. Рассмотрим |sin x - sin x0|=2 (т.к. |sin x| <|x-x0|)Т.о. |sin x - sin x0|£|x-x0| Возьмем δ=e, тогда 7) Аналогично доказывается непрерывность функции f(x)=cos x. 8) 9) Аналогично Все основные элементарные функции непрерывны на своей области определения. Теорема 3. Пусть функция f(x) непрерывна в точке х0ÎХ. Тогда существует окрестность V(x0) точки х0, на которой функция ограничена. Т.е.
Доказательство. Т.к. f(x) непрерывна в точке х0, то
Возьмем e=1 и оценим êf(x)ê=êf(x)-f(x0)+f(x0)ê£êf(x)-f(x0)ê+ êf(x0)ê<1+êf(x0)ê Т.о. êf(x)ê<1+êf(x0)ê, т.е. f(x) – ограничена. Ч.т.д. Теорема 4. Пусть функция f(x) непрерывна в точке х0ÎХ и f(x0)≠0. Тогда существует окрестность V(x0) точки х0, на которой
Причем, если f(x0)>0, если f(x0)<0,
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.005 с.) |

 (последняя при условии, что g(x0)≠0).
(последняя при условии, что g(x0)≠0). и
и 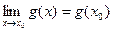
 , а это и означает, что функция
, а это и означает, что функция  . Если функция φ(х) непрерывна в точке х0ÎХ, а функция f(u) непрерывна в точке u0ÎU, то функция F=f(φ(x)) будет непрерывна в точке х0.
. Если функция φ(х) непрерывна в точке х0ÎХ, а функция f(u) непрерывна в точке u0ÎU, то функция F=f(φ(x)) будет непрерывна в точке х0. e>0
e>0 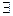 σ=σ(e)
σ=σ(e)  |f(σ)- f(σ0)|<e
|f(σ)- f(σ0)|<e

 , nÎN, mÎN - дробная рациональная функция- непрерывна в любой такой точке х0Î(-¥;+¥), в которой знаменатель отличен от нуля, т.е. f(x) непрерывная в каждой точке своей области определения.
, nÎN, mÎN - дробная рациональная функция- непрерывна в любой такой точке х0Î(-¥;+¥), в которой знаменатель отличен от нуля, т.е. f(x) непрерывная в каждой точке своей области определения. x: |x-x0|<δ
x: |x-x0|<δ  £2
£2 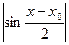 £2
£2  =|x-x0|
=|x-x0|

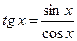 ,
, 
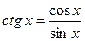 ,
, 
 и
и 


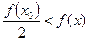 (xÎV(x0))
(xÎV(x0))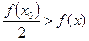 (xÎV(x0))
(xÎV(x0))


