
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики непрерывной случайной величиныСодержание книги
Поиск на нашем сайте
Напомним, что для дискретной случайной величины числовые характеристики определяются формулами:
Числовые же характеристики непрерывной случайной величины определяются формулами:
Эти характеристики имеют тот же смысл, что и в случае дискретной случайной величины. Пример 3. В условиях примера2 найти числовые характеристики непрерывной случайной величины Х. Решение
т. е. среднее значение случайной величины Х равно 1,5.
Или
Основные законы распределения Ранее мы ввели понятие «закон распределения случайной величины». В практических задачах наиболее часто встречаются следующие законы распределения: равномерный закон; биноминальный закон (Бернулли); закон Пуассона; геометрический закон; показательный закон; нормальный закон (закон Гаусса). Рассмотрим подробно каждый из них.
Равномерный закон распределения
Этот закон имеет место как для дискретной случайной величины, так и для непрерывной случайной величины. Дискретная случайная величина называется равномерно распределенной, если все её возможные значения имеют одинаковые вероятности, т. е. суммарная вероятность, равная единице, равномерно распределена между всеми возможными значениями случайной величины. Закон распределения такой случайной величины имеет вид:
В этом случае
Дискретная случайная величина Х, рассмотренная в примере о мишени п.2.2.3, имеет равномерный закон распределения:
Среднее значение Непрерывная случайная величина называется равномерно распределенной на отрезке [a, b], если её плотность вероятности задается формулой:
График плотности вероятности изображен на рис. 2.10.
Постоянная Найдем функцию распределения
График Теорема. Еслинепрерывная случайная величина равномерно распределена, то её числовые характеристики вычисляются по формулам:
Доказательство. По определению числовых характеристик непрерывной случайной величины и свойствам интеграла имеем:
1.
2.
3.
Примером равномерно распределенной непрерывной случайной величины могут быть: – время ожидания транспорта с постоянным интервалом движения; – ошибка измерения при округлении измеряемой величины до ближайшего целого деления.
Биномиальный закон распределения
Дискретная случайная величина Х имеет биномиальное распределение, если она может принимать значения 0, 1, 2, …, n с вероятностями
где
Например, случайная величина, равная количеству успехов в схеме Бернулли n повторных независимых испытаний, имеет биноминальное распределение. В этом случае m – число успехов, p – вероятность успеха, q – вероятность неуспеха. Ряд распределения этой случайной величины:
Теорема. Числовые характеристики дискретной случайной величины Х, распределенной по биномиальному закону, вычисляются по формулам:
Доказательство. Случайную величину Х – число успехов в n независимых испытаниях – можно представить в виде суммы n независимых случайных величин
где случайная величина
Найдем числовые характеристики случайной величины
Теперь найдем числовые характеристики рассматриваемой случайной величины Х:
что и требовалось доказать. Биномиальный закон распределения широко используется в теории и практике статистического контроля качества продукции, в теории массового обслуживания и других областях.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.007 с.) |

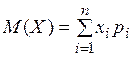 ,
,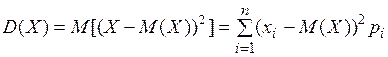 ,
,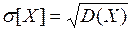 .
. ,
, ,
, ,
,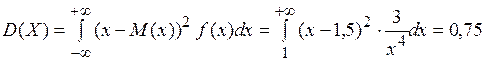 .
.
 .
.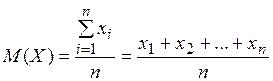 .
. .
. , что совпадает с ранее полученным результатом.
, что совпадает с ранее полученным результатом.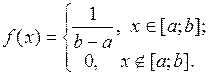
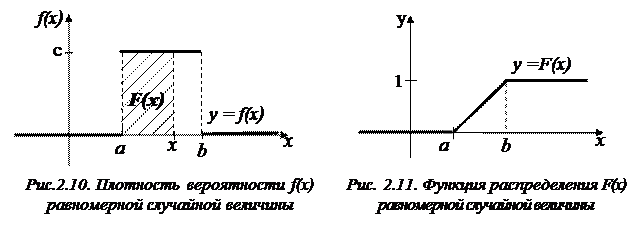
 , т. к. по свойству плотности вероятности площадь криволинейной трапеции, опирающейся на отрезок [a, b], должна быть равна единице.
, т. к. по свойству плотности вероятности площадь криволинейной трапеции, опирающейся на отрезок [a, b], должна быть равна единице.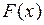 равномерно распределенной непрерывной случайной величины, используя её геометрический смысл (
равномерно распределенной непрерывной случайной величины, используя её геометрический смысл (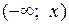 и ограниченной сверху кривой
и ограниченной сверху кривой 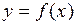 ):
):
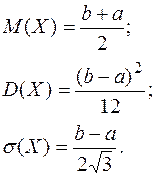 (2.5)
(2.5)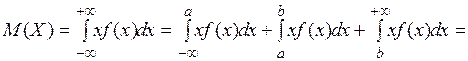
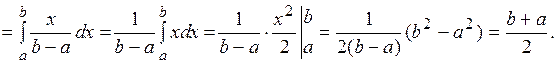
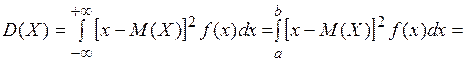
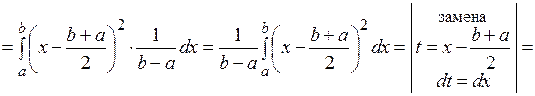
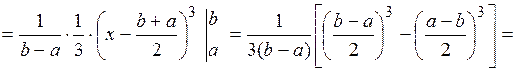
 .
. , теорема доказана.
, теорема доказана.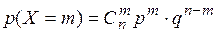 ,
,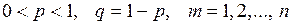 .
.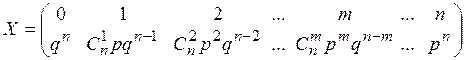 .
. (2.6)
(2.6)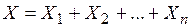 ,
,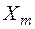 – число успехов в m-м испытании (m = 1, 2, …, n). Каждая из случайных величин
– число успехов в m-м испытании (m = 1, 2, …, n). Каждая из случайных величин 

 .
.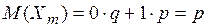 ,
,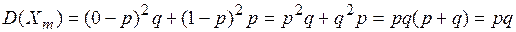 .
.
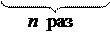


 ,
,


