
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ПРЕДИСЛОВИЕ
Это учебное пособие написано на основе лекций, прочитанных авторами в течение двух лет на экономическом факультете ОГИС. Изложенный материал соответствует требованиям Государственного образовательного стандарта по дисциплинам «Теория вероятностей и математическая статистика» для специальности 351400 – Прикладная информатика (в сфере сервиса) и дисциплине «Математика» для специальностей 060800 – Экономика и управление на предприятии сервиса и 060500 – Бухгалтерский учет, анализ и аудит. Пособие состоит из разделов «Элементы теории вероятностей», «Случайные величины», «Элементы математической статистики», Приложения. В конце каждого раздела читатель может найти упражнения для самопроверки. Ставя своей целью доступность излагаемого материала, авторы не всегда приводят строгие доказательства теоретических положений. Любопытный читатель сможет найти их в литературе, список которой прилагается. Известно, что учебный материал осваивается легче, если он сопровождается достаточно большим числом иллюстрирующих примеров, поэтому в пособии приведено много задач с решениями. Необходимые для решения задач таблицы математической статистики даются в приложениях. В конце пособия приводятся алфавитно-предметный указатель основных понятий курса и алфавитно-именной указатель ученых, внесших значительный вклад в развитие теории вероятностей и математической статистики. Изложение материала сопровождается такими средствами визуализации знаний, как рисунки, таблицы, схемы, что облегчит читателю восприятие материала. Благодаря большому числу разобранных задач экономического содержания, предлагаемое пособие может быть интересно не только студентам экономического факультета, но и специалистам, работающим в различных областях экономики, поскольку поможет им понять универсальность статистического анализа как инструмента решения проблем, связанных с риском и неопределенностью. Материал пособия является основой для последующего изучения студентами специальности 060800 дисциплины «Статистика». Авторы – доценты кафедры высшей математики и информатики ОГИС: кандидат физ.-мат. наук Н. В. Алексенко и кандидат педагогических наук Пособие рекомендовано заседанием кафедры высшей математики и информатики, протокол № 8 от 29.03. 2004 г. Утверждено научно-методическим советом специальности 351400, протокол № 5 от 30.03.2004 г.
Н. В Алексенко. ВВЕДЕНИЕ
Теория вероятностей изучает закономерности случайных явлений. Под случайным явлением понимают явление с неопределенным исходом, происходящее при неоднократном воспроизведении определенного комплекса условий. В природе, технике и экономике нет явлений, в которых не присутствовали бы элементы случайности. Существуют два подхода к изучению этих явлений. Первый – выделяются основные факторы, определяющие данное явление; влиянием второстепенных факторов, приводящих к случайным отклонениям, пренебрегают. Этот подход часто используется в «точных» науках. Второй – учитываются не только основные факторы, но и второстепенные (приводящие к случайным возмущениям и искажениям результата), вносящие элемент неопределенности. Элементы неопределенности, свойственные случайным явлениям, требуют специальных методов изучения. Разработкой таких методов и занимается теория вероятностей. Начало теории вероятностей положено работами французских ученых П. Ферма и Б. Паскаля в XVII в. Эти работы представляли собой попытки создания теории азартных игр. Дальнейшими успехами теория вероятностей обязана Я. Бернулли, А. Муавру, П. Лапласу, К. Гауссу, С. Пуассону (XVII – XIX вв). Интенсивное развитие теории вероятностей началось в XIX в. В настоящее время методы теории вероятностей применяются в различных областях практической деятельности: теории надежности, теории массового обслуживания, теоретической физике, астрономии, теории автоматического управления, экономике и др. Теория вероятностей служит также для обоснования математической и прикладной статистик.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Классификация событий Случайным событием (событием) называется любой факт, который в результате испытания может произойти или не произойти, т. е. это возможный исход испытания. Например, события: выпадение герба при бросании монеты; попадание в цель при выстреле; выигрыш по лотерейному билету. События обозначаются: А, В, С, … (заглавными буквами латинского алфавита) или А1, А2, А3, … Событие называется достоверным, если оно обязательно должно произойти в результате испытания. Например, если предприятие выпускает только качественную продукцию, то выход качественного изделия с конвейера предприятия – достоверное событие. Событие называется невозможным, если в результате испытания оно вообще не может произойти. Например, в предыдущем примере невозможным событием является выход с конвейера предприятия бракованного изделия. События называются равновозможными, если в результате испытания ни одно из этих событий не является объективно более возможным. События называются несовместимыми (несовместными), если наступление одного из них исключает наступление любого другого. В противномслучае события называются совместимыми (совместными). Например, если бросают кубик, и событие А – появление 1, а событие В – появление 4, то А и В – несовместные события. Пусть А – некоторое событие, будем обозначать События События События образуют полную группу попарно несовместимых исходов, если в результате испытания обязательно должно произойти одно и только одно из этих событий. Например, если при сдаче экзамена студент получил «неудовлетворительно» (событие
1.2. Классическое и статистическое определения вероятности Пусть исходы некоторого испытания образуют полную группу равновозможных, попарно несовместимых событий. Исход называется благоприятствующим событию А, если появление этого исхода влечет за собой появление события А. Пусть Классическое определение вероятности. Вероятностью события А называется отношение числа исходов, благоприятствующих А, к общему числу равновозможных исходов, т. е.
где Классическое определение вероятности (1.1) следует рассматривать не как определение, а как метод вычисления вероятностей для испытаний, сводящихся к схеме случаев. Общее определение вероятности дано академиком А.Н. Колмогоровым в 1933 г. в книге «Основания теории вероятностей». Это определение сложно, поэтому мы будем пользоваться частным случаем этого определения – классической формулой (1.1). Правила теории вероятностей, основанные на классическом определении, остаются верными и в общем случае. Например: 1) испытание – бросание монеты 1 раз. Найти вероятность выпадения герба Полная группа равновозможных попарно несовместимых исходов –
2) Испытание – бросание 2-х монет. Найти вероятность выпадения двух гербов Заметим, что группа событий Полная группа – Тогда Это означает, если испытание повторять много раз в одинаковых условиях, то с большой точностью событие наступит в 25% случаев. В этом состоит реальный смысл понятия «вероятность». На этом основано статистическое определение вероятности. Статистической вероятностью события А называется относительная частота появления этого события в n проведенных испытаниях:
где m – число испытаний, в которых появилось событие А; n – общее число проведенных испытаний. В отличие от классического определения, статистическое определение вероятности
Свойства вероятности 1. Вероятность любого события заключена между единицей и нулем:
где А – любое событие. 2. Вероятность достоверного события (будем обозначать его
3. Вероятность невозможного события (будем обозначать его знаком пустого множества Æ) равна нулю: P (Æ) = 0. Пример. В начале XVII века один игрок в кости обратился к Галилею с вопросом. Он заметил, что если бросать три кости, то сумма очков 10 появляется несколько чаще, чем сумма 9. Между тем, рассуждал игрок, обе суммы могут быть набраны одинаковым числом способов, а именно:
– 6 способов,
– 6 способов. Отсюда игрок заключил, что вероятности получить сумму 9 и 10 должны быть одинаковы, что противоречит его опыту. Ответ на этот вопрос Галилей опубликовал в статье «О выходе очков при игре в кости» в 1655 г. В чем не прав был игрок? И как правильно найти вероятности получить сумму 9 и сумму 10? Решение Испытание – бросают три кубика. Тогда {111, 112, 113,…, 116, 121,…, 126, …, 666} – полная группа равновозможных попарно несовместимых исходов этого испытания. Общее число таких исходов Ошибка игрока в том, что он рассматривал неравновозможные исходы. Например, исход 1+2+6 наступает в два раза чаще, чем исход 1+4+4; сумме 1+2+6 соответствуют 6 исходов: 126, 162, 216, 261, 612, 621; а сумме 1+4+4 только три исхода: 144, 414, 441. Таким образом Следовательно, Таким образом Элементы комбинаторики Для решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики – раздела математики, изучающего, в частности, вопрос о количестве комбинаций из n элементов по m, которые можно составлять тем или иным способом. Мы рассмотрим три таких способа. Сочетания Комбинации из n элементов по m, отличающиеся только составом, называются сочетаниями. Число сочетаний из n элементов по m равно
где Пример 1. В группе 30 человек. Необходимо выбрать трех делегатов на конференцию. Сколько существует способов это сделать? Решение. Каждый способ – это новая тройка студентов, отобранная из 30 человек. Очевидно, эти тройки отличаются только по составу, то есть являются сочетаниями из 30 элементов по 3. Их количество находится по формуле (1.2):
Пример 2. В шахматном турнире участвует 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия? Решение. Каждая партия играется двумя участниками из 16. Пары игроков отличаются от других пар только составом, то есть представляют собой сочетания из 16 элементов по 2. По формуле (1.2) найдем:
Размещения Комбинации из n элементов по m, отличающиеся составом или порядком элементов, называются размещениями. Число размещений из n элементов по m равно
Пример 3. В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать? Решение. Каждый способ – это новая тройка студентов, отобранная из 30 человек. Очевидно, эти тройки отличаются как по составу, так и по порядку, то есть являются размещениями из 30 элементов по 3. Их количество находим по формуле (1.3):
Пример 4. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин. Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов, как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов, то есть число размещений из 11 по 5 находим по формуле (1.3):
Перестановки Комбинации из n элементов по n, отличающиеся порядком, называются перестановками. Число перестановок из n элементов равно
Пример 5. Порядок выступления семи участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно? Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, то есть является перестановкой из 7 элементов. Их число находим по формуле (1.4):
Сформулируем важное правило, которое часто применяется при решении комбинаторных задач. Правило произведения. Если элемент А может быть выбран n способами, после каждого такого выбора элемент B может быть выбран m способами, то выбор пары элементов А, В в указанном порядке может быть осуществлен Приведем примеры на вычисление вероятности случайного события с использованием формул комбинаторики. Пример 6. Студенческая группа из 6 девушек и 8 юношей выбирает наудачу 5 человек для участия в конференции. Найти вероятность того, что 1) все выбранные лица оказались юношами; 2) среди выбранных лиц 3 юноши и 2 девушки. Решение. Введем обозначения событий: А – все выбранные лица оказались юношами; В – среди выбранных лиц 3 юноши и 2 девушки. Испытание – выбор случайным образом 5 лиц из 14. Общее число N всех возможных элементарных исходов испытания равно числу способов, которыми можно отобрать 5 человек из 14:
1) Подсчитаем число исходов, благоприятствующих событию А:
так как 5 юношей из 8 можно отобрать Согласно классическому определению вероятности:
2) Событие В состоит в выборе 3 юношей из 8 и 2 девушек из 6. Число исходов, благоприятствующих событию В:
Имеем:
При решении задач подобного типа, когда исходное множество, из которого происходит выбор, делится по составу на две или более групп, удобно использовать схемы (рис. 1.1).
Действия над событиями
Суммой двух событий А и В называется событие А+В, состоящее в наступлении либо события А, либо события В, либо обоих событий вместе. Например, если аудитор проверяет отчеты двух предприятий и А – отчет первого предприятия выполнен верно, В – отчет второго предприятия выполнен верно, то А + В – отчет хотя бы одного из двух предприятий выполнен верно. В частности, если события А и В – несовместны (наступление одного из них исключает наступление другого), то событие А + В состоит в появлении любого из этих событий. Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий (одного или более). Произведением двух событий А и В называется событие АВ, состоящее в совместном наступлении события А и события В. Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий. Например,случайным образом выбираем точку в прямоугольнике D. Пусть событие А – попадание точки в область А, В – попадание точки в область В. Тогда событие А + В – попадание точки в заштрихованную область (рис. 1.6); событие
Доказательство
Формула полной вероятности является следствием двух основных теорем – теоремы сложения вероятностей и теоремы умножения вероятностей. Заметим, что вероятности Пример 2. В торговую фирму поступили телевизоры от трех поставщиков в количественном отношении 1: 4: 5. Практика показала, что телевизоры, поступившие от I, II, III поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98%, 88% и 92% случаев. Найти вероятность того, что наугад купленный в фирме телевизор не потребует ремонта в течение гарантийного срока. Решение.
А – телевизор не потребует ремонта в течение гарантийного срока.
По формуле полной вероятности (1.14):
Следствием теоремы умножения и формулы полной вероятности является теорема гипотез или формула Байеса по имени автора этой теоремы. Рассмотрим следующую задачу. Имеется полная группа несовместных гипотез
Решение задачи. По теореме умножения вероятностей (1.7) имеем:
Отсюда
с учетом формулы полной вероятности (1.14):
Формула (1.15) называется формулой Байеса или теоремой гипотез. Пример 3. В условиях предыдущего примера о телевизорах известно, что проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор? Решение.
По формуле (1.15):
Итак, после наступления события Пример 4. Объект может находиться в двух различных состояниях Практикой установлено, что приблизительно 30% времени объект находится в состоянии Какому из сообщений следует больше доверять? Решение. Доверять следует тому сообщению, вероятность которого больше. Введем обозначения событий:
По условию задачи Событие А – станция № 1 сообщила, что объект находится в состоянии
событие
По формуле Байеса (1.15) имеем:
Ответ: из двух переданных сообщений более правдоподобно сообщение станции № 1.
В схеме повторных испытаний В последнем примере мы видим, что есть значения k (в данном случае Теорема. Наивероятнейшее число
причем таких Доказательство: 1. Докажем, что таких
Так как 2. По определению наивероятнейшего числа:
Из неравенства (1) с учетом формул Бернулли и числа сочетаний имеем:
После почленного деления на
Умножая обе части неравенства на выражение
Отсюда
Аналогично из неравенства (2) системы получаем Пример 1. В условиях примера п. 1.8
Так как
Пример 2. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее число выпадений трёх очков было равно 10? Решение. Пусть событие Наивероятнейшее число успехов
Отсюда
Вычислений
Если число испытаний Теорема 1. Формула Пуассона. Если вероятность успеха в каждом испытании стремится к нулю
Эта приближенная формула дает незначительные погрешности, если
Пример 1. Швейной фабрикой выпускаются два вида пальто с меховым воротником и без него. Пальто с меховым воротником составляют 0,01% от всего объема выпускаемых изделий. Найти вероятность того, что из 100 тыс. пальто, изделий с меховым воротником окажется только два. Решение. В этом примере n достаточно велико: Пусть событие А – пальто с меховым воротником, тогда вероятность успеха Параметр, Тогда по формуле Пуассона (1.18):
Ответ: примерно в 0,2% случаев из 100 тыс. пальто два окажутся с меховым воротником.
Правую часть приближенной формулы можно рассматривать как функцию двух переменных
Эта функция называется функцией Пуассона, для нее существуют таблицы (см. табл. П.3). Пример 2. На факультете насчитывается 1825 студентов. Какова вероятность, что 1 сентября является днем рождения одновременно четырех студентов? Решение. Из условия задачи
Следствие 1
Доказательство:
Следствие 2
Доказательство:
Пример 7. Сколько нужно провести опытов, чтобы с вероятностью 0,901 утверждать, что частота интересующего нас события будет отличаться по абсолютной величине от вероятности появления этого события, равной 0,4, не более чем на 0,1? Решение. Если
Отсюда
По таблицам значений функции Лапласа (табл. П. 2), по значению Ф(х) = 0,4505, находим значение аргумента х:
Так как Отсюда имеем С учетом целочисленности n получаем Итак, нужно провести не менее 66 опытов, чтобы с вероятностью 0,901 частота интересующего нас события отличалась по абсолютной величине от вероятности появления этого события не более, чем на 0,01.
Упражнения для самопроверки 1. Два букиниста обмениваются друг с другом парами книг. Найти число способов обмена, если первый букинист обменивает 6 книг, а второй – 8 книг. Ответ: 588
2. Абонент забыл две промежуточные цифры номера телефона и набрал их наугад. Найти вероятность того, что номер набран правильно в случаях: а) две разные цифры расположены в номере рядом; б) обе цифры расположены в разных местах, за исключением первой позиции. Ответ: а) 1/45; б) 0,01
3. В урне 40 шаров: 15 белых, 15 красных и 10 синих. Найти вероятность появления цветного шара. Ответ: 0,47
4. Абонент забыл первую цифру телефонного номера. Найти вероятность того, что при наборе номера наудачу он наберет его верно не более чем с трёх попыток. Ответ:0,38
5. В лотерее разыгрывается 200 вещевых и 50 денежных выигрышей на каждые 10 тыс. билетов. Чему равна вероятность выигрыша вообще? Ответ: 0,025
6. В читальном зале имеется 6 учебников, из которых три нового выпуска. Читатель последовательно, один за другим, взял два учебника. Найти вероятность того, что обе взятые книги нового выпуска. Ответ: 0,2
7. В автохозяйстве имеются две автоцистерны. Вероятность технической неисправности этих машин составляет соответственно 0,9 и 0,8. Найти вероятность исполнения работы второй автоцистерной заказчику, сделавшему накануне заказ на автоцистерну. Ответ: 0,4
8. Инвестор решил вложить поровну средства в три предприятия при условии возврата ему через определенный срок 150% от вложенной суммы каждым предприятием. Вероятность банкротства каждого из предприятий 0,2. Найти вероятность того, что по истечении срока кредитования инвестор получит обратно, по крайней мере, вложенную сумму. Ответ: 0,896 9. Три стрелка выстрелили залпом по цели, и две пули поразили её. Найти вероятность того, что первый стрелок поразил цель, если вероятности попада
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1083; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.016 с.) |

 – событие, противоположное событию А, т. е. событие, состоящее в ненаступлении события А.
– событие, противоположное событию А, т. е. событие, состоящее в ненаступлении события А. и
и  называются независимыми, если наступление или ненаступление одного из них не влияет на наступление или ненаступление другого.
называются независимыми, если наступление или ненаступление одного из них не влияет на наступление или ненаступление другого. – студент получил «отлично», тогда
– студент получил «отлично», тогда  } – полная группа событий.
} – полная группа событий. – полная группа равновозможных, попарно несовместимых элементарных исходов некоторого испытания.
– полная группа равновозможных, попарно несовместимых элементарных исходов некоторого испытания. , (1.1)
, (1.1) – вероятность события А;
– вероятность события А; 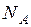 – число исходов, благоприятствующих А;
– число исходов, благоприятствующих А;  – общее число исходов.
– общее число исходов. .
. ,
,  . Тогда
. Тогда  .
.
 не образуют полную группу попарно несовместимых равновозможных исходов, т. к. событие г + ц наступает в два раза чаще события 2 г или события 2 ц.
не образуют полную группу попарно несовместимых равновозможных исходов, т. к. событие г + ц наступает в два раза чаще события 2 г или события 2 ц.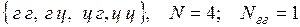 .
. .
. ,
,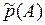 является опытной характеристикой.
является опытной характеристикой. ,
, (омега)) равна единице
(омега)) равна единице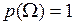 .
. –
–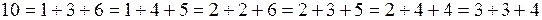 –
– .
. , а
, а 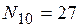 .
. ,
, 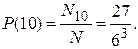
 , что соответствует наблюдениям игрока.
, что соответствует наблюдениям игрока.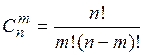 , (1.2)
, (1.2)
 способов.
способов. партий.
партий. . (1.3)
. (1.3) способов.
способов. вариантов.
вариантов. (1.4)
(1.4)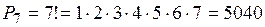 вариантов.
вариантов. способами.
способами. .
. ,
, способами.
способами.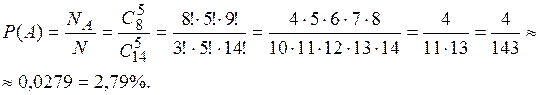
 .
.

 – попадание случайной точки в область d, которая выделена на рис.1.7 штриховкой.
– попадание случайной точки в область d, которая выделена на рис.1.7 штриховкой. На теоретико-множественном языке сумме событий А+В соответствует объединение множеств
На теоретико-множественном языке сумме событий А+В соответствует объединение множеств  ; произведению событий
; произведению событий  соответствует пересечение множеств
соответствует пересечение множеств 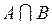 .
.
 , что и требовалось доказать.
, что и требовалось доказать.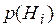 н е в с е г д а о д и н а к о в ы.
н е в с е г д а о д и н а к о в ы. – телевизор поступил от i-го поставщика,
– телевизор поступил от i-го поставщика,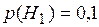 ;
;  ;
; 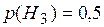 .
. ;
; 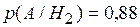 ;
;  .
. .
. . Вероятности этих гипотез до опыта известны и равны
. Вероятности этих гипотез до опыта известны и равны  . Известно, что испытание проведено и событие А наступило. С учетом этой дополнительной информации необходимо произвести количественную переоценку гипотез, т. е. найти
. Известно, что испытание проведено и событие А наступило. С учетом этой дополнительной информации необходимо произвести количественную переоценку гипотез, т. е. найти .
.
 ,
, . (1.15)
. (1.15)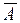 – телевизор потребует ремонта,
– телевизор потребует ремонта,  .
.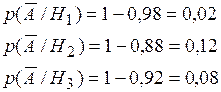
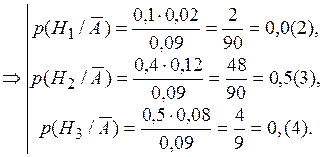
 увеличилась с 0,4 до 0,5(3), а гипотез
увеличилась с 0,4 до 0,5(3), а гипотез  ,
,  уменьшилась от 0,1 до 0,0(2), от 0,5 до 0,(4) соответственно. После поступления дополнительной информации о наступлении события
уменьшилась от 0,1 до 0,0(2), от 0,5 до 0,(4) соответственно. После поступления дополнительной информации о наступлении события  и
и  , случайно переходя из одного состояния в другое.
, случайно переходя из одного состояния в другое.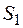 , а станция № 2 – объект находится в состоянии
, а станция № 2 – объект находится в состоянии  – объект в состоянии
– объект в состоянии  .
.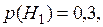

 – станция № 1 не ошиблась, а № 2 ошиблась и
– станция № 1 не ошиблась, а № 2 ошиблась и ;
;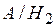 – станция № 1 ошиблась, а № 2 – не ошиблась и
– станция № 1 ошиблась, а № 2 – не ошиблась и .
.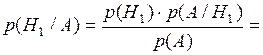

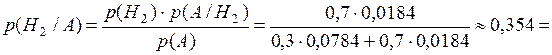

 ), обладающие наибольшей вероятностью
), обладающие наибольшей вероятностью 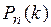 . Число
. Число  наступления события А в
наступления события А в  независимых испытаниях называется наивероятнейшим, если
независимых испытаниях называется наивероятнейшим, если 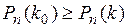 , для
, для 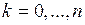 .
. , (1.17)
, (1.17)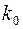 не более двух.
не более двух. , длина этого промежутка равна
, длина этого промежутка равна

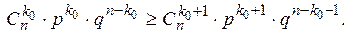
 получим
получим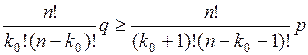 .
. , после упрощений получим неравенство
, после упрощений получим неравенство или
или 


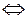
 .
. , т. к.
, т. к.  .
. . Из полученных оценок для
. Из полученных оценок для 


 . Наивероятнейшее число
. Наивероятнейшее число 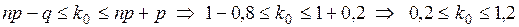 .
.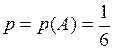 ,
,  .
.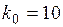 , найдем общее число испытаний
, найдем общее число испытаний  по оценке (1.17):
по оценке (1.17):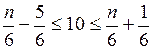 или
или 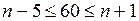 .
. , т. е. для того, чтобы наивероятнейшее число выпавших троек было равно 10, необходимо подбросить игральную кость от 59 до 65 раз.
, т. е. для того, чтобы наивероятнейшее число выпавших троек было равно 10, необходимо подбросить игральную кость от 59 до 65 раз.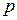 и
и  – дробные числа. Поэтому рассмотрим приближенные формулы вычисления
– дробные числа. Поэтому рассмотрим приближенные формулы вычисления  .
. при неограниченном увеличении числа испытаний
при неограниченном увеличении числа испытаний 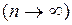 и произведении
и произведении 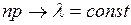 , то вероятность
, то вероятность 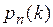 удовлетворяет следующему соотношению:
удовлетворяет следующему соотношению: . (1.18)
. (1.18) .
. .
. =
= 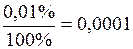 .
.
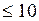 .
. .
. :
: .
. ,
,  ,
, 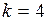 .
. .
.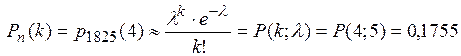 (табл. П. 3).
(табл. П. 3). . (1.21)
. (1.21)

 . (1.22)
. (1.22)

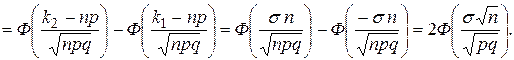
 , то
, то  . Используя условие задачи и следствие 2, получаем:
. Используя условие задачи и следствие 2, получаем: .
.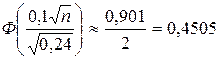 .
. , т.е.
, т.е.  .
. , то
, то  .
. ,
,  , следовательно
, следовательно 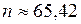 .
. .
.


