Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел I. Элементы линейной алгебры
Тема 1. Матрицы и определители Основные сведения о матрицах. Операции над матрицами. Определители квадратных матриц. Определители n-го порядка. Разложение определителя по строке (столбцу) (теорема Лапласа.). Свойства определителей.
Тема 2. Системы линейных алгебраических уравнений Основные понятия и определения. Обратная матрица. Системы n линейных уравнений с n переменными. Решение системы n линейных алгебраических уравнений методом Гаусса. Решение систем n линейных алгебраических уравнений с n неизвестными по правилу Крамера. Решение матричных уравнений с помощью обратной матрицы.
Тема 3. Основные задачи аналитической геометрии Различные виды уравнений прямой. Нахождение расстояния от точки до прямой. Основные типы кривых и их канонические уравнения. Построение кривых по каноническим уравнениям. Построение линий в полярной системе координат и линий, заданных параметрически. Плоскость. Основные уравнения плоскости. Нахождение расстояния от точки до плоскости. Прямая линия в пространстве. Совместное расположение прямой и плоскости в пространстве. Поверхности второго порядка. Типы поверхностей и их канонические уравнения. Построение поверхностей. Раздел 2. Основы математического анализа Тема 4. Пределы и непрерывность Числовые последовательности. Предел числовой последовательности. Предел функции в точке и на бесконечности. Бесконечно малые и бесконечно большие функции. Свойства предела функции. Односторонние пределы. Пределы монотонных функций. Замечательные пределы. Непрерывность функции в точке. Локальные свойства непрерывных функций. Точки разрыва и их классификация. Тема 5. Дифференциальное исчисление Понятие производной, ее геометрический, механический и экономический смысл. Формулы дифференцирования основных элементарных функций. Правила дифференцирования суммы, разности, произведения, частного и суперпозиции функций. Производные высших порядков. Дифференциал функции, его геометрический смысл. Связь непрерывности и дифференцируемости функции. Применение дифференциала в приближенных вычислениях. Приложение дифференциального исчисления. Возрастание и убывание функции. Экстремум функции. Наибольшее и наименьшее значение функции на отрезке и интервале. Выпуклость функции. Точки перегиба. Асимптоты графика функции. Общая схема исследования функции и построения их графиков.
Тема 6. Интегральное исчисление Первообразная функция. Неопределенный интеграл, его свойства. Таблица интегралов. Существование неопределенного интеграла. Интегрирование элементарных функций. Методы интегрирования: непосредственное, замена переменной, интегрирование по частям. Интегрирование некоторых классов функции: рациональных дробей, иррациональных и тригонометрических функций. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральной суммы, его основные свойства. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов. Методы интегрирования заменой переменной и по частям в определенном интеграле. Приложения интеграла к вычислению площадей плоских фигур. Использование определенного интеграла в экономике. Раздел 3. Основы теории вероятностей и математической статистики Тема 7. Элементы комбинаторики Основные теоремы комбинаторики. Основные правила комбинаторики. Комбинации объектов. Размещения. Сочетания. Перестановки. Тема 8. Основы теории вероятностей Испытания, события, виды событий, система элементарных событий. Классическое и статистическое определения вероятности. Теоремы сложений вероятностей несовместимых и совместимых событий. Теоремы умножения вероятностей независимых и зависимых событий. Противоположенные события. Вероятность появления только одного и хотя бы одного из независимых событий. Формула полной вероятности. Формула Байеса. Понятие случайных величин, их виды. Закон распределения дискретной случайной величины. Основные характеристики дискретной случайной величины и их смысл: математическое ожидание, дисперсия и среднее квадратическое отклонение. Свойства математического ожидания и дисперсии. Наиболее распространенные законы распределения вероятностей. Тема 9. Элементы математической статистики Задачи математической статистики. Способы отбора статистических данных. Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма. Средние величины. Основные свойства средней арифметической. Показатели вариации. Основные свойства дисперсии. Упрощенный способ расчета средней арифметической и дисперсии. Выборочный метод. Статистическое оценивание и проверка гипотез, статистические методы обработки экспериментальных данных.
IV.Литература Основная литература Рау В.Г. Практический курс математики и статистики. – М.: Высшая школа, 2006.
Дополнительная литература
Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии.— М.: Наука, 1984. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисле-ние.— М.: Наука, 1988. Бугров Я.С., Никольский С.М. Высшая математика: Задачник.— М.: Нау-ка,1982. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах.— М.: Наука, Физмат-лит,2000. ВентцельА.Д. Курс теории случайных процессов.— М.: Наука, 1993. Гмурман В.Е. Руководство к решению задач по теории вероятностей и мате-матической статистике.— М.: Высшая школа, 1998. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнени-ях и задачах. — М.: Высшая школа, 2001. Ильин В.А., Куркина А.В. Высшая математика. – М.: Проспект, 2004. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая ста-тистика.— М.: Высшая школа, 1982. Кудрявцев Л.Д. Краткий курс математического анализа. Т. 1, 2.-Альфа, 1998. Минорский В.П. «Сборник задач по высшей математике». М., Наука, 1987г. Сборник задач по математике для втузов. /Под ред. А.В. Ефимова.- М.: Нау-ка.-Ч.1-2, 1993-1994. Турецкий В.Я. Математика и информатика. – 3-е изд. – М.: ИНФРА-М, 2005. Шипачев В.С. «Задачи по высшей математике». М.: Высшая школа, 1997. Интернет-ресурсы
http://spcpa.ru/learning/zao/v8.html http://sbiryukova.narod.ru/Met_pos_04-05/Ogl_tem.htm#H http://www.refcity.ru/info/49.html http://alexlarin.narod.ru/kvm.html http://pmi.ulstu.ru/a/matan/lek11.html http://www.ispu.ru/library/math/sem1/kiselev1/node33.html http://do.rksi.ru/library/courses/ms/book.dbk V.Перечень вопросов и типовых заданий для промежуточной аттестации Вопросы
1. Основные сведения о матрицах. Виды матриц и действия над ними. 2. Определители матриц и способы их вычисления. 3. Обратная матрица. 4. Системы линейных уравнений. Представление системы линейных уравнений в матричном виде. 5. Решение системы линейных алгебраических уравнений методом обратной мат-рицы. 6. Решение системы линейных алгебраических уравнений методом Крамера. 7. Решение системы линейных алгебраических уравнений методом Гаусса. 8. Предел числовой последовательности и предел функции. Свойства предела функции. 9. Односторонние пределы. Замечательные пределы. 10. Бесконечно малые и бесконечно большие величины. 11. Непрерывность функции в точке и на отрезке. Свойства функции непрерывной на отрезке. 12. Точки разрыва и их классификация. 13. Определение производной, ее геометрический и механический смысл. 14. Основные правила дифференцирования функций. 15. Производные основных элементарных функций. Производная сложной функции. 16. Производные высших порядков. 17. Дифференциал функции, его геометрический смысл. 18. Применение дифференциала в приближенных вычислениях. 19. Первообразная. Неопределенный интеграл. Таблица основных интегралов. 20. Основные свойства неопределенного интеграла. 21. Основные методы интегрирования: метод замены переменной в неопределенном интеграле.
22. Основные методы интегрирования: метод интегрирования неопределенного ин-теграла по частям. 23. Определенный интеграл и его свойства. Геометрический смысл определенного интеграла. 24. Теорема Ньютона-Лейбница. 25. Замена переменной и вычисление по частям в определенном интеграле. 26. Операции над событиями. Теорема сложения вероятностей. 27. Теорема умножения вероятностей. 28. Понятие гипотезы. Формула полной вероятности. 29. Априорная и апостериорная вероятность. Формула Байеса. 30. Случайная величина. Функция распределения случайных величин. 31. Дискретные случайные величины. Свойства функции распределения дискретных случайных величин. Ряд и многоугольник распределения. 32. Понятие закона распределения дискретной случайной величины. Опыт Бернулли. 33. Непрерывная случайная величина и ее плотность распределения. 34. Равномерное распределение. Нормальное распределение. 35. Понятие математического ожидания. Формулы для математических ожиданий дискретных случайных величин и непрерывных случайных величин. 36. Дисперсия. Свойства дисперсии и среднего квадратического отклонения. Форму-лы для дисперсии дискретных случайных величин и непрерывных случайных ве-личин. 37. Понятие моментов. Мода и медиана случайной величины. 38. Функция распределения и плотность распределения двумерной случайной вели-чины и ее свойства. 39. Неравенство Чебышева. Теорема Чебышева. 40. Центральная предельная теорема для одинаково распределенных слагаемых. Теорема Ляпунова. Типовые задания
Элементы высшей алгебры Пример 1. Для заданной системы трех линейных уравнений с тремя неизвестными Требуется: 1) найти ее решение с помощью формул Крамера 2) записать систему в матричной форме и решить ее средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение; 3) решить систему методом Гаусса (методом последовательного исключения неизвестных). ( Для решения Вы можете использовать программу MS Excel. Рекомендации по ее применению находятся в конце пособия); Решение: 1) Метод Крамера. Решение системы находим по формулам Крамера: Вычисляем определители системы: · главный определитель системы
Система совместна, так как главный определитель системы не равен нулю.
· дополнительные определители системы:
Подставляя значения определителей в формулы Крамера, получаем:
Проверка:
2) Метод Гаусса (или метод последовательного исключения неизвестных). Составим расширенную матрицу системы и приведем ее к треугольному виду:
Заданная система уравнений приведена к виду:
Найдем корни системы уравнений:
3) Решение системы средствами матричного исчисления. Запишем заданную систему уравнений в матричном виде
где Тогда ее решение имеет вид Определитель системы D равен:
Таким образом обратная матрица Составим обратную матрицу
где
Обратная матрица системы имеет вид:
Проверим правильность вычисления обратной матрицы, используя матричное умножение, т. е. покажем, что Вычислим
Найдем решение системы:
Ответ:
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.226 (0.012 с.) |
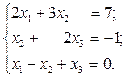


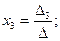 где
где 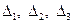 - (дополнительные) определители третьего порядка, получаемые из главного определителя системы
- (дополнительные) определители третьего порядка, получаемые из главного определителя системы 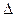 заменой 1 -, 2 – или 3 – столбца соответственно на столбец свободных членов
заменой 1 -, 2 – или 3 – столбца соответственно на столбец свободных членов 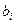 .
.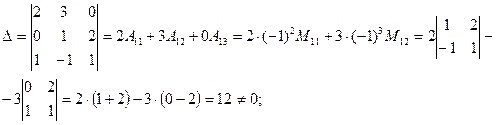
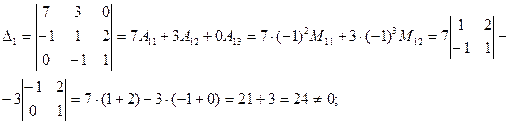

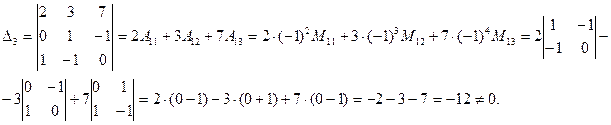
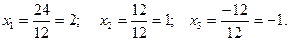
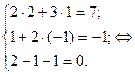
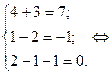
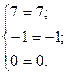
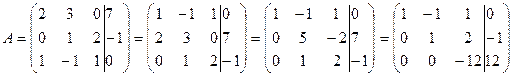 .
.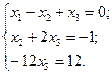 .
.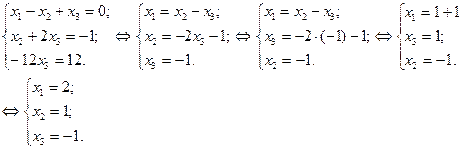
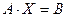 ,
,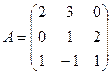 ,
, 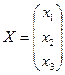 ,
, 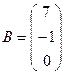 .
. если определитель системы отличен от нуля.
если определитель системы отличен от нуля.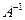 существует и система имеет единственное решение.
существует и система имеет единственное решение.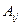 элемента
элемента  и запишем матрицу
и запишем матрицу 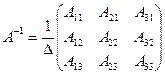 ,
,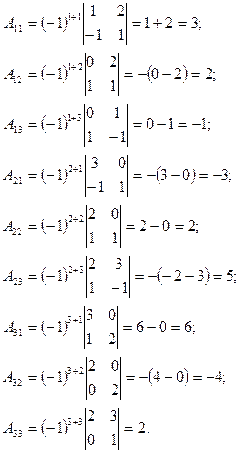

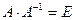 , где Е - единичная матрица.
, где Е - единичная матрица.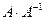
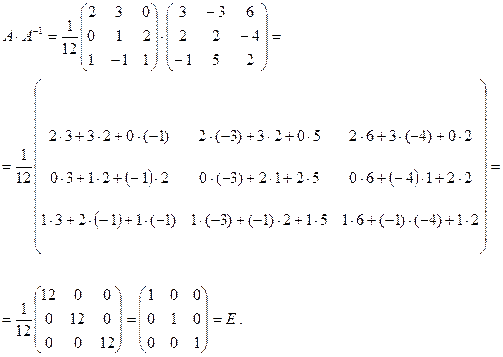
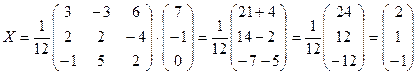
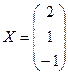 или
или