
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы линейной алгебры и аналитической геометрииСодержание книги
Поиск на нашем сайте
Математика
Южно-Сахалинск 2011
СОДЕРЖАНИЕ
4.1. Модуль 1 4.1.1.Тематический план модуля 1……………………………………4 4.1.2. Содержание программы модуля 1…………………………….5 4.1.3 Тест………………………………………………………………….5 4.1.4 Примерные задания контрольной работы №1………………6 4.1.5 Вопросы для оценки качества освоения модуля 1……….. 6 4.2 Модуль 2 4.2.1 Тематический план модуля 2……………………………………7 4.2.2 Содержание программы модуля 2……………………………..7 4.2.3 Тест ………………………………………………………………….8 4.2.4 Примерные задания контрольной работы №2……………….9 4.2.5 Вопросы для оценки качества освоения модуля 2 ………..10 4.3 Модуль 3 4.3.1 Тематический план модуля 3 ………………………………….10 4.3.2 Содержание программы модуля 3……………………………11 4.3.3 Примерные задания контрольной работы №3……………...11 4.3.4 Вопросы для оценки качества освоения модуля 3………..12 4.4 Модуль 4 4.4.1 Тематический план модуля 4 …………………………………..12 4.4.2 Содержание программы модуля 4…………………………….13 4.4.3 Тест…………………………………………………………………14 4.4.4 Примерные задания контрольной работы №4……………...15 4.4.5 Вопросы для оценки качества освоения модуля 4 ………..15 5. Виды аттестации по семестрам…………………………………………………………….16 6. Итоговый тест по дисциплине……………………………………………………………….17 7. Оценка удовлетворенности качеством обученияпо дисциплине…………………….18 8. Учебно-методическое и информационное обеспечение дисциплины……………….19
Программа дисциплины «математика» 1. Цель освоения дисциплины: формирование у студентов математической культуры; основных понятий по математике, необходимых в практической профессиональной деятельности; понимания математической составляющей в общей подготовке специалиста в профессиональной области.
Задачи дисциплины: развитие логического мышления, привитие навыков корректного употребления математических понятий и символов для выражения различных количественных и качественных отношений; 2. Место дисциплины в структуре ОПП: Математика играет все возрастающую роль в естественнонаучных и гуманитарных исследованиях. Являясь универсальным языком науки, математика позволяет не только осуществлять различные количественные расчеты, но и является средством предельно четкой формулировки понятий и проблем той или иной отрасли знаний. Математика стала элементом общечеловеческой культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного управленца. Дисциплина «Математика» относится к базовой части математического и естественнонаучного цикла (Б.2.). Освоение дисциплины «Математика» является необходимой основой для изучения модулей дисциплин профессионального цикла. Для освоения дисциплины «Математика» студенты используют знания, умения и виды деятельности, сформированные в процессе изучения предмета «Математика» на предыдущем уровне образования. Учебная дисциплина "Математика" не требует предварительных знаний, выходящих за рамки программы средней общеобразовательной школы.
Процесс изучения дисциплины направлен на формирование элементов следующих компетенций в соответствии с ФГОС ВПО по данному направлению: а) общекультурных (ОК): -владением основными методами количественного анализа и моделирования, теоретического и экспериментального исследования (ОК-4); -умением логически верно, аргументировано и ясно строить устную и письменную речь; (ОК-9); -владением навыками самостоятельной, творческой работы; (ОК-16); -способностью к формированию, поддержанию и использованию конструктивных общефизических и социально-психологических ресурсов, необходимых для здорового образа жизни (ОК-17). б) профессиональных (ПК): -способностью применять адекватные инструменты и технологии регулирующего воздействия при реализации управленческого решения (ПК-5);
-способностью адаптировать основные математические модели к конкретным задачам управления (ПК-23); В результате обучения студент должен знать: - основы разделов математики (алгебры и геометрии, математического анализа, теории вероятностей); - основные математические методы и модели принятия управленческих решений - о математическом моделировании простейших экономических и управленческих проблем и содержательно интерпретировать получаемые количественные результаты их решений; - навыки самостоятельной работы и постоянно пополнять свой уровень знаний в свете современных тенденций развития математического инструментария для решения профессиональных задач. Уметь: - решать типовые математические задачи, используемые при принятии управленческих решений; обрабатывать эмпирические и экспериментальные данные; использовать математический язык и математическую символику при построении организационно- управленческих моделей; применять математику к решению конкретных технических задач; - формулировать прикладные проблемы на языке уравнений, систем уравнений, неравенств, графических представлений; - использовать математический аппарат для решения прикладных задач экономики и управления; Владеть: - математическими, статистическими и количественными методами решения типовых профессиональных задач;
Общая трудоемкость дисциплины 5 зачетных единиц (180 часов). Дисциплина изучается 2 семестра (1,2). Всего ЗЕТ- 5, часов -180 (72/108), в том числе: лекции – 36 часов (18+18), практика – 36 часов (18+18), самостоятельная работа – 108 часов, контрольные работы (1-4 модули), долгосрочные задания (1,2,4 модули), коллоквиум (1,2 семестрах). МОДУЛЬ 1 ТЕМАТИЧЕСКИЙ ПЛАН МОДУЛЯ 1 СЕМЕСТР 1
4.1.2. Содержание программы модуля 1 дисциплины ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 4.1.3. Индивидуальное задание (тест 1) МОДУЛЬ 2 ТЕМАТИЧЕСКИЙ ПЛАН МОДУЛЯ 2
4.2.2. Содержание программы модуля 2 дисциплины
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 4.2.3. Индивидуальное задание (тест №2). МОДУЛЬ 3 ТЕМАТИЧЕСКИЙ ПЛАН МОДУЛЯ 3
4.3.2. Содержание программы модуля 3 дисциплины ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ МОДУЛЬ 4 ТЕМАТИЧЕСКИЙ ПЛАН МОДУЛЯ 4
4.4.2. Содержание программы модуля 4 дисциплины
Тема 1 Основные понятия теории вероятностей Основные понятия теории вероятностей. Элементы комбинаторики. Размещения, перестановки, сочетания. Определение случайного события. Операции над случайными событиями.. Полная группа событий. Определения вероятности (классическое, статистическое, геометрическое). Свойства вероятности. Условная вероятность. Независимые и зависимые события. Теоремы сложения и умножения вероятностей. Вероятность наступления хотя бы одного события. Формула полной вероятности. Вероятность гипотез (формула Байеса). Повторные испытания. Формула Бернулли, формула Пуассона, локальная и интегральная теоремы Лапласа.
Тема 2 Случайные величины Случайные величины и способы их описания. Понятие закона распределения вероятностей дискретных случайных величин. Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение, начальные и центральные моменты, асимметрия, эксцесс, мода. Биномиальный закон распределения, закон распределения Пуассона, их числовые характеристики. Функция распределения дискретной случайной величины, построение ее графика. Неравенство Чебышева. Закон больших чисел и его следствие. Задание системы двух дискретных случайных величин, построение законов распределения ее составляющих. Числовые характеристики системы двух дискретных случайных величин: ковариация, коэффициент корреляции. Непрерывные случайные величины. Функция и плотность распределения, их свойства. Вероятность попадания непрерывной случайной величины в интервал. Числовые характеристики непрерывных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение, медиана. Цепи Маркова и их использование в моделировании социально-экономических процессов. Матрица вероятностей перехода (стохастическая матрица). Характеристики цепей Маркова: вероятности перехода между состояниями за конечное число шагов, предельное распределение состояний, условие его существования.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 4.4.3. Индивидуальное задание. «Теория вероятностей и математическая статистика» 1. Сколькими способами можно взять _ 8 _ шаров из корзины, содержащей _ 11 _ шаров. 2. На гору ведут __32_ тропинки. Сколькими способами можно подняться и спуститься с горы, если спуск и подъем происходят по разным дорогам. 3. В первой урне содержится _4__ белых и _2 _ черных шаров. Во второй урне _3_ белых и _ _4 _ черных шаров. Из первой урны вынимают один шар, и перекладывают во вторую, а затем из второй урны вынимают один шар. Найти вероятность того, что этот шар окажется черным. 4. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятности того, что они выйдут из строя соответственно равны: _ 0,15_,__025_ и _0,3_. Найти вероятность того, что выйдет из строя: а) только одно устройство; б) только два устройства; с) все три устройства; г) ни одно устройство. 5. Для того, чтобы сдать экзамен студенту надо ответить на два вопроса билета. Студент знает ответы на _ 16__ вопросов из _ _20. Найти вероятность того, что студент сдаст экзамен.
6. Найти закон распределения дискретной случайной величины Х - числа белых шаров среди двух вынутых из урны, содержащей __ 3 __белых и __5_ черных шара. 7. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения
8. Даны две независимые дискретные случайные величины Х и Y. Закон распределения каждой из величин задан в виде таблицы, в первой строке которой указаны возможные значения случайной величины, а во второй строке – вероятности, с которыми принимаются эти значения. Через хi обозначены возможные значения величины Х, а через уi – значения величины Y. Через p i и Pi обозначены вероятности возможных значений хi и уi. Определить закон распределения случайной величины Z=X+Y. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величин X, Y, Z. 9. 10.
11. Пусть система двух случайных величин имеет таблицу распределения:
Найти: а) законы распределения компонент Х и Y; б) условный закон распределения составляющей Х при условии, что Y=0; в) ковариацию; г) коэффициент корреляции; д) найти вероятность того, что сл. в. Х примет значение, меньшее чем Y. 12. Из генеральной совокупности извлечена выборка объема n=50. Найти
13. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,4,6,7,17. Найти несмещённую оценку математического ожидания 14. Выборочное уравнение парной регрессии имеет вид 15. Найти моду вариационного ряда 1,4,6,7,8,8,9,12. 16. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции 4.4.4. Примерные задания контрольной работы №4
4.4.5. Вопросы для оценки качества освоения модуля 4 дисциплины. ИТОГОВЫЙ ТЕСТ ПО ДИСЦИПЛИНЕ Математика
Южно-Сахалинск 2011
СОДЕРЖАНИЕ
4.1. Модуль 1 4.1.1.Тематический план модуля 1……………………………………4 4.1.2. Содержание программы модуля 1…………………………….5 4.1.3 Тест………………………………………………………………….5 4.1.4 Примерные задания контрольной работы №1………………6 4.1.5 Вопросы для оценки качества освоения модуля 1……….. 6 4.2 Модуль 2 4.2.1 Тематический план модуля 2……………………………………7 4.2.2 Содержание программы модуля 2……………………………..7 4.2.3 Тест ………………………………………………………………….8 4.2.4 Примерные задания контрольной работы №2……………….9 4.2.5 Вопросы для оценки качества освоения модуля 2 ………..10 4.3 Модуль 3 4.3.1 Тематический план модуля 3 ………………………………….10 4.3.2 Содержание программы модуля 3……………………………11 4.3.3 Примерные задания контрольной работы №3……………...11 4.3.4 Вопросы для оценки качества освоения модуля 3………..12 4.4 Модуль 4 4.4.1 Тематический план модуля 4 …………………………………..12 4.4.2 Содержание программы модуля 4…………………………….13 4.4.3 Тест…………………………………………………………………14 4.4.4 Примерные задания контрольной работы №4……………...15 4.4.5 Вопросы для оценки качества освоения модуля 4 ………..15 5. Виды аттестации по семестрам…………………………………………………………….16 6. Итоговый тест по дисциплине……………………………………………………………….17 7. Оценка удовлетворенности качеством обученияпо дисциплине…………………….18 8. Учебно-методическое и информационное обеспечение дисциплины……………….19
Программа дисциплины «математика» 1. Цель освоения дисциплины: формирование у студентов математической культуры; основных понятий по математике, необходимых в практической профессиональной деятельности; понимания математической составляющей в общей подготовке специалиста в профессиональной области. Задачи дисциплины: развитие логического мышления, привитие навыков корректного употребления математических понятий и символов для выражения различных количественных и качественных отношений; 2. Место дисциплины в структуре ОПП: Математика играет все возрастающую роль в естественнонаучных и гуманитарных исследованиях. Являясь универсальным языком науки, математика позволяет не только осуществлять различные количественные расчеты, но и является средством предельно четкой формулировки понятий и проблем той или иной отрасли знаний. Математика стала элементом общечеловеческой культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного управленца. Дисциплина «Математика» относится к базовой части математического и естественнонаучного цикла (Б.2.). Освоение дисциплины «Математика» является необходимой основой для изучения модулей дисциплин профессионального цикла. Для освоения дисциплины «Математика» студенты используют знания, умения и виды деятельности, сформированные в процессе изучения предмета «Математика» на предыдущем уровне образования. Учебная дисциплина "Математика" не требует предварительных знаний, выходящих за рамки программы средней общеобразовательной школы.
Процесс изучения дисциплины направлен на формирование элементов следующих компетенций в соответствии с ФГОС ВПО по данному направлению: а) общекультурных (ОК): -владением основными методами количественного анализа и моделирования, теоретического и экспериментального исследования (ОК-4); -умением логически верно, аргументировано и ясно строить устную и письменную речь; (ОК-9); -владением навыками самостоятельной, творческой работы; (ОК-16); -способностью к формированию, поддержанию и использованию конструктивных общефизических и социально-психологических ресурсов, необходимых для здорового образа жизни (ОК-17). б) профессиональных (ПК): -способностью применять адекватные инструменты и технологии регулирующего воздействия при реализации управленческого решения (ПК-5); -способностью адаптировать основные математические модели к конкретным задачам управления (ПК-23); В результате обучения студент должен знать: - основы разделов математики (алгебры и геометрии, математического анализа, теории вероятностей); - основные математические методы и модели принятия управленческих решений - о математическом моделировании простейших экономических и управленческих проблем и содержательно интерпретировать получаемые количественные результаты их решений; - навыки самостоятельной работы и постоянно пополнять свой уровень знаний в свете современных тенденций развития математического инструментария для решения профессиональных задач. Уметь: - решать типовые математические задачи, используемые при принятии управленческих решений; обрабатывать эмпирические и экспериментальные данные; использовать математический язык и математическую символику при построении организационно- управленческих моделей; применять математику к решению конкретных технических задач; - формулировать прикладные проблемы на языке уравнений, систем уравнений, неравенств, графических представлений; - использовать математический аппарат для решения прикладных задач экономики и управления; Владеть: - математическими, статистическими и количественными методами решения типовых профессиональных задач;
Общая трудоемкость дисциплины 5 зачетных единиц (180 часов). Дисциплина изучается 2 семестра (1,2). Всего ЗЕТ- 5, часов -180 (72/108), в том числе: лекции – 36 часов (18+18), практика – 36 часов (18+18), самостоятельная работа – 108 часов, контрольные работы (1-4 модули), долгосрочные задания (1,2,4 модули), коллоквиум (1,2 семестрах). МОДУЛЬ 1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ТЕМАТИЧЕСКИЙ ПЛАН МОДУЛЯ 1 СЕМЕСТР 1
4.1.2. Содержание программы модуля 1 дисциплины
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.167.10 (0.014 с.) |

 и выборочную дисперсию
и выборочную дисперсию . Какой знак имеет выборочный коэффициент корреляции?
. Какой знак имеет выборочный коэффициент корреляции? и выборочные средние квадратические отклонения
и выборочные средние квадратические отклонения 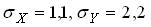 . Тогда выборочный коэффициент регрессии
. Тогда выборочный коэффициент регрессии  на
на  равен…
равен…


