
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3 Элементы математической статистикиСодержание книги
Поиск на нашем сайте
Статистические методы обработки экспериментальных данных. Генеральная и выборочная совокупности, вариационные ряды. Графическое представление вариационных рядов: полигон и гистограмма, эмпирическая функция распределения. Статистические оценки параметров распределения. Генеральная и выборочная средние. Генеральная и выборочная дисперсии. Оценка генеральной дисперсии по исправленной выборочной. Интервальные оценки. Доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения нормального распределения. Проверка статистических гипотез. Нулевая и конкурирующая. Выдвижение гипотезы о характере закона распределения эмпирической выборки. Проверка гипотезы о подчинении эмпирической выборки гипотетическому закону распределения с помощью критерия Пирсона (хи-квадрат). Ковариация, коэффициент корреляции, линейное уравнение регрессии. Проверка гипотезы о значимости выборочного коэффициента корреляции.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 4.4.3. Индивидуальное задание. «Теория вероятностей и математическая статистика» 1. Сколькими способами можно взять _ 8 _ шаров из корзины, содержащей _ 11 _ шаров. 2. На гору ведут __32_ тропинки. Сколькими способами можно подняться и спуститься с горы, если спуск и подъем происходят по разным дорогам. 3. В первой урне содержится _4__ белых и _2 _ черных шаров. Во второй урне _3_ белых и _ _4 _ черных шаров. Из первой урны вынимают один шар, и перекладывают во вторую, а затем из второй урны вынимают один шар. Найти вероятность того, что этот шар окажется черным. 4. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятности того, что они выйдут из строя соответственно равны: _ 0,15_,__025_ и _0,3_. Найти вероятность того, что выйдет из строя: а) только одно устройство; б) только два устройства; с) все три устройства; г) ни одно устройство. 5. Для того, чтобы сдать экзамен студенту надо ответить на два вопроса билета. Студент знает ответы на _ 16__ вопросов из _ _20. Найти вероятность того, что студент сдаст экзамен. 6. Найти закон распределения дискретной случайной величины Х - числа белых шаров среди двух вынутых из урны, содержащей __ 3 __белых и __5_ черных шара. 7. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения
8. Даны две независимые дискретные случайные величины Х и Y. Закон распределения каждой из величин задан в виде таблицы, в первой строке которой указаны возможные значения случайной величины, а во второй строке – вероятности, с которыми принимаются эти значения. Через хi обозначены возможные значения величины Х, а через уi – значения величины Y. Через p i и Pi обозначены вероятности возможных значений хi и уi. Определить закон распределения случайной величины Z=X+Y. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величин X, Y, Z. 9. 10.
11. Пусть система двух случайных величин имеет таблицу распределения:
Найти: а) законы распределения компонент Х и Y; б) условный закон распределения составляющей Х при условии, что Y=0; в) ковариацию; г) коэффициент корреляции; д) найти вероятность того, что сл. в. Х примет значение, меньшее чем Y. 12. Из генеральной совокупности извлечена выборка объема n=50. Найти
13. Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,4,6,7,17. Найти несмещённую оценку математического ожидания 14. Выборочное уравнение парной регрессии имеет вид 15. Найти моду вариационного ряда 1,4,6,7,8,8,9,12. 16. При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции 4.4.4. Примерные задания контрольной работы №4
4.4.5. Вопросы для оценки качества освоения модуля 4 дисциплины.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.27 (0.006 с.) |

 и выборочную дисперсию
и выборочную дисперсию . Какой знак имеет выборочный коэффициент корреляции?
. Какой знак имеет выборочный коэффициент корреляции? и выборочные средние квадратические отклонения
и выборочные средние квадратические отклонения 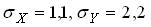 . Тогда выборочный коэффициент регрессии
. Тогда выборочный коэффициент регрессии  на
на  равен…
равен…


