
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория вероятностей и элементы математической статистикиСодержание книги
Поиск на нашем сайте
УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС
Институты: все. Укрупненные группы специальностей и направлений подготовки: 080000 –Экономика и управление 140000 – Энергетика, энергетическое машиностроение и электротехника 150000 – Металлургия, машиностроение и материалообработка 190000 – Транспортные средства 200000 – Приборостроение и оптотехника 210000 – Электронная техника, радиотехника и связь 220000 – Автоматика и управление 230100 – Информатика и вычислительная техника 240000 – Химическая и биотехнологии. Направления подготовки высшего профессионального образования: 261000 – Технология художественной обработки материалов 280200 – Защита окружающей среды Санкт-Петербург Издательство СЗТУ УДК 519.2.06(07)
Математика. Часть 2. Теория вероятностей и элементы математической статистики: учебно-методический комплекс / сост. В.С. Ходоровская. - СПб.: Изд - во CЗТУ, 2008. – с.
Учебно-методический комплекс разработан в соответствии с государственными образовательными стандартами высшего профессионального образования. Дисциплина предусматривает изучение понятий и варианты расчета вероятностей случайных событий, случайных величин и их характеристик, рассматриваются элементы математической статистики и варианты проверки различных гипотез, выдвигаемых при работе со случайными величинами. Приводятся теоретические основы и разбираются варианты решения задач, формулируются тестовые вопросы к рассматриваемым темам. Рассмотрено на заседании кафедры информатики и прикладной математики 22 декабря 2008 г., одобрено методической комиссией факультета общепрофессиональной подготовки 22 декабря 2008 г.
ã Ходоровская В.С., Бессонова Т.Д., Ткаченко Г.Г., Шабаева М.Б., 2009 1. Информация о дисциплине Содержание курса «Теория вероятностей и элементы математической статистики» определяется государственным стандартом, рабочей программой и тематическим планом.
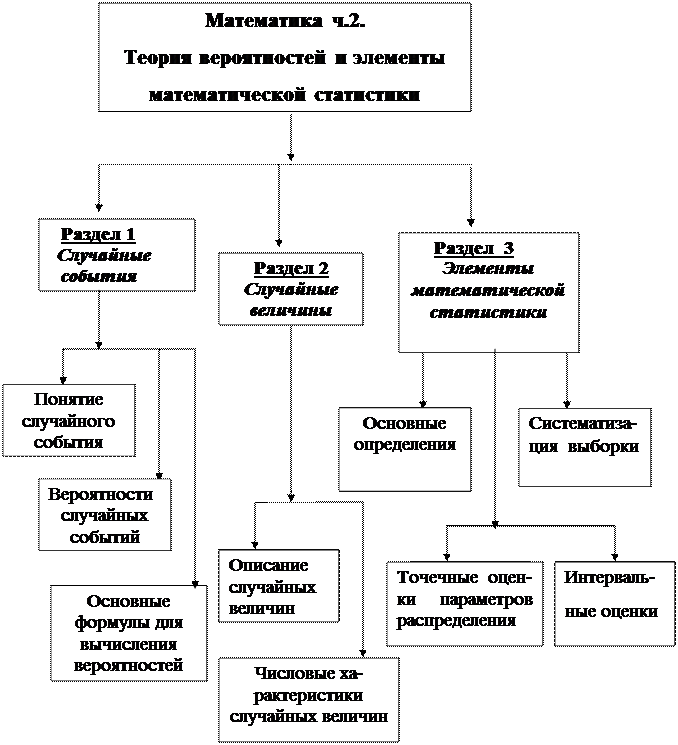
Данная дисциплина изучается студентами на 2-м или 3 курсе в течение семестра. Программа курса включает изучение трех основных теоретических разделов: 1) случайные события; частота и вероятность; основные формулы для вычисления вероятностей, 2) случайные величины; числовые характеристики дискретной и непрерывной случайных величин; нормальный закон распределении, 3) элементы математической статистики, генеральная совокупность и выборка; оценки параметров; корреляция и регрессия, содержание которых представлено в виде структурно-логической схемы на рис. 2.1. Кроме того, включен раздел с указаниями по выполнению лабораторных работ и раздел с методическими указаниями по выполнению контрольной работы. Изучение курса заканчивается выполнением контрольной работы, ответом на вопросы тестов и сдачей экзамена. 1.1. Предисловие Учебно-методический комплекс Математика ч.2 “Теория вероятностей и элементы математической статистики” предназначен для всех форм обучения студентов всех специальностей подготовки высшего профессионального образования. Программой курса предусматривается изучение случайных событий и случайных величин, приводятся формулы, позволяющие производить расчет вероятностей различных случайных событий, находить характеристики случайных величин и определять их законы распределения, рассматриваются элементы математической статистики. Данная дисциплина изучается студентами в течение одного семестра. Рабочая программа включает изучение разделов по темам: «Случайные события», “ Случайные величины“, “Элементы математической статистики“. План практических занятий предусматривает изучение тем: 1. Случайные события, частота и вероятность. Классическое определение вероятности. Условные вероятности. 2. Основные формулы для вычисления вероятностей: схема Бернулли, полной вероятности и Байеса. 3. Случайные величины. Числовые характеристики дискретной и непрерывной случайных величин. В план выполнения лабораторных работ входят темы: 1. Генеральная совокупность и выборка. Обработка выборочных данных. Точечные и интервальные оценки параметров. Построение гистограмм.
2. Моделирование дискретных случайных величин методом жребия. 3. Проверка гипотез по критерию Пирсона. Корреляция и регрессия. Контроль знаний студента осуществляется по результатам выполнения контрольной работы, тестирования и заканчивается сдачей экзамена. Целью изучения дисциплины является приобретение знаний и навыков решения задач, связанных с расчетом вероятностей и числовых характеристик случайных величин и случайных событий. Задачи изучения дисциплины -правильное понимание основных положений и формул для расчета вероятностей различных событий. Иметь представление о свойствах вероятности. Знать основные определения и формулы для расчета. Уметь правильно использовать расчетную формулу для конкретно решаемой задачи. Владеть методикой расчета определения вероятности правильной работы прибора или устройства. Место дисциплины. Математика ч. 2 - в учебном процессе тесно связана с курсом Математика ч. 1, курсом Информатика и является базовой основой для различных курсов, в которых необходимо производить обработку статистических данных и делать оценки величин при выполнении дипломных проектов.
1.2. Содержание дисциплины и виды учебной работы Теория вероятностей и математическая статистика: случайные события, частота и вероятность, основные формулы для вычисления вероятностей; случайные величины, числовые характеристики дискретной и непрерывной случайных величин, нормальный закон распределении; генеральная совокупность и выборка; оценки параметров; корреляция и регрессия. Объем дисциплины и виды учебной работы
Перечень видов практических занятий и контроля: - тест (общий по дисциплине); - одна контрольная работа (для очно-заочной и заочной форм обучения); - практические занятия – 4 часа (для очной и заочной форм обучения), - 8 часов (для очно-заочной формы обучения); -лабораторные работы – 20 часов (для очной формы), 12 часов (для очно-заочной) и 10 часов (для заочной формы обучения); - экзамен.
Рабочие учебные материалы 2.1. Рабочая программа (объем 150 часов) Введение [1], с. 5; [2], с. 3-5 Теория вероятностей и математическая статистика – неразрывно связанные науки, изучающие закономерности случайных явлений. Математическая статистика – наука, которая разрабатывает методы обработки и анализа результатов наблюдений и опытов на основе теоретико-вероятностных понятий и методов для того, чтобы получить некоторые научные и практические выводы. Необходимость обрабатывать большие объемы опытных и статистических данных возникает в технике, экономике, медицине, финансах и т.д. Появляются задачи, для решения которых требуются вероятностно-статистические методы. К таким задачам можно отнести, например, задачи упорядочения результатов измерения, выборочного контроля качества, исследование надежности работы сложных систем.
Предметом изучения теории вероятностей служат случайные события и случайные величины, над которыми производятся многократные наблюдения, в результате чего делаются выводы и обобщения о числовых характеристиках, определяется закон распределения. Статистика достаточно древняя наука. Математической наукой она признана после того, как стала строиться на базе теории вероятностей. Одна из главных задач статистических методов заключается в рассмотрении выборки из генеральной совокупности, по которой производится оценка параметров, коэффициентов корреляции и регрессии. Раздел 1. Случайные события (50 часов) 1.1. Понятие случайного события (10 часов) [1], с. 6…13 Случайные события. Пространство элементарных событий. Алгебра событий. Аксиомы вероятностей и следствия из них.
1.2. Вероятности случайных событий (10 часов) [1], с. 14…22 Частота и вероятность события и свойства. Классическое определение вероятности. Геометрическое определение вероятности. Вероятность суммы событий. 1.3. Основные формулы для вычисления вероятностей. (30 часов). [1], с. 23…31 Независимость событий. Проведение независимых испытаний по схеме Бернулли. Условная вероятность. Вероятность произведения событий. Формула полной вероятности. Формула Байеса.
Раздел 2. Случайные величины (60 часов) 2.1. Описание случайных величин (20 часов) [1], с. 32…41 Определение случайной величины. Дискретные и непрерывные случайные величины. Ряд распределения и функция распределения случайной величины. Плотность вероятности случайной величины. Свойства функции распределения и плотности вероятности. 2.2. Числовые характеристики дискретной и непрерывной случайных величин (40 часов) [1], с. 59…83 Вычисление математического ожидания и дисперсии дискретной и непрерывной случайных величин. Законы распределения: биномиальный, пуассоновский, закон равномерной плотности, нормальный закон распределения (закон Гаусса). Раздел 3. Элементы математической статистики (40 часов) 3.1. Основные определения (6 час) [2], с. 6…15 Генеральная совокупность и выборка. Оценка параметров. Получение экспериментальных характеристик случайной величины. Понятие статистической гипотезы. 3.2. Систематизация выборки (14часов) [2], с.16…29 Вариационный ряд, статистическая вероятность события. Эмпирическая функция распределения, гистограмма частот. Получение опытных значений математического ожидания и дисперсии случайной величины.
3.3. Точечные оценки параметров распределения (10 час). [2], с. 24…32 Смещенная, несмещенная, состоятельная оценки параметров. Точечные оценки математического ожидания и дисперсии.
3.4. Интервальные оценки (10 часов) [3], гл.16, с.126…138 Доверительная вероятность, доверительный интервал, построение интервальных оценок, корреляция и регрессия. Основные статистические законы распределения.
Заключение. В результате изучения указанных материалов студент может выполнить задания, включенные в контрольную работу, ответить на вопросы проверочных тестов и сдать экзамен по данному курсу.
2.2. Тематический план занятий Тематический план дисциплины для студентов очной формы обучения
Тематический план дисциплины для студентов очно-заочной формы обучения
Тематический план дисциплины
для студентов заочной формы обучения
2.3. Структурно-логическая схема дисциплины
Рис. 2.1
Рис. 2.1
2.4. Временной график изучения дисциплины
(для студентов заочной формы обучения с использованием ДОТ)
2.5. Практический блок
Практические занятия (очно-заочная форма обучения)
Практические занятия (заочная формы обучения)
Практические занятия (очная форма обучения)
Лабораторные работы (очно-заочная форма обучения)
Лабораторные работы (очная форма обучения)
Лабораторные работы (заочная форма обучения)
Балльно-рейтинговая система Изучение дисциплины проводится в течение одного семестра, и состоит из усвоения 3-х теоретических разделов, выполнения 2-х лабораторных работ на ПК и одной контрольной работы. В каждом разделе приводятся вопросы тестов текущего контроля, ответы на которые не оцениваются, но являются репетицией сдачи контрольных тестов, для подготовки к которым предлагается пройти тренировочный тест, по репетиционным вопросам, приводимым в блоке 6. За каждый вид самостоятельной работы начисляется определенное число баллов: - за правильный ответ на вопрос тренировочного теста – 2 балла; - за правильно выполненную лабораторную работу – 10 баллов; - за правильно выполненную контрольную работу – 26 баллов. При успешной работе студент может получить максимум 100 баллов. Для получения допуска к экзамену нужно набрать более двух третей от этой суммы (т.е. не менее 67 баллов).
3. Информационные ресурсы дисциплины Библиографический список Основной: 1. Вентцель, Е.С. Теория вероятностей / Е.С. Вентцель. - М.: Academia, 2003. 2. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. - М.: Высш. шк., 2004. 3. Ткаченко, Г.Г. Теория вероятностей: учебное пособие / Г.Г.Ткаченко. – СПб.: Изд-во СЗТУ, 2005. 4. Шабаева, М.Б. Вычислительная математика. Элементы математической статистики / М.Б. Шабаева. – СПб.: Изд-во СЗТУ, 2004. Дополнительный: 5. Чистяков, В.П. Курс теории вероятностей / В.П. Чистяков, - СПб.: Лань, 2003. 6. Вентцель, Е.С. Теория вероятностейи ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров. - М.: Наука, 1988. 7. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. - М.: Высш. шк., 1979.
3.2. Опорный конспект по курсу “ Математика ч.2. Теория вероятностей и элементы математической статистики” ВВЕДЕНИЕ
Теория вероятностей – это математическая наука, изучающая закономерности в случайных явлениях. Случайные явления – это такие явления, которые при неоднократном воспроизведении одного и того же опыта с соблюдением некоторого комплекса условий протекают по-разному, что ведет к различным результатам опыта. Примеры случайных явлений можно наблюдать во многих областях науки и техники. Теория вероятностей основывается на построении математических моделей случайных явлений, изучении свойств моделей и применяется в задачах, которые требуют определения и расчета вероятностей отдельных испытаний или серии опытов, а также для определения надежности или устойчивости работы устройств, приборов или систем обслуживания. Настоящий «Опорный конспект» содержит теоретические основы дисциплины Математика ч. 2. Теория вероятностей и элементы математической статистики, состоит из 3-х разделов, включает варианты решения различных задач, прилагаются вопросы для самопроверки и тестовые вопросы.
Раздел 1. СЛУЧАЙНЫЕ СОБЫТИЯ
Данный раздел курса Теория вероятностей и элементы математической статистики содержит краткое изложение теоретического материала для изучения понятия случайного события, классификации событий. Кроме того, приводится классическое и геометрическое определение вероятности, сформулированы аксиомы о вероятностях и следствия из них. Рассматриваются несовместные и независимые события и приводятся формулы, по которым можно вычислить вероятность суммы и произведения различных событий, а также формула для вычисления вероятности по схеме Бернулли, формула полной вероятности и формула Байеса. Каждое понятие или приводимая формула обязательно поясняется примером, решение которого позволяет увидеть, в каких случаях следует использовать конкретную формулу, что в большой степени определяется формулировкой поставленной задачи. Изучив материал раздела, студент может проверить свои знания по вопросам для самопроверки, которые даются в конце каждой темы, а также разобрать репетиционный тест № 1, приведенный в Блоке контроля освоения дисциплины. После того, как эта часть работы проделана, студент может приступить к выполнению задачи № 1 из методических указаний по выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики [ 8 ]. Понятие случайного события Сведения из теории множеств Понятие множества относится к фундаментальным понятиям математики. Под множеством понимают некоторую совокупность объектов, называемых элементами множества. Для задания множества можно или перечислить все элементы, в него входящие, или определить свойства, которыми они обладают. Множества обозначают прописными буквами A, B, …, а их элементы – строчными буквами a, b, … и заключают в фигурные скобки. Пример 1.1. Обозначим A - множество положительных целых чисел, меньших 6 A = { 1,2,3,4,5}. Пример 1.2. Обозначим B – множество всех действительных чисел B = { x: Пример 1.3. Обозначим C множество всех жителей некоторого города, которые старше 90 лет. Если x обозначает возраст жителя этого города, то все элементы множества C можно определить C= { x: x> 90}. Выражение " элемент a принадлежит множеству A " будем символически записывать a Множества, состоящие из конечного числа элементов, называют конечными, в противном случае – бесконечными. В примерах 1.1 и 1.3 определены конечные множества, а примером бесконечного множества является множество из примера 1.2. Символом Ø будем обозначать множество, не содержащее элементов. Это множество называют пустым множеством. Например, для некоторого города множество C в примере 1. 3 может оказаться пустым. Множество B называют подмножеством множества A, если все элементы B принадлежат множеству A, и символически записывают
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.127 (0.014 с.) |



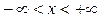 }.
}.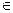 A, а запись a
A, а запись a  A будет означать " элемент a не принадлежит множеству A".
A будет означать " элемент a не принадлежит множеству A". или
или 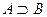 .
.


