Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы математической статистикиСодержание книги
Поиск на нашем сайте Перед тем как приступить к решению второй половины третьей задачи, следует изучить такие понятия, как: выборка, случайные числа; случайные числа распределенные по определенному закону; эмпирические (экспериментальные) ряд и функция распределения; оценки параметров распределения; метод жребия моделирования дискретной величины; критерии Пирсона оценки достоверности гипотезы; доверительные вероятности и интервалы. Следует разобрать примеры 5.10, 5.11. Коротко рассмотрим, в чем заключается метод жребия моделирования дискретной случайной величины. Пусть событие А может произойти с вероятностью р, и пусть очередное значение случайного числа – ri (случайное число – значение непрерывной случайной величины, равномерно распределенной в интервале [0,1]). Если ri £ р, то оно принадлежит интервалу Поскольку значения случайной величины ни что иное как случайные события, процедура моделирования дискретной случайной величины с заданным законом распределения аналогична моделированию случайного события. Пусть дискретная случайная величина задана теоретическим рядом распределения.
Присваиваем случайной величине h значение х 1, если значение случайного числа ri £ p (х 1), значение х 2, если p (х 1)< ri £ p (х 1)+ p (х 2), т.е. в общем случае, если Пример 5.10. Дискретная случайная величина задана рядом распределения, приведенным в табл. 5.3. Таблица 5.3
1. Построить модель этой случайной величины для партии из 25 приборов (методом жребия получить её 25 значений); найти экспериментальные ряд и функцию распределения, построить их графики. 2. Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения. 3. С помощью критерия Пирсона оценить соответствие экспериментального распределения теоретическому при уровнях значимости a1=0.01, a2= 0.05. Решение. 1. Приступим к построению модели данной случайной величины. Этот процесс будем осуществлять методом жребия с помощью случайных чисел rj, т.е. значений случайной величины равномерно распределенной в интервале Для рассматриваемой случайной величины правило моделирования заключается в том, чтобы определить какое значение будет принимать случайная величина в зависимости от попадания случайного числа в интервал. h примет значение: 0, если rj £ 0.6189, 5, если 0.6189 £ r j <0.7085, 10, если 0.7085 £ rj < 0.9631, 15, если ri >= 0.9631. Для удобства использования правило можно свести в табл. 5.4 или изобразить на рис. 5.7. Таблица 5. 4
Замечание. Поскольку в табл. 5.4 даны только 2 знака мантиссы, значения границ интервалов округлили до трех знаков после запятой. Приступая к моделированию h, возьмем первое число из табл. Д Приложения. Для того, чтобы начало было случайным, воспользуемся днем рождения решающего задачу. Допустим, он родился 9 марта. Поэтому начнем с 9-й строки 3-го столбца. Это число 67, следовательно, r 1 = 0.67, оно принадлежит второму интервалу Таблица 5.5
Найдем экспериментальный ряд распределения, для чего подсчитаем частоты mi, равные числу приборов с данной стоимостью ремонта, т.е. числу появлений значений хj, вычислим их относительные частоты, т.е. оценки вероятностей р
Таблица 5.6
Найдем экспериментальную функцию распределения F *(х)= F *(х)= Построим экспериментальные многоугольник распределения и функцию распределения (рис. 5.8). Для наглядности сравнения теоретической и экспериментальной кривых построим штриховыми линиями теоретические кривые.
Рис. 5.8 2. Найдем оценки числовых характеристик. Для вычисления оценок математического ожидания, дисперсии и среднего квадратического отклонения воспользуемся формулами:
где k – число различных значений случайной величины;
или
Поскольку формулы (5.9) и (5.10) дают смещенную оценку дисперсии, несмещенную оценку найдем по формуле
Замечание. При больших значениях n коэффициент Вычисления запишем в табл. 5.7. Таблица 5.7
Сравнив полученные результаты с теоретическими (см. пример 5.5), видим, что экспериментальные характеристики отличаются от полученных из исходного ряда распределения. Для того чтобы получить более близкие результаты, следует существенно увеличить число реализаций случайной величины (например в два раза). 3. Проверим соответствие закона распределения полученной случайной величины F * (х) заданному закону распределения F (x), используя критерий Пирсона. Для этого определяется случайная величина
где k – число значений случайной величины; mi – число появлений значений случайной величины h; pi – теоретическая вероятность значения; n – объем моделируемой выборки (npi – ожидаемое число появлений значения хi при n реализациях случайной величины). Величина c2, называемая “хи-квадрат”, служит показателем того, насколько хорошо согласуются моделируемое и ожидаемое распределения. В статистических расчетах число степеней свободы для дискретной случайной величины определяется как r = k – Введем понятие «критическое значение» C = если при проверяемой гипотезе вероятность события {χ2.> C } мала, Р (χ2.> С) = a, то С называется «критическим значением», а a – «уровнем значимости» критерия χ2. Уровень значимости является вероятностью отвергнуть правильную гипотезу. Выбор его определяется решаемой задачей. Как правило, полагают a = 0.01 или a = 0.05, т.е. в одном или пяти случаях из ста может быть отвергнута правильная гипотеза. Критические значения в зависимости от объема выборки и уровня значимости приведены в табл. С Приложения А. В рассматриваемой задаче число k = 4, поэтому число степеней свободы r = 4 - 1 = 3. По указанной таблице найдем критические числа С 1 (для a1 = 0.01) и С 2 (для a2 = 0.05): ими будут С 1 = 11,3 и С 2 = 7,8. Найдем значение χ2. Все вычисления выполним в таблице 5.8 (n = 25, значение np i вычислим с точностью до одного знака после запятой). Таблица 5.8
При уровне значимости a2 = 0.05 событие {χ2 > C 2} не произошло (5.617 < 7.8); полученное распределение не противоречит предполагаемому. При менее жестких требованиях, т.е. при a = 0.01, событие { χ2> C 1} тем более не произошло, и в этом случае можно считать, что гипотеза о распределении случайной величины с заданным законом распределения не противоречит смоделированным значениям случайной величины. Пример 5.11. Из выборки в 15 элементов нормальной генеральной совокупности найдены оценки математического ожидания Определить эти же величины для выборки в 40 элементов, если оценки оказались такими же. Решение. Истинные математическое ожидание m и дисперсия где I b – доверительный интервал, соответствующий доверительной вероятности b,
=(-2.25; -0.75). Полученный результат позволяет утверждать, что с вероятностью 0.98 математическое ожидание рассматриваемой случайной величины принадлежит интервалу (-2.25;-0.75). При выборке 40 элементов в связи с тем, что с увеличением числа степеней свободы распределение Стьюдента быстро приближается к нормальному, воспользуемся формулами e = (m *- В этих формулах z b находится как корень уравнения Ф(z b) = Вычислив Таким образом, точность оценки e= Заметим, что увеличение объема выборки существенно сузило доверительный интервал. БЛОК КОНТРОЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ Репетиционные вопросы Тест № 1 Вопрос 1 Два события называются несовместными, если … А) появление одного из них исключает появление другого; B) появление одного из них не влияет на вероятность появления другого; C) появление одного из них заключается в непоявлении другого. Вопрос 2 Два события называются независимыми, если … А) появление одного из них исключает появление другого; B) появление одного из них не влияет на вероятность появления другого; C) появление одного из них заключается в непоявлении другого. Вопрос 3 Два события называются противоположными, если … А) появление одного из них исключает появление другого; B) появление одного из них не влияет на вероятность появления другого; C) появление одного из них заключается в непоявлении другого. Вопрос 4 Событие A называется частью события B, если … А) появление события A влечет появление события B; В) появление события B влечет появление события A; С) появление события A влечет появление события B, а появление события B влечет появление события A.
Вопрос 5 Если появление одного события не влияет на вероятность появления другого события, то события называются … А) несовместными; B) независимыми; C) противоположными.
Вопрос 6 Формула P(A+B)= P(A)+P(B) применима в том случае, если события A и B … A) несовместны; B) независимы; C) совместны; D) зависимы. Вопрос 7 Формула P(A+B)= P(A)+P(B)- P(AB) применима … A) только для несовместных событий; B) для любых событий; C) только для совместных. Вопрос 8 Формула P(AB)= P(A)P(B/A) применима... A) только для независимых событий; B) только для зависимых событий; C) для любых событий.
Вопрос 9 Стрелок стреляет по мишени три раза. Пусть событие A – стрелок промахнулся. Укажите, какое из приведенных событий противоположно событию A. А) только одно попадание; В) два попадания; С) три попадания; Д) хотя бы одно попадание. Вопрос 10 Игральный кубик бросается два раза. Укажите, какое из приведенных событий является эквивалентным событию: выпало максимальное число очков. A) выпало более одного очка; B) выпало более шести очков; C) выпало более одиннадцати очков; D) выпало менее одиннадцати очков. Вопрос 11 В урне два белых и три красных шара. Наудачу извлекается 3 шара. Укажите, какое из событий является противоположным событию: извлечены три красных шара. A) извлечены три белых шара; В) извлечен хотя бы один белый шар; С) извлечены два белых и один красный шар; D) извлечены один белый и два красных шара. Вопрос 12 Стрелок стреляет по мишени два раза с вероятностью попадания при каждом выстреле 0.6. Найти вероятность того, что оба раза мишень будет поражена. A) 0.36; B) 0.76; C) 0.16; D) 0.84. Вопрос 13 В одной урне 6 белых и 4 цветных шара, в другой – 4 белых и четыре цветных. Из наугад взятой урны наугад выбирается один шар. Найти вероятность того, что он будет белым. А) 0.90; B) 0.45; C) 5/9@0.56; D) 0.55.
Вопрос 14 Cобытие А = {переменная X принадлежит промежутку (- ∞, а)} Событие В = { переменная X принадлежит промежутку (b, + ∞)}.
Событие А + В = … А) {переменная X принадлежит промежутку (- ∞, + ∞)}; B) {переменная X принадлежит промежутку (b, a)}; C) {переменная X принадлежит промежутку (a, ¥)}; D) {переменная X принадлежит промежутку (- ∞, a). Вопрос 15 Подбрасываются две различные монеты. Пространство элементарных событий: W={ГГ,ГЦ,ЦГ,ЦЦ}. Множество элементов пространства элементарных событий, благоприятствующих событию A={на первой монете появился герб} … A) { ГГ, ГЦ}; B) {ГГ, ЦЦ}; C) { ГГ, ЦГ}; D) {ГЦ, ЦГ}. Вопрос 16 В цехе 4 станка. Вероятность того, что каждый из станков работает в данный момент, равна 0,9. Найти с точностью до сотых вероятность того, что в данный момент включены все станки. А) 0,66;B) 0,5; C) 1; D) 0,81. Вопрос 17 Cобытие А = {переменная X принадлежит промежутку (- ∞, а)}. Cобытие В = { переменная X принадлежит промежутку (b, + ∞)}.
Событие АВ = … А) {переменная X принадлежит промежутку (b, a)}; B) {переменная X принадлежит промежутку (- ∞, + ∞)}; C) {переменная X принадлежит промежутку (a, ¥)}; D) {переменная X принадлежит промежутку (- ∞, a). Вопрос 18 В группе 20 человек. На студенческую конференцию надо выбрать двух человек. Сколькими способами это можно сделать? A) 380; B) 190; C) 15; D) 400. Вопрос 19 Подбрасываются две различные монеты. Пространство элементарных событий: W={ГГ,ГЦ,ЦГ,ЦЦ}. Множество элементов пространства элементарных событий, благоприятствующих событию A = {на первой монете появился герб} … A) {ГГ, ГЦ};B) {ГГ, ЦЦ}; C) {ГГ, ЦГ}; D) {ГЦ, ЦГ}. Вопрос 20 Для участия в олимпиаде выделено из первой группы 5 студентов, из второй – 2 студента, из третьей – 3 студента. Вероятность того, что студент станет участником олимпиады для первой группы равна 0,9, для второй – 0,7, для третьей – 0,8. Найти вероятность того, что наудачу выбранный студент попал на олимпиаду. A) 0,83; B) 0,35; C) 0,24; D) 0,29 Тест № 2 Вопрос 1 Случайная величина задана рядом распределения:
Математическое ожидание этой случайной величины равно 0. Найти её дисперсию. А) 4,8; B) 5,4; C) 1; D) 2,4. Вопрос 2 Случайная величина задана плотностью вероятности
Найти математическое ожидание этой случайной величины. А) 3; B) 4/3; C) 2/ Вопрос 3 Случайная величина задана плотностью вероятности
Найти дисперсию данной случайной величины. А) 4/3; B) 1.3; C) 2/ Вопрос 4 Дана плотность вероятности случайной величиныη, распределенной по нормальному закону.
Математическое ожидание и дисперсия этой случайной величины равны … А) M[h] = -7; D[h] = 3; B) M[h] = 7; D[h] = 3; C) M[h] = -7; D[h] = 9; D)M[h] = 7; D[h] = 9. Вопрос 5 Случайная величина задана функцией распределения
Найти вероятность того, что случайная величина примет положительные значения. A) 0,8413 B) 0,1587; C) 0,3413; D) 0,5; Вопрос 6 Дан график плотности вероятности f(x) случайной величины, равномерно распределенной на интервале [- 2, 4]. f(x)
- 2 0 4 Математическое ожидание и дисперсия этой случайной величины равны соответственно … А) M[h] = 1; D[h] = 3; B) M[h]=2; D[h]=3; C) M[h]=1; D[h]=9; D. M[h]=2; D[h]=9. Вопрос 7 Случайная величина задана рядом распределения:
Найти вероятность того, что случайная величина будет принимать положительные значения. А) 0,2; B) 0,4; C) 0,6; D) 0,8.
Таблица ответов к тесту №1
Таблица ответов к тесту №2
Вопросы для экзамена по курсу «Математика ч.2. Теория вероятностей и элементы математической статистики» 1. Пространство элементарных событий. 2. Сумма, произведение, разность событий. Несовместные события. 3. Относительные частоты событий, закон устойчивости относительных частот. 4. Аксиомы теории вероятностей. 5. Противоположные события. Вероятность суммы событий. 6. Элементы комбинаторики (размещения, сочетания из n элементов по k элементов). 7. Классическое определение вероятности, примеры. 8. Гипергеометрическое распределение. 9. Геометрическое определение вероятности, примеры. 10. Условная вероятность, примеры. 11. Теорема умножения вероятностей для нескольких событий. 12. Попарно независимые события. Привести примеры. 13. Независимые события в совокупности. 14. Формула полной вероятности. 15. Формула Байеса. 16. Последовательность независимых испытаний (схема Бернулли). 17. Дискретная случайная величина и ряд распределения. 18. Функция распределения и ее свойства. 19. Плотность вероятности распределения случайной величины. 20. Плотность вероятности равномерного распределения. 21. Математическое ожидание случайной величины. 22. Дисперсия случайной величины. 23. Математическое ожидание и дисперсия равномерно распределенной случайной величины. 24. Биномиальный закон распределения. 25. Нормальное распределение случайной величины и его свойства. 26. Закон больших чисел, центральная предельная теорема. 27. Генеральная совокупность, числовые характеристики генеральной совокупности. 28. Выборка, выборочное среднее. 29. Состоятельные и несмещенные оценки (дисперсия, стандартное отклонение). 30. Интервальный вариационный ряд, гистограмма. 31. Доверительный интервал для математического ожидания при известной дисперсии (большая выборка). 32. Доверительный интервал для математического ожидания при неизвестной дисперсии (малая выборка). 33. Проверка гипотез по критерию Пирсона.
Продолжение таблицы В
Окончание таблицы В
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

 , поэтому считаем, что событие А наступило. Если ri > р, то считается, что событие А не наступило.
, поэтому считаем, что событие А наступило. Если ri > р, то считается, что событие А не наступило. , то случайной величине h присваивается значение хm .
, то случайной величине h присваивается значение хm . . Эти значения приведены в табл.Д Приложения. Моделируемые значения случайной величины обозначим Zj (j = 1, 2, …, 25). Заметим, что каждое из них следует рассматривать как случайную величину.
. Эти значения приведены в табл.Д Приложения. Моделируемые значения случайной величины обозначим Zj (j = 1, 2, …, 25). Заметим, что каждое из них следует рассматривать как случайную величину.

 , поэтому х 1 = 5. Таким образом, найдена стоимость ремонта первого прибора. Аналогично моделируются стоимости остальных приборов. Далее случайные числа будем выбирать двигаясь, например, по строкам влево или вправо. Второе число 43, т.е. r 2 = 0.43, оно из интервала
, поэтому х 1 = 5. Таким образом, найдена стоимость ремонта первого прибора. Аналогично моделируются стоимости остальных приборов. Далее случайные числа будем выбирать двигаясь, например, по строкам влево или вправо. Второе число 43, т.е. r 2 = 0.43, оно из интервала  , поэтому х 2=0. Сведем процесс нахождения реализаций h в табл. 5.5.
, поэтому х 2=0. Сведем процесс нахождения реализаций h в табл. 5.5. =
=  , и занесем результаты в табл. 5.6.
, и занесем результаты в табл. 5.6.
 :
: .
.
 , (5.8)
, (5.8) (5.9)
(5.9) . (5.10)
. (5.10) . (5.11)
. (5.11) очень близок к единице, и можно считать оценку, вычисленную по формулам (5.9) или (5.10), оценкой несмещенной дисперсии.
очень близок к единице, и можно считать оценку, вычисленную по формулам (5.9) или (5.10), оценкой несмещенной дисперсии.



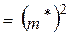
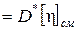
 ,
, .
.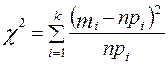 ,
, - 1, где k – число значений слу-чайной величины,
- 1, где k – число значений слу-чайной величины,  следующим образом:
следующим образом: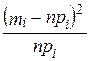
 = -1.5 и несмещенной дисперсии s 2= 1.21. Найти точность оценки математического ожидания и доверительный интервал, соответствующие доверительной вероятности b = 0.98.
= -1.5 и несмещенной дисперсии s 2= 1.21. Найти точность оценки математического ожидания и доверительный интервал, соответствующие доверительной вероятности b = 0.98. 2 данного нормального распределения не известны, поэтому воспользуемся формулами
2 данного нормального распределения не известны, поэтому воспользуемся формулами  и
и  ,
,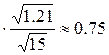 и доверительный интервал I 0.98 =(-1.5-0.75;-1.5+0.75) =
и доверительный интервал I 0.98 =(-1.5-0.75;-1.5+0.75) = zb для вычисления предельной ошибки оценки математического ожидания и I b = (m * - e; m * + e) =
zb для вычисления предельной ошибки оценки математического ожидания и I b = (m * - e; m * + e) = z b; m*+
z b; m*+  по таблице значений нормированной функции распределения нормального закона (табл. В Приложения). z b называется квантилью порядка
по таблице значений нормированной функции распределения нормального закона (табл. В Приложения). z b называется квантилью порядка  = 0.99, входим с этим значением функции в табл.В Приложения и находим её аргумент, равный 2,327.
= 0.99, входим с этим значением функции в табл.В Приложения и находим её аргумент, равный 2,327. , а доверительный интервал I 0.98 = (-1.5–0.405; -1.5+0.405) = (-1.905; -1.045).
, а доверительный интервал I 0.98 = (-1.5–0.405; -1.5+0.405) = (-1.905; -1.045). - ∞ b а + ∞
- ∞ b а + ∞
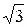 ; D) 0.25.
; D) 0.25.