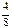Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретные случайные величиныСодержание книги
Поиск на нашем сайте
Определение. Случайную величину x называют дискретной, если множество ее возможных значений образует конечную или бесконечную последовательность чисел, т.е. конечно или счетно. Пусть возможные значения дискретной случайной величины xупорядочены по возрастанию x 1 ≤ x 2 ≤¼≤ x n ≤¼.. Рассмотрим события Ai, содержащие все элементарные события w, приводящие к значению xi: A i= {w: x = x i }, i= 1, 2, ¼ Пусть pi обозначает вероятность события Ai: pi = R (Ai) =R (w: x = xi ), i= 1, 2, ¼. События Ai - несовместные события, которые составляют разбиение пространства элементарных событий Ω, т.е. Ω = Тогда для вероятностей pi выполняются свойства p i ³ 0, i= 1, 2, ¼ Закон распределения дискретной случайной величинызадается рядом распределения. Ряд распределения дискретной случайной величины x может быть представлен таблицей, в первой строке которой помещают возможные значения xi, а во второй - вероятности pi, соответствующие этим значениям.
Кроме ряда распределения, дискретная случайная величина может быть задана с помощью функции распределения. Определение. Функция распределения F(x) случайной величины x это такая функция переменной x, которая равна вероятности того, что случайная величина примет значение, меньшее, чем заданное x, F (x) =P (w: ¦ (w) £ x) (2.3) для всех действительных чисел x. Для дискретной случайной величины функция распределения определяется как сумма вероятностей для тех значений случайной величины, которые меньше заданного x. Обозначим через В (x) множество возможных значений случайной величины x, предшествующих числу x: B (x) = { xi: xi £ x }. (2.4) Тогда формулу(2.3) можно записать в виде F (x) = Приведем несколько примеров функций распределения дискретных случайных величин. Пример 2.3. Правильный кубик подбрасывают один раз, и величина x обозначает число очков, выпавшее на его верхней грани. Построим функцию распределения этой случайной величины. Решение. Обозначим через X возможные значения случайной величины x. В данном примере X ={1,2,3,4,5,6}, и вероятность появления грани с любым количеством очков равна рi = Напишем ряд распределения этой дискретной случайной величины.
Построим функцию распределения по формуле (2.5). Для этого на числовой оси отметим точки из множества X. Они разбивают числовую ось O x на интервалы (-∞,1), [1,2) [2,3) [3,4) [4,5) [5,6) [6,+ ∞). Последовательно будем вычислять функцию распределения на каждом из указанных выше интервалов. При любом F(x)= При любом В(x)={ xi: xi £ x }={1}. Тогда по формуле (2.5) F(x)= При любом F (x) = При любом F (x) = При любом F (x) = При любом F (x) = При любом F (x) = Заметим, что при переходе от одного интервала к другому множество B (x) расширяется на одно значение и от пустого множества переходит к множеству всех возможных значений X ={1,2,3,4,5,6}. Все вычисления можно объединить в формулу
Пример 2.4. Построим функцию распределения для появления числа гербов при трех подбрасываниях монеты (пример 2.1). Решение. Ряд распределения был найден в примере 2.1.
Обозначим через X множество всех возможных значений этой случайной величины X = { 0, 1, 2, 3 }. Заметим, что множество B (x) при любом x является подмножеством X. Числа из множества X разбивают числовую ось на интервалы (-¥,0), [0,1), [1,2), [2,3), [3,+¥). Пусть x любое число из интервала (-¥, 0). Тогда множество B (x) не содержит значений случайной величины x, т.е. B (x) = Ø, следовательно, F (x)=0 при всех x из (-¥,0). Возьмем любое x Î[0,1). Множество B (x) содержит значение 0: B (x) ={0} и F (x) = p 0 = Возьмем x Î[1,2). Множество B (x) ={0,1}, и F (x) = p 0+ p 1= Для всех x Î[2,3) множество B (x) ={0,1,2}, и F (x)= p 0+ p 1+ p 2= Для всех x Î[3,¥) множество B (x)={0,1,2,3}= X. Отсюда следует F (x) = p 0+ p 1+ p 2+ p 3= Запишем полученные значения функции распределения на отдельных интервалах в виде формулы
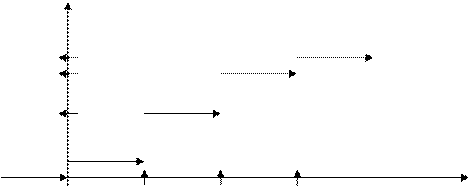
Построим график функции распределения F (x) дискретной случайной величины
0 1 2 3 x
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.006 с.) |

 Ai.
Ai.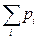 = 1. (2.2)
= 1. (2.2)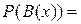
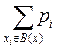 . (2.5)
. (2.5)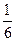 .
.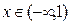 множество B (x)={ xi: xi £ x } не содержит возможных значений случайной величины, т.е. является пустым множеством. Тогда по формуле (2.5)
множество B (x)={ xi: xi £ x } не содержит возможных значений случайной величины, т.е. является пустым множеством. Тогда по формуле (2.5)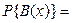 0.
0.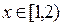 множество будет состоять из одного значения - 1:
множество будет состоять из одного значения - 1: p1 =
p1 = 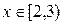 множество B (x)={ xi: xi £ x }={1,2}. Тогда по формуле
множество B (x)={ xi: xi £ x }={1,2}. Тогда по формуле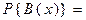 p1+ p2=
p1+ p2=  .
. множество B (x) = { xi: xi £ x }={1,2,3}. Тогда
множество B (x) = { xi: xi £ x }={1,2,3}. Тогда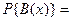 p1+ p2+ p3=
p1+ p2+ p3= 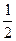 .
.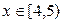 множество B (x)={ xi: xi £ x }={1,2,3,4}. Тогда
множество B (x)={ xi: xi £ x }={1,2,3,4}. Тогда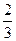 .
.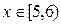 множество B (x)={ xi: xi £ x }={1,2,3,4,5}.Тогда
множество B (x)={ xi: xi £ x }={1,2,3,4,5}.Тогда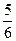 .
.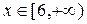 множество B (x)={ xi: xi £ x }={1,2,3,4,5,6} = X. Тогда
множество B (x)={ xi: xi £ x }={1,2,3,4,5,6} = X. Тогда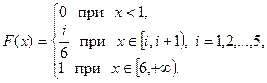 . (2.6)
. (2.6)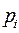
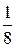
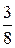
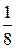 .
.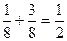 .
. .
. .
.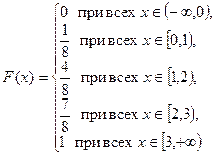 .
. F(x)
F(x)