
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности и формула БайесаСодержание книги
Поиск на нашем сайте
Теорема. Пусть A - некоторое событие, и события H 1, H 2, ¼, Hn, , попарно несовместные, т.е. Hi Hj=Æ, i ¹ j, образующие полную группу, и появление одного из них и только одного есть событие достоверное. Допустим, что событие A может произойти вместе с одним из событий Hi Тогда имеет место формула полной вероятности p (A) = и формула Байеса p (Hi | A)=
Замечание. События Hi называют гипотезами, вероятности p (Hi) - априорными вероятностями гипотез Hi, а вероятности p (Hi|A) - апостериорными вероятностями гипотез Hi. Пример 1.19. В первой урне находится 4 белых и 6 черных шаров, а во второй – 2 белых и 7 черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны наудачу извлекают один шар. 1) Найти вероятность, что шар, извлеченный из второй урны, белый. 2) Известно, что из второй урны извлечен белый шар. Найти вероятность того, что из первой урны во вторую был переложен черный шар. Решение. Обозначим события H1 = {из первой урны во вторую был переложен белый шар}, H2 = {из первой урны во вторую был переложен черный шар}, A = {шар, извлеченный из второй урны, белый}.
а) По классическому определению вероятности находим вероятности гипотез H 1и H 2: p (H 1) - вероятность того, что из всех находящихся в первой урне шаров во вторую был переложен белый шар - p (H 1) = 4 / 10 = 0,4, p (H 2) - - вероятность того, что из всех находящихся в первой урне шаров во вторую был переложен черный шар - p (H 2) = 6/ 10 = 0,6, и условные вероятности: p (A/H 1) – вероятность того, что из второй урны будет вынут белый шар, при условии, что в нее был переложен белый шар - p (A/H 1) = 3/10 = 0,3. p (A/H 2) - вероятность того, что из второй урны будет вынут белый шар, при условии, что в нее был переложен черный шар - p (A/H 2) = 2/10 = 0,2. Тогда по формуле полной вероятности находим вероятность искомого события A p (A) = p (H 1) p (A/H 1) +p (A/H 2) p (H 2) = 0,4×0,3 +0,6×0,2 = 0,24. б) Во второй части задачи требуется найти условную вероятность p (H 2/ A). Для этого можно использовать формулу Байеса (1.11):
p (H 2/ A) = Вопросы для самопроверки 1. Какие условия должны быть выполнены для проведения опытов по схеме Бернулли? 2. По какой формуле вычисляется условная вероятность? 3. Как вычисляется вероятность произведения: а) для независимых событий? б) для несовместных событий? в) для любых других типов событий? 4. В чем смысл формулы полной вероятности?
В результате изучения материала раздела 1 студент может выполнить задание № 1 из методических указаний по выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики ([ 8 ]). Раздел 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ В этом разделе содержится материал о случайных величинах: дискретных и непрерывных. Приводятся определения и описываются способы задания случайных величин с помощью ряда распределения и функции распределения. Способы определения плотности вероятности зависят от того, какое распределение имеет случайная величина. Рассматривается решение задач, в которых необходимо вычислить числовые характеристики случайных величин, а также написать выражение для плотности вероятности случайной величины, если она имеет биномиальное распределение, равномерное распределение или нормальное распределение. Изучение материала раздела заканчивается ответами на вопросы для самопроверки и рассмотрением репетиционного теста №2, приведенного в Блоке контроля и освоения дисциплины. После того, как эта часть работы проделана, студент может приступить к выполнению задачи № 2 из Методических указаний по выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики [ 8 ].
Описание случайных величин 2.1.1. Определение и способы задания случайной величины Одним из основных понятий теории вероятности является понятие случайной величины. Рассмотрим некоторые примеры случайных величин: 1) число попаданий в цель при трех выстрелах. Возможные результаты таковы: 0,1,2 или 3 раза попадания. 2) число вызовов, поступивших на телефонную станцию за сутки. Значениями может быть любое число от 1, 2, 3,…. Случайной величиной называется такая величина, которая в результате опыта может принимать различные значения, причем заранее неизвестно, какое именно, и известны вероятности, с которыми случайная величина принимает каждое конкретное значение. Определение. Любое соотношение, устанавливающее связь между всеми возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины. Чтобы задать случайную величину, надо указать ее закон распределения. Случайные величины принято обозначать греческими буквами x, h, q, а их возможные значения – латинскими буквами с индексами xi, yi, zi. Пример 2.1. Обозначим буквой x число гербов, выпавших при подбрасывании монеты три раза. Это число зависит от случайных результатов подбрасывания и поэтому будет случайной величиной. В этом примере случайная величина x может принять четыре значения 0,1,2,3, но невозможно предсказать какое из них. Найдем вероятности этих значений. Пространство элементарных событий
где Г обозначает выпадение герба при одном подбрасывании, а Ц – выпадение цифры. Обозначим через Аi событие, в котором при подбрасывании монеты появились i гербов (i= 0,1,2,3). Каждое событие Аi является составным событием и содержитвсе элементарные события ωi ,которые привели к появлению i гербов: Аi= { Следовательно, A 0 = { A 2 = { Дополнительно предположим, что подбрасывают правильную монету. Тогда из независимости испытаний следует, что вероятность каждого элементарного события ω i равна p 0 =P (A 0) = P{ЦЦЦ }= p 2 =P (A 2) =P { ГГЦ,ГЦГ,ЦГГ } = Отметим, что все события Ai несовместны и составляют пространство элементарных несовместных событий W = A 0 +A 1 +A 2 +A 3. Из аксиом вероятности следует равенство р( W) = р(A 0 +A 1 +A 2 +A 3) = p (A 0) + p (A 1) + p (A 2) + p (A 3) = 1. Составим таблицу из полученных возможных значений этой случайной величины и соответствующих вероятностей:
Пример 2.2. Производится один выстрел по плоской круглой мишени радиуса R. Учитываются только выстрелы, которые приводят к попаданию в мишень. В качестве случайной величины рассмотрим расстояние x от точки попадания до центра мишени. Тогда множество возможных значений случайной величины образует числовой интервал [0, R ]. Предположим, что любая точка мишени может быть поражена с одинаковой вероятностью. Отсюда следует, что с одинаковой вероятностью случайная величина x принимает любое значение из интервала [0, R ]. В этом случае вероятность того, что расстояние x не превзойдет числа x (0≤ x ≤ R), можно найти из геометрического определения вероятности по формуле R (x £ x) = x/R. Очевидно, что при x>R вероятность R (x £ x)=1, а при x <0 вероятность R (x £ x)=0. Из приведенных примеров видно, что случайной величиной являетсяфункция f, которая каждому элементарному событию w ставит в соответствие число ¦ (w). Эти числа ¦ (w) называют возможными значениями случайной величины. В зависимости от множества возможных значений случайной величины выделяют два типа случайных величин: а) дискретная случайная величина – это величина, значения которой можно (пересчитать) перенумеровать; б) непрерывная случайная величина – это такая величина, значения которой заполняют целиком некоторый промежуток числовой оси или всю числовую ось. Определение. Функция распределения F(x) случайной величины x определяется равенством F (x) =P (w: ¦ (w) £ x), (2.1) для всех действительных чисел x. В примере 2.2функция распределения определяется формулой
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.01 с.) |

 p (A | Hi)(1.10)
p (A | Hi)(1.10)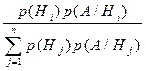 . (1.11)
. (1.11) .
. в этом примере состоит из восьми упорядоченных троек
в этом примере состоит из восьми упорядоченных троек }.
}. } = { ЦЦЦ }, A 1={
} = { ЦЦЦ }, A 1={  }={ ГЦЦ, ЦГЦ, ЦЦГ },
}={ ГЦЦ, ЦГЦ, ЦЦГ },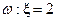 }={ ГГЦ, ГЦГ, ЦГГ }, A 3={
}={ ГГЦ, ГЦГ, ЦГГ }, A 3={  }={ ЦЦЦ }.
}={ ЦЦЦ }. *
*  . Из классического определения вероятности события Ai имеют вероятности, равные
. Из классического определения вероятности события Ai имеют вероятности, равные , p 1 =P (A 1) =P { ГЦЦ,ЦГЦ, ЦЦГ } =
, p 1 =P (A 1) =P { ГЦЦ,ЦГЦ, ЦЦГ } =  ,
, , p 3 =P (A 3) =P { ЦЦЦ } =
, p 3 =P (A 3) =P { ЦЦЦ } =  .
. , т.е.
, т.е.




 .
.


