
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функций, непрерывных на множествеСодержание книги
Поиск на нашем сайте Теорема 1. Сумма и произведение конечного числанепрерывных на некотором множестве функций есть функция, непрерывная на этом множестве. Доказательство (следует из основных теорем о пределах). Пусть f(x) и g(x) – непрерывны в точке х 0, тогда Следовательно, функция y=f(x)+g(x) непрерывна в точке х 0. Доказательство для произведения функций проводится аналогично. Теорема 2. Частное от деления двух непрерывных на множестве функций есть функция, непрерывная во всех точках, в которых знаменатель отличен от нуля. Теорема 3 (теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве функция достигает на нем своего наибольшего и наименьшего значений.
Точки разрыва функции Функция является непрерывной в точке, если Определение 1. Точки, в которых нарушается условие непрерывности, называют точками разрыва функции. Определение 2. Точка разрыва х 0 называется точкой разрыва первого рода, если существуют конечные односторонние пределыв этой точке. Определение 3. Точка разрыва первого рода называется точкой устранимого разрыва, если односторонние пределы в этой точке равны. Определение 4. Скачком функции в точке разрыва первого рода называется модуль разности односторонних пределов в этой точке. Определение 5. Точка х 0 называется точкой разрыва второго рода, если она не является точкой разрыва первого рода (если хотя бы один из односторонних пределов не существует или равен +¥(-¥)). Пример 1. х =3 – точка устранимого разрыва. Функцию можно доопределить до непрерывной функции:
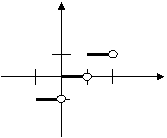
Пример 2. y =[ x ] – целая часть числа. Рассмотрим точку х =1. Следовательно, х =1 – точка разрыва первого рода, скачок в ней равен единице.
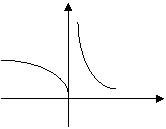
Пример 3. Рассмотрим функцию Следовательно, х =0 – точка разрыва второго рода.
Производная
Пусть функция у=f(x) определена и непрерывна на (a,b), пусть Определение 1. Производной функции в данной точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует и конечен. Функция называется дифференцируемой в точке х 0. Определение 2. Функция называется дифференцируемой на множестве А Ì R, если она дифференцируема в каждой точке множества А.
Геометрический смысл производной
Пусть функция у=f(x) определена и непрерывна на (a,b), Проведем секущую к графику через точки А (х 0, f(x 0 )), В (x 0 +Dx, f(x 0 +Dx)).
Рассмотрим DABC. При секущая стремится к касательной, Переходя к пределу при
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в данной точке. Связь между непрерывностью И дифференцируемостью функции
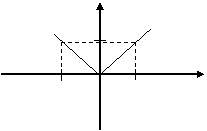
Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то онанепрерывна в этой точке. Доказательство. Пусть функция у=f(x) дифференцируема в точке х 0. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу. Найдем Следовательно, у=f(x) непрерывна в точке х 0. Следствие. Если х 0 – точка разрыва функции, то в ней функция не дифференцируема. Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость. Пример. у=|х|, х 0 = 0.
х> 0, Dх< 0, В точке х 0 = 0функция непрерывна, но производной не существует.
Свойства производных
Теорема 1. Производная постоянной функции равна нулю. Доказательство. f(x)=c,"x 0 Dy=f(x 0 +Dx) - f(x 0 )=c-c=0, Теорема 2. Если функции u, v, w дифференцируемы в некоторой точке, то и их алгебраическая сумма также дифференцируема в этой точке, причем производная алгебраической суммы равна алгебраической сумме производных и выполняется равенство Теорема 3. Если функции u и v дифференцируемы в некоторой точке, то и их произведение также дифференцируемо в этой точке, причем выполняется равенство Следствие. Постоянный множитель можно выносить за знак производной. Теорема 4. Если функции u и v дифференцируемы в некоторой точке и функция v в этой точке отлична от нуля, то существует производная частного в этой точке, причем Теорема 5 (производная сложной функции). Если функции y=f(z) и Теорема 6 (теорема Лагранжа). Конечное приращениедифференцируемой функции равно произведению соответствующего приращения аргумента на производную функции в некоторой промежуточной точке. Теорема 7 (теорема Ролля). Между двумя нулями дифференцируемой функции всегда найдется хотя бы один ноль производной. Доказательство. Пусть f(x 1 )=f(x 2 )= 0. Из теоремы Лагранжа следует, что найдется точка с, Две последние теоремы носят название теорем о конечных приращениях.
Дифференциал
Определение. Главная линейная относительно D х часть малого приращения функции называется дифференциалом функции и обозначается dy. Если малое приращение функции можно представить в виде Пример. Теорема. Функция не может иметь двух различных дифференциалов. Доказательство. Предположим противное – функция имеет два дифференциала. Тогда малое приращение функции можно представить в виде где Разделим обе части на D х: Переходя к пределу в обеих частях равенства при Полученное противоречие доказывает теорему. Связь между производной и дифференциалом Теорема 1. Если функция дифференцируема в некоторой точке, то в этой точке она имеет дифференциал. Доказательство. Функция По теореме о связи предела и б.м. функции: где Умножим обе части на D х: Следовательно, функция имеет дифференциал и Теорема 2. Если функция имеет дифференциал в некоторой точке, то она имеет производную в этой точке. Доказательство. Пусть функция имеет дифференциал Разделим обе части на D х: Переходя к пределу при Таким образом, функция имеет производную и Из этих теорем следует, что Дифференциал независимой переменной
Рассмотрим функцию у=х, dy=dx. Из теорем о связипроизводной и дифференциала следует, что: dy =1 · D x, dx = dy =D x. Дифференциал независимой переменной равен маломуприращению этой переменной. Таким образом, получена формула для вычисления дифференциала функции: Дифференциал функции равен произведению производной функции в данной точке на дифференциал независимой переменной.
|
||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

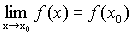 ,
, 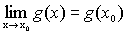 ,
,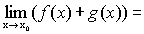
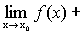
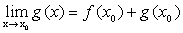 .
.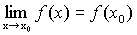 ó
ó 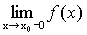 =
= 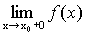
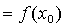 .
.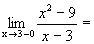 ,
,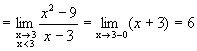
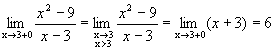 ,
,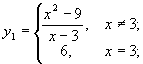 ó y=x+ 3 - непрерывная функция.
ó y=x+ 3 - непрерывная функция.
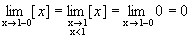 ,
, .
.
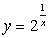 в точке х =0.
в точке х =0.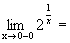
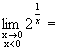 0,
0, 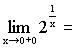
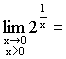 +¥,
+¥,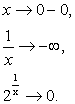
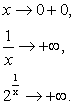
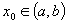 . Дадим в точке х 0 приращение аргументу Dх так, что точка х 0+ Dх
. Дадим в точке х 0 приращение аргументу Dх так, что точка х 0+ Dх 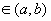 . Тогда функция получит соответствующее приращение Dу=f(x 0 +Dx)-f(x 0 ).
. Тогда функция получит соответствующее приращение Dу=f(x 0 +Dx)-f(x 0 ).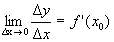 .
. Определение 1. Касательной к плоской кривой называется предельное положение секущей, когда вторая точка пересечения неограниченно приближается по кривой к первой точке.
Определение 1. Касательной к плоской кривой называется предельное положение секущей, когда вторая точка пересечения неограниченно приближается по кривой к первой точке.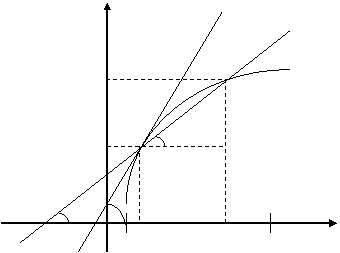
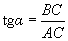 ,
, 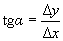 .
.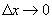
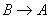 ,
,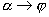 ,
,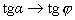 ,
,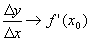 .
.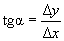 , получим
, получим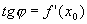 .
.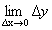 .
.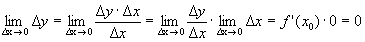 .
.
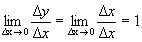 ;
;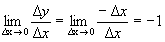 .
.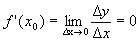 .
.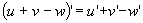 .
.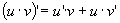 .
.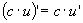 .
.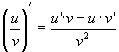 .
.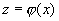 - дифференцируемые функции своих аргументов, то и их композиция является дифференцируемой функцией, причем производная сложной функции равна производной внешней функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной.
- дифференцируемые функции своих аргументов, то и их композиция является дифференцируемой функцией, причем производная сложной функции равна производной внешней функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной.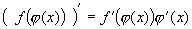 .
.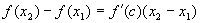 .
.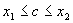 , такая, что
, такая, что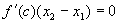 =>
=> 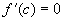 .
.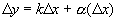 , где
, где 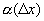 - б.м. функция более высокого порядка, чем D х при
- б.м. функция более высокого порядка, чем D х при 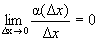 ), тогда
), тогда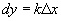 .
.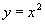 .
.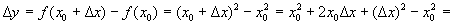
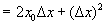 ,
,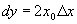 .
.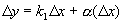 ,
,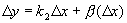 ,
,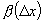 - б.м. функции более высокого порядка, чем D х при
- б.м. функции более высокого порядка, чем D х при 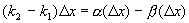 .
.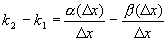 .
.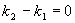 ,
,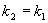 .
.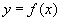 - дифференцируема в точке х 0,
- дифференцируема в точке х 0,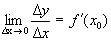 .
.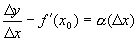 ,
,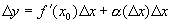 ,
,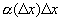 - б.м. функция более высокого порядка, чем Dх.
- б.м. функция более высокого порядка, чем Dх.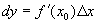 .
.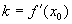 .
.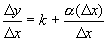 .
.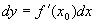 .
.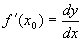 .
.


