
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первообразная. Неопределенный интегралСодержание книги
Поиск на нашем сайте
Определение 1. Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции. (F (x))' = f (x). Теорема 1 (теорема Коши). Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную. Пример. Функция F(x)=x 3 является первообразной функции f(x)= 3 x 2 так как (x 3 )'= 3 x 2. Функции F 1 (x)=x 3 + 3 и F 2 (x)=x 3 - 2 также являются первообразными функции f(x). Любая функция вида F(x)=x 3 +с, где с – произвольное число, является первообразной функции f(x). Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое. Верно и обратное утверждение. Теорема 2. Если F 1 (x) и F 2 (x) - две первообразные для функции f(x), то они отличаются на постоянное слагаемое. Доказательство. Рассмотрим функцию Ф(х) = F 1 (x) - F 2 (x). Ф'(х) = F 1 '(x) - F 2 '(x) = f(x) - f(x) = 0, Ф(х) = C, F 1 (x) = F 2 (x) +C. Определение 2. Совокупность всех первообразных даннойнепрерывной функции называется неопределенным интегралом от этой функции и обозначается ò f(x)dx, где f(x) именуетсяподынтегральной функцией, выражение f(x)dx - подынтегральным выражением. Если F(x) - некоторая первообразная данной функции, то ò f(x)dx = F(x) + C, где C - произвольная постоянная. Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции. Первообразные имеют следующий геометрический смысл. Пусть F 1 (x) и F 2 (x) - первообразные функции y=f(x). Найдем их производные в точке х 0.
Следовательно, и сами графики будут располагаться параллельно. На основании теоремы 2 F 1 (x) и F 2 (x) отличаются на постоянное слагаемое, следовательно, один график можно получить из другого сдвигом на C единиц вдоль оси ОY. F 1(x) = F 2(x) + C.
Функция имеет бесконечно много первообразных, которые отличаются друг от друга на постоянное слагаемое. Графики всех первообразных представляют собой бесконечное семейство параллельных кривых, которые заполняют всю плоскость. Через каждую точку плоскости проходит график одной из первообразных. Свойства неопределенного интеграла
Теорема 1. Производная от неопределенного интеграларавна подынтегральной функции, дифференциал от неопределенного интеграла равен подынтегральному выражению. Доказательство. Пусть функция f(x) имеет первообразную F(x), тогда ò f(x)dx = F(x) + c. Найдем производную и дифференциал от обеих частей равенства. (ò f(x)dx) ' = (F(x) + c)' = f(x), d (ò f(x)dx) = (ò f(x)dx) ' dx = f(x)dx. Теорема 2. Интеграл от дифференциала функции равен этой функции с точностью до постоянного слагаемого. Доказательство. ò d f(x) = ò f'(x)dx = f(x) + C. Из теорем 1 и 2 следует, что операции дифференцирования и интегрированияявляются взаимнообратными. Теорема 3. Постоянный множитель можно выносить за знак интеграла. Доказательство. Пусть функция f(x) имеет первообразную F(x). ò f(x)dx = F(x) + C. Умножим обе части на k. k ò f(x)dx = k F(x) + C1, где C1 = k C . Найдем производную функции kF(x). (k F(x))' = k f(x). Функция k F(x) является первообразной функции k f(x). Следовательно, ò k f(x)dx = k F(x) + C, ò k f(x)dx = k ò f(x)dx. Теорема 4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.
Непосредственное интегрирование
Этот вид интегрирования состоит в приведении исходного интеграла к одному или к нескольким табличным с помощью свойств интеграла и тождественных преобразований. Пример 1. Пример 2. Метод замены переменной В неопределенном интеграле
Теорема 1. Пусть функция х = φ (t) определена идифференцируема на некотором промежутке Т, а Х – множество значений этой функции, на котором определена функция f (x). Тогда, если функция f (x) имеет первообразную на множестве Х, то на множестве Т справедлива формула ò f(x)dx = ò f(φ(t))φ'(t)dt. Доказательство. Найдем дифференциалы обеих частей равенства: d (ò f(x)dx) = f(x)dx = f(φ(t))d(φ(t)) = f(φ(t))φ'(t)dt, d (ò f(φ(t)) φ'(t)dt) = f(φ(t))φ'(t)dt. Дифференциалы обеих частей равны, значит, сами интегралы могут отличаться лишь на постоянное слагаемое. При подходящем выборе функции φ(t) интеграл становится значительно проще исходного интеграла. Пример. Новую переменную можно не выписывать явно. В таких случаях говорят о введении постоянных и переменных под знак дифференциала или о тождественном преобразовании дифференциала. Пример 1. Пример 2. d (sin x) = cos х dx.
|
||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.184 (0.006 с.) |


 F 1 '(х 0 ) = f(х 0 ), касательные к графикам функций y = F 1 (x) и y = F 2 (x)
F 1 '(х 0 ) = f(х 0 ), касательные к графикам функций y = F 1 (x) и y = F 2 (x) 

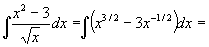
 .
.
 .
.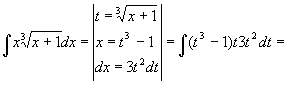
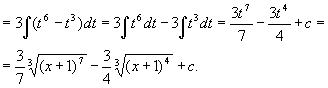
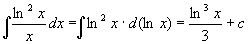 ,
,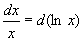 .
.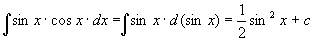 ,
,


