
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки существования пределаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
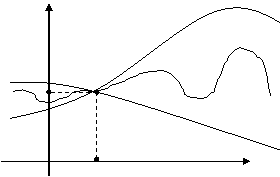
Признаки существования предела Теорема 1 (теорема о двух милиционерах). Если функцияy=f(x) в некоторой окрестности точки а заключена между двумя функциями
Теорема 2. Если функция y=f(x) монотонно возрастет (убывает) в некоторой окрестности точки а и ограничена сверху (снизу), то она имеет предел при Замечательные пределы Теорема 1. Предел отношения синуса малой дуги к самой дуге, выраженной в радианах, при стремлении величины дуги к нулю равен единице. Непрерывность функции в точке
Пусть функция y=f(x) определена в некоторой окрестности точки х 0. Определение 1. Функция y=f(x) называется непрерывной в точке х 0, если для любого Определение 2. Функция y=f(x) называется непрерывной на множестве А Ì R, если она непрерывна в каждой точке множества А. Сравнивая определение 1 с определением предела функции, можно получить, что функция y=f(x) непрерывна в точке х0 тогда и только тогда, когда ее предел при x ® х 0 равен значению функции в этой точке: Определение 3. Приращением аргумента называется разность двух значений переменной х и обозначается D х. Приращением функции, соответствующим данному приращению аргумента, называется разность двух значений функции от соответствующих аргументов и обозначается D у: D х = х-х 0, D у=f(x)-f(x 0 ). Из определения 1 следует: " Таким образом, функция непрерывна в точке тогда и только тогда, когда малому приращению аргумента соответствует малое приращение функции.
Теорема 2. Предел последовательности
Непрерывные проценты
Формула сложных процентов имеет вид где Q – сумма вкладов по истечении n периодов, Q 0 – первоначальный вклад, p – процент начисления за период. (Аналогичные формулы используют в демографических расчетах прироста населения и в экономических прогнозах увеличения валового национального продукта.) Пусть первоначальный депозит Q 0 помещен в банк под p= 100% годовых, через год сумма составит Предположим, что через полгода счет закрыт с результатом и эта сумма вновь помещена в качестве депозита в том же банке. В конце года депозит будет составлять Будем уменьшать срок размещения депозита в банке при условии его последующего размещения после изъятия. При ежеквартальном повторении этих операций депозит в конце года составит При ежемесячном повторении этих операций депозит в конце года составит При ежедневном повторении этих операций депозит в конце года составит При ежечасном повторении этих операций депозит в конце года составит и т. д. Последовательность значений увеличения первоначального вклада имеет предел при n®¥, равный е. Доход, который можно получить при непрерывном использовании процентов на проценты, может составить в год не более чем Если р – процент начисления и год разбит на n частей, то через t лет сумма депозита достигнет величины где Если ввести новую переменную Расчеты, выполненные по этой формуле, называют вычислениями по непрерывным процентам. Пример. Темп инфляции составляет 1% в день. Насколько уменьшится первоначальная сумма Q 0 через полгода? Инфляция уменьшит начальную сумму примерно в шесть раз.
Точки разрыва функции Функция является непрерывной в точке, если Определение 1. Точки, в которых нарушается условие непрерывности, называют точками разрыва функции. Определение 2. Точка разрыва х 0 называется точкой разрыва первого рода, если существуют конечные односторонние пределыв этой точке. Определение 3. Точка разрыва первого рода называется точкой устранимого разрыва, если односторонние пределы в этой точке равны. Определение 4. Скачком функции в точке разрыва первого рода называется модуль разности односторонних пределов в этой точке. Определение 5. Точка х 0 называется точкой разрыва второго рода, если она не является точкой разрыва первого рода (если хотя бы один из односторонних пределов не существует или равен +¥(-¥)). Пример 1. х =3 – точка устранимого разрыва. Связь между непрерывностью Свойства производных
Теорема 1. Производная постоянной функции равна нулю. Доказательство. f(x)=c,"x 0 Dy=f(x 0 +Dx) - f(x 0 )=c-c=0, Теорема 2. Если функции u, v, w дифференцируемы в некоторой точке, то и их алгебраическая сумма также дифференцируема в этой точке, причем производная алгебраической суммы равна алгебраической сумме производных и выполняется равенство Теорема 3. Если функции u и v дифференцируемы в некоторой точке, то и их произведение также дифференцируемо в этой точке, причем выполняется равенство Следствие. Постоянный множитель можно выносить за знак производной. Теорема 4. Если функции u и v дифференцируемы в некоторой точке и функция v в этой точке отлична от нуля, то существует производная частного в этой точке, причем Теорема 5 (производная сложной функции). Если функции y=f(z) и Теорема 6 (теорема Лагранжа). Конечное приращениедифференцируемой функции равно произведению соответствующего приращения аргумента на производную функции в некоторой промежуточной точке. Теорема 7 (теорема Ролля). Между двумя нулями дифференцируемой функции всегда найдется хотя бы один ноль производной. Доказательство. Пусть f(x 1 )=f(x 2 )= 0. Из теоремы Лагранжа следует, что найдется точка с, Две последние теоремы носят название теорем о конечных приращениях.
Дифференциал
Определение. Главная линейная относительно D х часть малого приращения функции называется дифференциалом функции и обозначается dy. Если малое приращение функции можно представить в виде Пример. Теорема. Функция не может иметь двух различных дифференциалов. Доказательство. Предположим противное – функция имеет два дифференциала. Тогда малое приращение функции можно представить в виде где Разделим обе части на D х: Переходя к пределу в обеих частях равенства при Полученное противоречие доказывает теорему. Связь между производной и дифференциалом Теорема 1. Если функция дифференцируема в некоторой точке, то в этой точке она имеет дифференциал. Доказательство. Функция По теореме о связи предела и б.м. функции: где Умножим обе части на D х: Следовательно, функция имеет дифференциал и Теорема 2. Если функция имеет дифференциал в некоторой точке, то она имеет производную в этой точке. Доказательство. Пусть функция имеет дифференциал Разделим обе части на D х: Переходя к пределу при Таким образом, функция имеет производную и Из этих теорем следует, что Дифференциал независимой переменной
Рассмотрим функцию у=х, dy=dx. Из теорем о связипроизводной и дифференциала следует, что: dy =1 · D x, dx = dy =D x. Дифференциал независимой переменной равен маломуприращению этой переменной. Таким образом, получена формула для вычисления дифференциала функции: Дифференциал функции равен произведению производной функции в данной точке на дифференциал независимой переменной. Экстремумы функции
Пусть функция y=f(x) определена на интервале (a,b). Определение 1. Точка х 0Î (a,b) называется точкой локального максимума (минимума) функции, если найдется некоторая окрестность этой точки, для всех точек которой будет выполняться условие: Точки локального максимума и минимума называют точками экстремума. Теорема 1 (необходимый признак экстремума функции). Если точка х 0 является точкой локального максимума (минимума) функции, то производная в этой точке равна нулю или не существует. Доказательство. Пусть функция y=f(x) дифференцируемана (a,b), " Дадим аргументу приращение Dx> 0 так, что Переходя к пределу при Дадим аргументу приращение Dx<0 так, что Переходя к пределу при Эти неравенства выполняются одновременно только в двух случаях: b) Следствие. В точке экстремума касательная: a) либо параллельна оси ОХ, b) либо не существует.
Данный признак не является достаточным для существования экстремума, т.е. из того, что производная равна нулю или не существует в некоторой точке, не следует, что в этой точке есть экстремум.
0 X 0 X y=x 3 y =
Точки, в которых первая производная равна нулю или не существует, называют критическими точками первой производной. Если функция имеет экстремумы, то они могут быть только в критических точках. Пусть функция y=f(x) определена и непрерывна в некоторойокрестности точки х 0 и дифференцируема в этой окрестности (за исключением, быть может, точки х 0). Теорема 2 (достаточный признак экстремума). Если первая производная функции в точке х 0 равна нулю или не существует и при переходе через нее производная меняет знак, то данная точка является точкой экстремума, причем если знак меняется с ''+'' на ''-'', то это точка максимума, с ''-'' на ''+'' – точка минимума. Доказательство. Пусть в точке х 0 производная дифференцируемой функции равна нулю или не существует и при переходе через нее производная меняет знак с ''+'' на ''-''.
Следовательно, х 0 - точка максимума. Случай минимума рассматривается аналогично. Экстремумы функции
Пусть функция y=f(x) определена на интервале (a,b). Определение 1. Точка х 0Î (a,b) называется точкой локального максимума (минимума) функции, если найдется некоторая окрестность этой точки, для всех точек которой будет выполняться условие: Точки локального максимума и минимума называют точками экстремума. Теорема 1 (необходимый признак экстремума функции). Если точка х 0 является точкой локального максимума (минимума) функции, то производная в этой точке равна нулю или не существует. Доказательство. Пусть функция y=f(x) дифференцируемана (a,b), " Дадим аргументу приращение Dx> 0 так, что Переходя к пределу при Дадим аргументу приращение Dx<0 так, что Переходя к пределу при Эти неравенства выполняются одновременно только в двух случаях: b) Следствие. В точке экстремума касательная: a) либо параллельна оси ОХ, b) либо не существует.
Данный признак не является достаточным для существования экстремума, т.е. из того, что производная равна нулю или не существует в некоторой точке, не следует, что в этой точке есть экстремум.
0 X 0 X y=x 3 y =
Точки, в которых первая производная равна нулю или не существует, называют критическими точками первой производной. Если функция имеет экстремумы, то они могут быть только в критических точках. Пусть функция y=f(x) определена и непрерывна в некоторойокрестности точки х 0 и дифференцируема в этой окрестности (за исключением, быть может, точки х 0). Теорема 2 (достаточный признак экстремума). Если первая производная функции в точке х 0 равна нулю или не существует и при переходе через нее производная меняет знак, то данная точка является точкой экстремума, причем если знак меняется с ''+'' на ''-'', то это точка максимума, с ''-'' на ''+'' – точка минимума. Доказательство. Пусть в точке х 0 производная дифференцируемой функции равна нулю или не существует и при переходе через нее производная меняет знак с ''+'' на ''-''.
Следовательно, х 0 - точка максимума. Случай минимума рассматривается аналогично. Выпуклость графика функции. Точки перегиба графика
Определение 1. График функции y=f(x) называется выпуклым (вогнутым) на интервале (a,b), если касательная к графику, проведенная в любой точке этого интервала, расположена над (под) графиком функции.
Теорема 1. Если вторая производная дваждыдифференцируемой функции на некотором интервале отрицательна (положительна), то график функции на данном интервале выпуклый (вогнутый). Верна и обратная теорема. Определение 2. Точки, в которой график функции меняет направление выпуклости, называют точками перегиба графика функции. Y
y=f(x)
0 a c X
Точка a является точкой перегиба, а точка c нет, так как в этой точке функция не дифференцируема. Теорема 2. (необходимый признак точки перегиба). Если точка х 0 является точкой перегиба графика дважды дифференцируемой функции, то в этой точке вторая производная равна нулю: Определение 3. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками второй производной. Если функция имеет точки перегиба, то они могут быть только в критических точках. Теорема 3 (достаточный признак точки перегиба). Если вторая производная дважды дифференцируемой функции в некоторой точке равна нулю и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба. Асимптоты графика функции
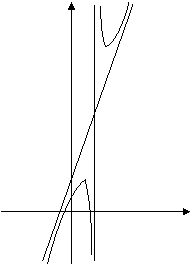
Графики некоторых функции расположены на плоскости так, что они неограниченно приближаются к некоторой прямой. Эти прямые называются асимптотами к графику функции. Определение 1. Прямая х=а называется вертикальной асимптотой к графику функции y=f(x), если хотя бы один изодносторонних пределов Как правило, в точке а функция терпит разрыв второго рода. Определение 2. Прямая у=b называется горизонтальной асимптотой к графику функции y=f(x), если Определение 3. Прямая у=kx+b называется наклонной асимптотой к графику функции y=f(x), если функцию можно представить в виде f(x)=kx+b+ Найдем параметры наклонной асимптоты. 1. Найдем k. f(x)=kx+b+ Разделим обе части равенства на х. Переходя к пределу при 2. Найдем b. f(x)=kx+b+ b+ Переходя к пределу при Если k=0 и b¹0, то наклонная асимптота становится горизонтальной. Пример. х= 1 – вертикальная асимптота. горизонтальной асимптоты нет. k = b = y= 3 x+ 3 – наклонная асимптота.
Метод замены переменной В неопределенном интеграле
Теорема 1. Пусть функция х = φ (t) определена идифференцируема на некотором промежутке Т, а Х – множество значений этой функции, на котором определена функция f (x). Тогда, если функция f (x) имеет первообразную на множестве Х, то на множестве Т справедлива формула ò f(x)dx = ò f(φ(t))φ'(t)dt. Доказательство. Найдем дифференциалы обеих частей равенства: d (ò f(x)dx) = f(x)dx = f(φ(t))d(φ(t)) = f(φ(t))φ'(t)dt, d (ò f(φ(t)) φ'(t)dt) = f(φ(t))φ'(t)dt. Дифференциалы обеих частей равны, значит, сами интегралы могут отличаться лишь на постоянное слагаемое. При подходящем выборе функции φ(t) интеграл становится значительно проще исходного интеграла. Пример. Новую переменную можно не выписывать явно. В таких случаях говорят о введении постоянных и переменных под знак дифференциала или о тождественном преобразовании дифференциала. Пример 1. Пример 2. d (sin x) = cos х dx. В неопределенном интеграле
Теорема. Пусть функции u и υ определены идифференцируемы на некотором промежутке Т и функция du·υ имеет на этом промежутке первообразную. Тогда функция u · dυ также имеет первообразную на промежутке Т, причем справедлива формула ò udυ = uυ - ò υdu. Доказательство. Найдем дифференциал от их произведения u · υ. d(uυ) = du·υ + u·dυ. Проинтегрируем обе части этого равенства. ò d(uυ) = ò (du·υ + u·d υ). uυ = ò υdu + ò udυ, ò udυ = uυ - ò υdu - формула интегрирования по частям. С помощью этой формулы первообразная частично находится, и оставшиеся интегральные слагаемые, как правило, - проще исходного интеграла. Данная формула применяется к интегралам следующих видов. 1) где P(x) - многочлен, его выбирают в качестве u. 2) В качестве u выбирают трансцендентную функцию. 3) Циклические интегралы – это те, в которых подынтегральная функция представляется в виде произведения двух функций, мало меняющихся при интегрировании и дифференцировании. Пример 1. Пример 2. =
Определенный интеграл
Пусть функция у = f(x) определена, непрерывна(следовательно, ограничена) на [ a,b ]. Разобьем отрезок [ a,b ] на n произвольных частей точками a = x 0 < x 1 < x 2 < … < x n = b. Длину i -го отрезка разбиения обозначим D х i= x i - x i-1, i = Внутри i -го отрезка разбиения выберем по произвольной точке сi
с 1 с 2 с 3 с n
х 0 х 1 х 2 х 3 х n-1 х n a b
и составим сумму Определение 1. Сумма вида (1) называется интегральной суммой функции f(x) по отрезку [ a,b ]. Определение 2. Если существует конечный пределинтегральных сумм вида (1) при уменьшении длин отрезков разбиения, то он не зависит от способов разбиения отрезка. Этот предел называется определенным интегралом от функции f(x) по отрезку [ a,b ] и обозначается Геометрический смысл Определенного интеграла
Пусть функция у = f(x) определена и непрерывна на [ a,b ]. Разобьем отрезок [ a,b ] на n частей точками, в каждом отрезке разбиения возьмем по точке с i и составим интегральную сумму Выясним, что представляет собой геометрически интегральная сумма.
y=f(x)
c 1 c 2 c n 0 x 0= a x 1 x 2 x n-1 x n= b Х
Из рисунка видно, что интегральная сумма равна площади ступенчатой фигуры, вписано–описанной около графика функции. При измельчении длин отрезков разбиения площадь этой фигуры будет неограниченно приближаться к площади фигуры, заключенной между графиком функции и осью О Х на отрезке [ а,b ]. С другой стороны, предел интегральной суммы вида (1) при измельчении длин отрезков разбиения равен определенному интегралу Несобственные интегралы
При определении определенного интеграла предполагалось, что: 1) отрезок интегрирования конечен; 2) функция непрерывна на отрезке интегрирования. Если нарушено одно из этих условий, то определенный интеграл называется несобственным, причем если отрезок интегрирования неограничен, то интеграл называется несобственным интегралом первого рода, если же функция не ограничена на отрезке интегрирования, то несобственным интегралом - второгорода. С геометрической точки зрения, несобственные интегралы выражают площади неограниченных фигур. Некоторые приложения Задача дисконтирования Задача дисконтирования состоит в определении начальной суммы S через время t по ее конечной величине S tпри процентной ставке p. При непрерывном начислении процента конечная сумма вычисляется по формуле где r=p /100. Если сумма S t также является функцией времени S t= f(t), то дисконтированная сумма к моменту времени t составит Полная дисконтированная сумма за время t вычисляется по формуле Пример. Определить дисконтированную сумму S dпри f(t)=S 0 (1+kt), где S 0 – начальные капиталовложения, k – ежегодная доля их увеличения. Другими словами, при заданных p и k требуется оценить, что выгоднее: наращивать капиталовложения или вложить их одновременно при непрерывно начисляемой процентной ставке.
Из полученной формулы следует, что: 1) чем выше процентная ставка р (а значит, r), тем меньше дисконтная сумма S d и, следовательно, выше доход. Если рассматривать S d как дисконтный доход, то увеличение процентной ставки р снижает рентабельность помещения капитала; 2) увеличение интенсивности ежегодных капиталовложений k приводит к увеличению S d; 3) при неизменных k и p дисконтный доход растет с увеличением промежутка времени t. Непрерывность функции Многих переменных
Рассмотрим функцию двух переменных n=2; z=f(x,y). Возьмем точку (х 0 ,у 0 ) называется частным приращением функции по переменной х. Аналогично, фиксируя х 0 и давая аргументу у приращение |

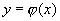 и
и 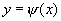 , т.е. выполняется неравенство
, т.е. выполняется неравенство 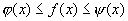 "х, причем эти функции имеют одинаковый предел при
"х, причем эти функции имеют одинаковый предел при 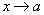 , то существует предел функции y=f(x) при
, то существует предел функции y=f(x) при 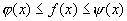 ,
,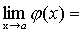
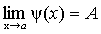 =>
=> 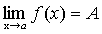 .
.
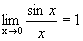 .
.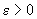 найдется
найдется 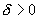 такое, что при всех х, удовлетворяющих неравенству
такое, что при всех х, удовлетворяющих неравенству 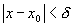 , будет выполняться неравенство
, будет выполняться неравенство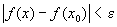 .
.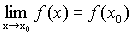 .
.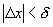 будет выполняться
будет выполняться 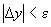 , т.е.
, т.е.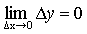 .
.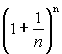 при
при 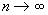 равен
равен 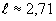 .
.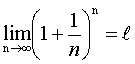 ,
, 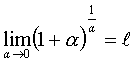 .
.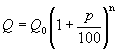 ,
,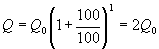 .
.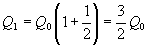 ,
,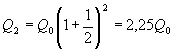 .
.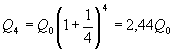 .
.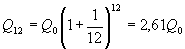 .
.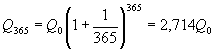 .
.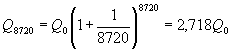

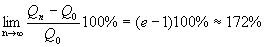 .
.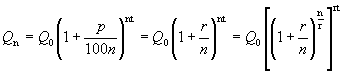 ,
,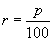 .
.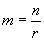 , то при n®¥ Þ m®¥.
, то при n®¥ Þ m®¥.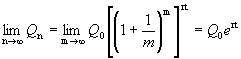 .
.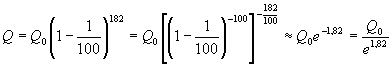 .
.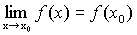 ó
ó 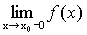 =
= 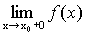
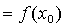 .
.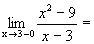 ,
,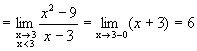
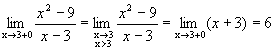 ,
,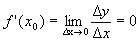 .
.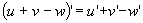 .
.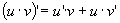 .
.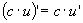 .
.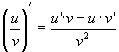 .
.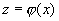 - дифференцируемые функции своих аргументов, то и их композиция является дифференцируемой функцией, причем производная сложной функции равна производной внешней функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной.
- дифференцируемые функции своих аргументов, то и их композиция является дифференцируемой функцией, причем производная сложной функции равна производной внешней функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной.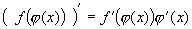 .
.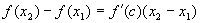 .
.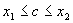 , такая, что
, такая, что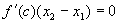 =>
=> 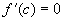 .
.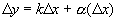 , где
, где 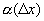 - б.м. функция более высокого порядка, чем D х при
- б.м. функция более высокого порядка, чем D х при 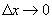 (
( 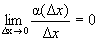 ), тогда
), тогда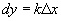 .
.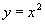 .
.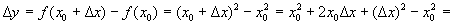
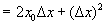 ,
,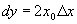 .
.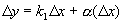 ,
,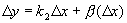 ,
,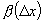 - б.м. функции более высокого порядка, чем D х при
- б.м. функции более высокого порядка, чем D х при 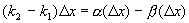 .
.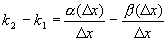 .
.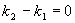 ,
,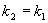 .
.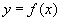 - дифференцируема в точке х 0,
- дифференцируема в точке х 0,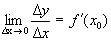 .
.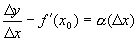 ,
,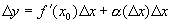 ,
,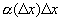 - б.м. функция более высокого порядка, чем Dх.
- б.м. функция более высокого порядка, чем Dх.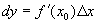 .
.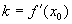 .
.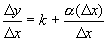 .
.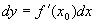 .
.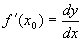 .
.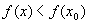 (
( 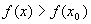 ).
).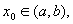 найдется число d такое, что:
найдется число d такое, что: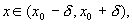
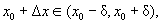
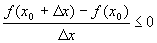 .
.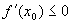 .
.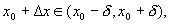
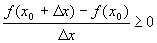 .
.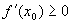 .
.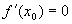 ,
,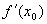 не существует.
не существует.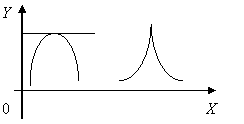
 YY
YY
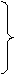
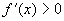
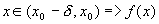 возрастает на
возрастает на 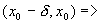
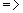
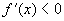
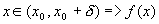 убывает на
убывает на 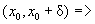
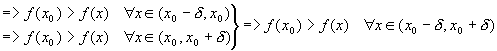 .
.
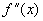 <0.
<0. 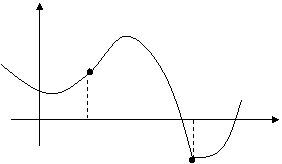
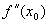 =0.
=0.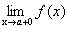 ,
, 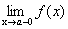 равен +¥ или -¥.
равен +¥ или -¥.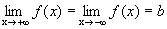 .
.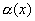 , где
, где 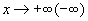 .
.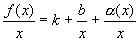 .
.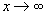 , получим
, получим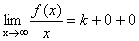 ,
,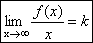 .
.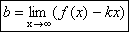 .
.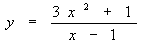 .
.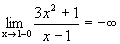 ,
,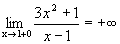 ,
,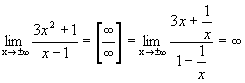 ,
,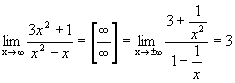 ,
,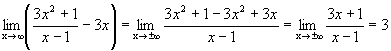 ,
,
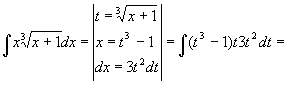
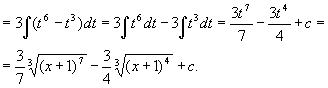
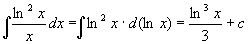 ,
,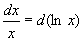 .
.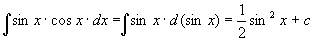 ,
,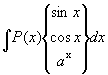 ,
,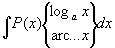 .
.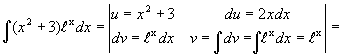
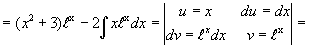
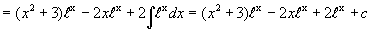 .
.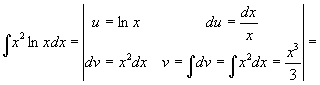
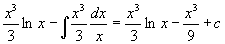 .
.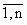 .
.

 Х
Х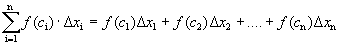 . (1)
. (1)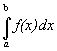 .
.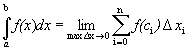 .
.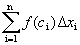 . (1)
. (1)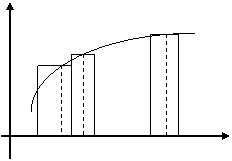 Y
Y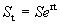 ,
,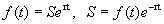 .
.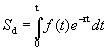 .
.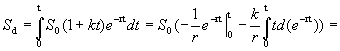
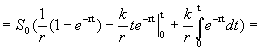
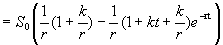 .
.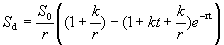 .
. D(у)
D(у) 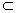 R 2. Дадим аргументу х в данной точке приращение
R 2. Дадим аргументу х в данной точке приращение 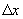 , зафиксировав у 0. Выражение
, зафиксировав у 0. Выражение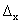 z=f(x0+
z=f(x0+ 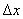 ,y0) - f(x0,y0)
,y0) - f(x0,y0)


