
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие функции многих переменных ⇐ ПредыдущаяСтр 4 из 4
Пусть даны множества D Определение 1. Если каждой точке Если зафиксировать любые n -1 переменные, то функция многих переменных превращается в функцию одной переменной. x 2= с 2, x 3= с 3, …, х n= c n; y=f (x 1, c 2, …, c n) - функция одной переменной х 1. Пример. Определение 2. Графиком функции двух переменных z=f(x,y) называется множество точек (х, у, z) 3-мерного пространства, таких, что (х, у)
0 Y X Определение 3. Графиком функции n переменных называется n -мерная гиперповерхность в пространстве R n +1, точки которой имеют вид (х1, х2, …, хn, f(x1, х2, …, xn)). Определение 4. Линией уровня функции двух переменных называется линия на плоскости XOY, принадлежащая D (z), в каждой точке которой функция принимает одно и то же значение. Уравнение линии уровня: f(x, y) = c, где с - произвольное число. На данной линии уровня значение функции z=c. Линий уровня бесконечно много, и через каждую точку области определения можно провести линию уровня. Пример. z(x,y) = D(z) = R 2\{(1,1)}.
Z=1 Z=4 1 Z=9 0 1 X c =1, c =4, c =9, Используя линии уровня, можно построить график функции.
Z 0 Y X Определение 5. Поверхностью уровня функции n переменных y=f(х 1, х 2, …, х n ) называется гиперповерхность в пространстве R n, входящая в D (у), в каждой точке которой значение функции одно и то же. Уравнение поверхности уровня f(х 1, х 2, …, х n )=с. На поверхности уровня значение функции постоянно: у=с. Непрерывность функции Многих переменных
Рассмотрим функцию двух переменных n=2; z=f(x,y). Возьмем точку (х 0 ,у 0 ) называется частным приращением функции по переменной х. Аналогично, фиксируя х 0 и давая аргументу у приращение Выражение
называется полным приращением функции. Определение 1. Функция z=f(x, y) называется непрерывной в точке (x 0, y 0) Определение 2. Функция z=f(x, y) называется непрерывной на множестве А Частные производные функции Многих переменных
Рассмотрим функцию двух переменных n=2; z=f(x,y). Определение. Частной производной функции z=f(x,y) в точке(x 0, y 0) При введении частной производной по любой переменной остальные переменные были фиксированы. Данное определение совпадает с определением производной функции одной переменной. Следовательно, частную производную можно найти, зафиксировав все переменные, кроме одной, считая их постоянными. Производная находится как производная функции одной переменной, т.е. Пример 1. Пример 2. Полный дифференциал
Определение. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции. Рассмотрим функцию двух переменных n=2; z=f(x,y). Если приращение функции где Теорема. Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных. Пример. Производная по направлению
Рассмотрим функцию двух переменных n=2; z=f(x, y). Под направлением мы будем понимать любой вектор
0 Определение 1. Направляющими косинусами данного направления
Направляющие косинусы любого направления в любом пространстве обладают следующим свойством: сумма квадратов направляющих косинусов равна единице. На плоскости имеем Если рассмотреть вектор Пусть даны точка
Dx
0
Функция получит приращение, которое называется приращением функции в данном направлении: Из треугольника М0 М1 А: Из треугольника М0 М1 В: Определение 2. Предел отношения приращения функции в данном направлении к приращению направления, когда приращение направления стремится к нулю, называется производной функции в данном направлении (если этот предел существует и конечен); Если направление Теорема. Производная по направлению равна сумме попарных произведений частных производных в данной точке на направляющие косинусы данного направления.
Пример. Найти производную функции
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.203.68 (0.027 с.) |
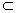 R n и I
R n и I 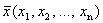 множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f (x 1, …, x n). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I.
множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f (x 1, …, x n). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I.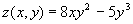 - функция двух переменных,
- функция двух переменных, - функция трех переменных.
- функция трех переменных.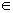 D (z) и z = f (x, y). Любую точку графика можно записать в виде (х, у, f (x, y)).
D (z) и z = f (x, y). Любую точку графика можно записать в виде (х, у, f (x, y)). Z
Z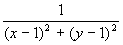 ,
,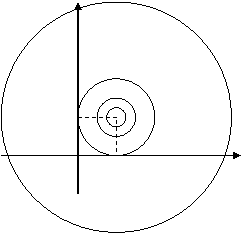 Y Z=1/9
Y Z=1/9 , z=1.
, z=1. , z=4.
, z=4. , z=9.
, z=9.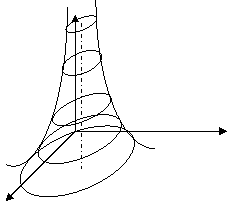
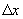 , зафиксировав у 0. Выражение
, зафиксировав у 0. Выражение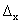 z=f(x0+
z=f(x0+ 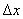 ,y0) - f(x0,y0)
,y0) - f(x0,y0) , мы получим частное приращение по переменной у.
, мы получим частное приращение по переменной у. z=f(x0,y0+
z=f(x0,y0+  ) - f(x0, y0).
) - f(x0, y0). z=f(x0+
z=f(x0+  .
. ,
, .
. . Все правила и формулы, справедливые для производной функции одной переменной, остаются справедливыми и для частных производных.
. Все правила и формулы, справедливые для производной функции одной переменной, остаются справедливыми и для частных производных.
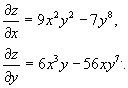


 можно представить в виде
можно представить в виде ,
, - бесконечно малые функции при
- бесконечно малые функции при 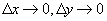 , соответственно, то выражение
, соответственно, то выражение 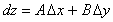 называется полным дифференциалом функции двух переменных.
называется полным дифференциалом функции двух переменных. .
. .
.
 на плоскости.
на плоскости. Y
Y

 b
b 
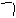 a
a
 X
X .
.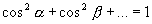 .
. .
. .
. , координатами которого являются направляющие косинусы данного направления, то этот вектор сонаправлен с вектором
, координатами которого являются направляющие косинусы данного направления, то этот вектор сонаправлен с вектором 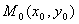 и направление
и направление  Y M 1
Y M 1 B b
B b  X
X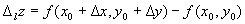 ,
, .
. .
. .
.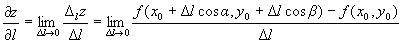 .
.
 .
. в точке М (1, 2) в направлении
в точке М (1, 2) в направлении 


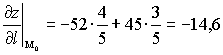 .
.


