
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность обратной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть Теорема 3.11 Пусть Доказательство. Во-первых, заметим, что если Во-вторых, пусть
Таким образом, если Непрерывность сложной функции. Введём понятие сложной функции. Пусть функции Теорема. Если функция z=f(y) непрерывна в точке ○ Пусть задано произвольное число
где В силу непрерывности функции можно указать число
Из условий (2) и (2') следует, что на множестве
где
Это означает, в силу определения непрерывности, что функция 49) Непрерывность элементарных функций Целая и дробная рациональные функции. Непрерывность f(x)=const и f(x)=x непосредственно ясна. На основании теоремы о произведении непрерывных функций вытекает непрерывность любого одночленного выражения axm, по теореме о сумме непрерывных функций - непрерывность многочлена a0xn + a1xn-1 +... +an-1 + an. Непрерывность данных функций имеет место на всем интервале Показательная функция y=ax(a>1) монотонно возрастает на всем интервале Логарифмическая функция Степенная функция Тригонометрические функции Обратные тригонометрические функции 50) Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1031; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

 -- функция, непрерывная на отрезке
-- функция, непрерывная на отрезке  . Предположим, что
. Предположим, что  следует, что
следует, что  . Тогда образом отрезка
. Тогда образом отрезка  , где
, где  и
и 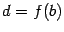 (действительно, непрерывная функция принимает любое промежуточное между
(действительно, непрерывная функция принимает любое промежуточное между  и
и  значение, причём ровно один раз, что следует из монотонности). Поэтому существует обратная к
значение, причём ровно один раз, что следует из монотонности). Поэтому существует обратная к  функция
функция  функция, действующая из
функция, действующая из  монотонно возрастает. (Если бы функция
монотонно возрастает. (Если бы функция  была монотонно убывающей, то и обратная к ней функция
была монотонно убывающей, то и обратная к ней функция  ,
,  . Тогда обратная к
. Тогда обратная к  ,
,  , то
, то  .
. ; рассмотрим функцию
; рассмотрим функцию  , которая определена при
, которая определена при  . Очевидно, что
. Очевидно, что  -- непрерывная на
-- непрерывная на  функция, поэтому она принимает наименьшее значение
функция, поэтому она принимает наименьшее значение  в некоторой точке
в некоторой точке  :
:
 , то
, то  , то есть если
, то есть если  , то
, то  . Последнее утверждение можно переформулировать так: для любого числа
. Последнее утверждение можно переформулировать так: для любого числа  найдётся число
найдётся число  , такое что при
, такое что при  выполняется неравенство
выполняется неравенство  . (При этом
. (При этом  ,
,  ,
,  ,
,  .) Получили, что функция
.) Получили, что функция  и
и  определены на множестве X и Y соответственно, причём множество значений функции
определены на множестве X и Y соответственно, причём множество значений функции  содержится в области определения функции f Тогда функцию, принимающую при каждом
содержится в области определения функции f Тогда функцию, принимающую при каждом  значение
значение  , называют сложной функцией или суперпозицией (композицией) функций
, называют сложной функцией или суперпозицией (композицией) функций  .
. , а функция
, а функция  , причём
, причём  , то в некоторой окрестности точки
, то в некоторой окрестности точки  , и эта функция непрерывна в точке
, и эта функция непрерывна в точке  . В силу непрерывности функции f в точке
. В силу непрерывности функции f в точке  такое, что
такое, что  и
и (2)
(2) .
.
 такое, что
такое, что (2')
(2') определена сложная функция
определена сложная функция  ,
, , т.е.
, т.е. .
. .●
.● . Частное двух многочленов
. Частное двух многочленов  непрерывно всюду, кроме точек b0xm + b1xm-1 +...+ bm-1x + bm = 0 (в этих точках - либо разрыв 2-го рода, либо устранимый разрыв).
непрерывно всюду, кроме точек b0xm + b1xm-1 +...+ bm-1x + bm = 0 (в этих точках - либо разрыв 2-го рода, либо устранимый разрыв). . Из существования логарифма следует непрерывность данной функции.
. Из существования логарифма следует непрерывность данной функции. . Рассмотрим случай a>1. Эта функция возрастает при
. Рассмотрим случай a>1. Эта функция возрастает при  , и принимает любое значение из
, и принимает любое значение из  . Отсюда следует ее непрерывность.
. Отсюда следует ее непрерывность. . При возрастании x от 0 до
. При возрастании x от 0 до  возрастает
возрастает  или убывает
или убывает  на интервале
на интервале  ,
,  ,
,  ,
,  ,
,  ,
,  . Остановимся на функции
. Остановимся на функции  вытекает из ее монотонности, а также из факта (устанавливаемого геометрически), что при этом она принимает все значения от -1 до 1. То же относится к любому промежутку
вытекает из ее монотонности, а также из факта (устанавливаемого геометрически), что при этом она принимает все значения от -1 до 1. То же относится к любому промежутку  . Следовательно, функция
. Следовательно, функция  . Исключение для первых двух функций - значения x вида
. Исключение для первых двух функций - значения x вида  , при которых
, при которых  , для других двух - значения вида
, для других двух - значения вида  , при которых
, при которых  .
. ,
,  ,
,  ,
,  . Первые две непрерывны на
. Первые две непрерывны на  , остальные - на
, остальные - на 






