
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найдите предел функций в точке.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОСТОВСКИЙ-НА-ДОНУ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ И ИНФОРМАТИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ по выполнению практических работ по дисциплине «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»
Для студентов 2 курсов Банковское дело
Одобрена цикловой комиссий. У тверждаю М и ЕН Зам. директора по УР Протокол №__от______2008г Председатель ЦК М и ЕН _______________ Жукова Е.Л. _______________ Лебединская А.Р.
Составитель: Шмидт Т.Ю. Преподаватель РКСИ
Практическая работа №1 «Вычисление пределов функции. Классификация точек разрыва». Цель: формирование умения решать задачи на нахождение пределов функции, исследовать функцию на непрерывность, классифицировать точки разрыва.
Теоретическая часть Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа e существует номер N, что все значения xn , у которых n>N, удовлетворяют неравенству
Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся. Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n. Число А называется пределом функции f(x) при х→х0 , если для
В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной. Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной. Можно также находить пределы функции на бесконечности. Определение. Число A называется пределом функции y=f(x) на бесконечности (или при х, стремящемся к бесконечности), если для всех достаточно больших по модулю значений аргумента х соответствующие значения функции f(x) сколь угодно мало отличаются от числа A.
На рис.1 изображен график функции
Замечание. Выражения вида 0/0, ¥ /¥, 0 × ¥, ¥ - ¥, Основные теоремы о пределах функции:
Первый замечательный предел функции:
Второй замечательный предел функции:
Удобно пользоваться также следующими следствиями замечательных пределов:
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п. Функция f(x) называется непрерывной в точке х 0, если она непрерывна в некоторой окрестности точки х 0 (следовательно, и в самой точке х 0), существует предел функции при х→х0 и он равен значению функции в этой точке:
Если равенство нарушено, то говорят, что при x = xo функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множествоR, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(xo)= f(0) не определено, поэтому в точке xo = 0 функция имеет разрыв. Функция f(x) называется непрерывной справа в точке xo, если
и непрерывной слева в точке xo, если
Непрерывность функции в точке xo равносильна ее непрерывности в этой точке одновременно и справа и слева. Для того чтобы функция была непрерывна в точке xo, например, справа, необходимо, во-первых, чтобы существовал конечный предел 1. Точка х=х0 называется точкой разрыв первого рода, если в этой точке функция имеет конечные, но различные одностороннее пределы. А разность
2. Точка х=х0 называется точкой устранимого разрыва, если в этой точке функция имеет равные между собой конечные пределы, но сама в этой точке либо принимает другое значение, либо вообще не определенна. 3. Если Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой. Практическая часть Пример 1. Найти Решение. Применяя теорему 1 о пределе разности и произведения, находим предел знаменателя: Предел знаменателя не равен нулю, поэтому, по теореме 1 о пределе частного, получаем: Ответ: 1,5 Пример 2. Найдите предел функции Решение. Пределы числителя и знаменателя при х→3 равны нулю. Для раскрытия неопределенности
Ответ: Пример 3. Найдите предел функции Решение. При х →∞ числитель и знаменатель – величины бесконечно большие. Имеем неопределенность вида
Примечание. Ответ: Пример 4. Найдите предел функции Решение. Примечание. Можно также использовать следствие из первого замечательного предела Ответ: 3 Пример 5. Найдите предел функции Решение. Ответ: е4. Пример 6. Найти Решение. Разделим числитель и знаменатель на х.
Примечание. Было применено следствие из второго замечательного предела Ответ: е-4 . Пример 7. Найти Решение. Применять теорему о пределе разности нельзя, поскольку имеем неопределенность вида ¥ - ¥. Умножим и разделим общий член на его сопряженное:
Ответ: 1 . Пример 8. Найти Решение. Обозначим arcsin x=t. Тогда x=sin t и при x®0 t®0.
Ответ: 1 Пример 9. Найти Решение. При х→0 числитель и знаменатель стремятся к нулю. Для раскрытия неопределенности умножим и числитель и знаменатель на сопряженное знаменателя.
Ответ: Пример 10. Исследовать на непрерывность и построить график функции
Решение. Функции у=х3+1, у=2, у=3х являются непрерывными на всей числовой прямой, поэтому точку разрыва функция может иметь только в точках х=1, х=2. Исследуем функцию на непрерывность в этих точках. х=1. Найдем односторонние пределы:
Т.о. в точке х=1 функция не имеет точек разрыва. Аналогично, для точки х=2 имеем:
Как видим,
Скачок функции функции f(x) в точке х=2 равен
График функции изображен на рис.2. Практические задания ПРАКТИЧЕСКАЯ РАБОТА №2
«Правила дифференцирования. Производная сложной функции» Цель: сформировать навыки нахождения производных элементарных и сложных функций,применять основные правила дифференцирования.
Теоретическая часть Понятие производной является основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в 17 и 18вв. С возникновением этого метода связаны имена двух великих математиков—И. Ньютона и Г.В. Лейбница. Возникло дифференциальное исчисление при решений задач о мгновенной скорости движения материальной точки. Рассмотрим неравномерное движение материальной точки. Средняя скорость ее за промежуток времени Δt равна
Эта и другие задачи приводят к понятию производной функции. Отношение
Определение. Производной функции y=f(x) в точке х называется предел отношения приращения функции ∆y к приращению аргумента ∆x, когда приращение аргумента стремится к нулю:
Функция может иметь производную в точке х0 только тогда, когда функция определена и непрерывна во всех точках некоторой окрестности х0 и говорим, что функция дифференцируема в этой точке. Правила дифференцирования. Пусть даны функции u, v и w. 1. Производная суммы (разности) равна сумме (разности) производных: (u+v-w)/ = u/+v/-w/ . 2. Производная произведения: (uv)/ =u/v+uv/. 3. Производная частного: 4. Постоянный множитель можно вынести за знак производной: (Cu)/=Cu/. 5. Производная постоянной равна нулю: C/=0, Практическая часть Пример 1. Вычислить производную функции: а) у=(5-x2+x3)(x4-3); б) Решение. а) Применим правило дифференцирования (2) ((5-x2+x3)(x4-3))/=(5-x2+x3)/(x4-3)+(5-x2+x3)(x4-3)/=(-2x+3x2)(x4-3)+(5-x2+x3)∙4x3=-2x5+6x+3x6-9x2+20x3-4x5+4x6=7x6-6x5+20x3-9x2+6x. б) Применим правило дифференцирования (3)
в) Применим правило нахождения производной сложной функции ((x4-5x3+7)5)/=5∙(x4-5x3+7)4∙(x4-5x3+7)/=5∙(x4-5x3+7)4(4x3-15x2)=(20x3-75x2)(x4-5x3+7). Пример 2. Вычислить производную функции Решение. Применим свойство (3) и правило нахождения сложной функции: Пример 3. Найти производную функции Решение.
Практические задания Найти производные функции:
Контрольные вопросы Практическая работа № 3
«Раскрытие неопределенностей. Правило Лопиталя» Цель работы: Научится раскрывать неопределенности с помощью правила Лопиталя. Теоретическая часть (Лопиталь (1661-1704) – французский математик) К разряду неопределенностей принято относить следующие соотношения:
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
Аналогично можно применить правило Лопиталя при раскрытии неопределенности
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя. Практическая часть Пример 1: Найти предел Решение. Как видно, при попытке непосредственного вычисления предела получается неопределенность вида f¢(x) = 2x +
Пример 2: Найти предел Решение. Числитель и знаменатель при х=0 равны нулю, т.е. имеем неопределенность
Пример 3: Найти предел Решение.
- получили неопределенность. Применяем правило Лопиталя еще раз.
Пример 4: Найти предел Решение. Здесь имеем неопределенность вида
Пример 5: Найти предел Решение. В данном примере имеется неопределенность вида
Практические задания Найдите пределы, используя правило Лопиталя.
Контрольные вопросы:
Практическая работа №4 «Дифференциал функции. Приближенные вычисления » Цель работы: Научится находить дифференциал функции. Находить приближенные значения функции с помощью дифференциала». Теоретическая часть Пусть функция y = f(x) имеет производную в точке х:
Тогда можно записать: Следовательно: Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу. Определение. Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции. Обозначается dy или df(x). Из определения следует, что dy = f¢(x)Dx. Для функции х производная равна 1, и потому ее дифференциал равен ∆х, dy = f¢(x)dx. (1)
Можно также записать:
Свойства дифференциала. Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv 2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv 3) d(Cu) = Cdu 4) 5) С помощью дифференциала можно найти приближенные значения функции. Учитывая, что
Это означает, что приближенное значение функции вблизи точки х0 равно сумме ее значения в этой точке и дифференциала в этой же точке.
Практическая часть. Пример1. Найдите дифференциал функции: а) в) <
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.252.239 (0.012 с.) |

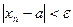 .
.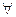 ε>0
ε>0 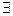 такое δ >0, что для всех х, удовлетворяющих условиям |х-х0|<δ, х≠х0, имеет место неравенство |f(x)-A|<ε.
такое δ >0, что для всех х, удовлетворяющих условиям |х-х0|<δ, х≠х0, имеет место неравенство |f(x)-A|<ε.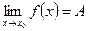


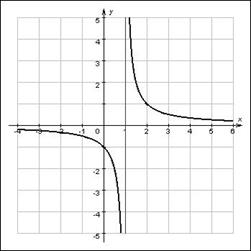 рис.1
рис.1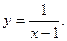 Видно, что ординаты изображающие значения функции, сколь угодно мало отличаются от числа 0 для любых достаточно больших значений х, т.е.
Видно, что ординаты изображающие значения функции, сколь угодно мало отличаются от числа 0 для любых достаточно больших значений х, т.е.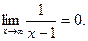
 являются неопределенными и нахождение пределов такого вида носит название “раскрытие неопределенностей”.
являются неопределенными и нахождение пределов такого вида носит название “раскрытие неопределенностей”.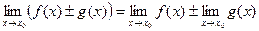 ,
, ,
,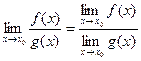
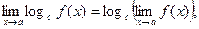 где c=const.
где c=const.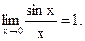
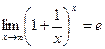 .
.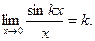
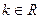 ;
;  ,
, 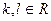 ;
;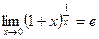 ;
; 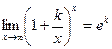 ,
, 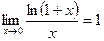 .
.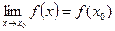 .
.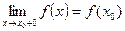 ,
,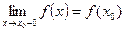 .
.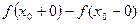 называется скачком функции в точке х0.
называется скачком функции в точке х0. равен ∞ или не существует, то говорят, что в точке xo функция имеет разрыв второго рода.
равен ∞ или не существует, то говорят, что в точке xo функция имеет разрыв второго рода.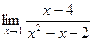 .
.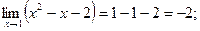
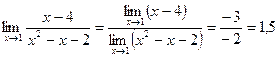 .
.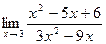 .
. разложим на множители числитель и знаменатель и сократим дробь.
разложим на множители числитель и знаменатель и сократим дробь.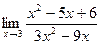 =
= 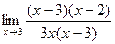 =
= 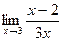 =
= 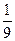 .
.
 .
.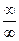 . Для раскрытия неопределенности числитель и знаменатель нужно разделить на х3:
. Для раскрытия неопределенности числитель и знаменатель нужно разделить на х3:



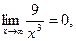
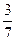 .
. .
.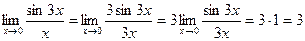 .
. .
. .
.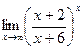 .
.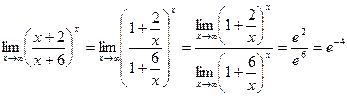 .
. .
.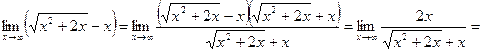
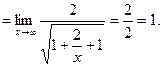
 .
.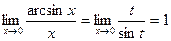 .
.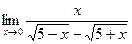 .
.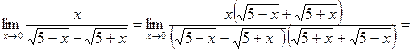
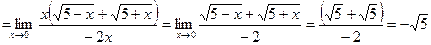 .
.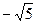 .
.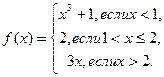


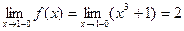 ,
, 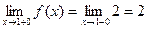 .
. ,
, 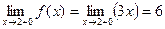 .
. , т.е. в точке х=2 функция имеет разрыв 1-го рода и непрерывна слева.
, т.е. в точке х=2 функция имеет разрыв 1-го рода и непрерывна слева.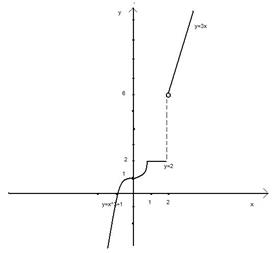 рис.2
рис.2 .
.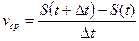 . Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть
. Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть 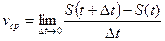 .
.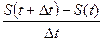 называется разностным отношением, а его предел
называется разностным отношением, а его предел 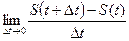 - производной функции S(t) и обозначается S/(t).
- производной функции S(t) и обозначается S/(t).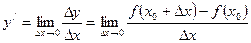 .
.
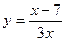 ; в) у=(x4-5x3+7)5
; в) у=(x4-5x3+7)5
 . В нашем случае u= x4-5x3+7
. В нашем случае u= x4-5x3+7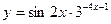 .
.
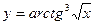 .
.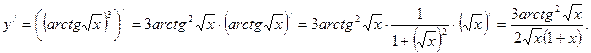
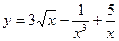 3) y=3x2∙43x.
4)
3) y=3x2∙43x.
4)  5)
5) 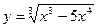 6) y= (x3-4x4+21x)5.
7)
6) y= (x3-4x4+21x)5.
7) 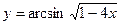 8)
8) 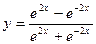
 3)
3)  4)
4) 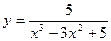 5)
5) 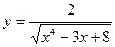 6) y= 2(3x2-x6+5)4.
7)
6) y= 2(3x2-x6+5)4.
7) 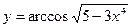 8)
8) 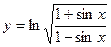
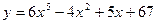 2)
2)  3)
3) 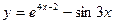 4)
4) 
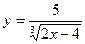 6)
6)  7)
7)  8)
8) 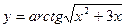
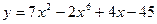 2)
2) 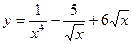 3)
3)  4)
4) 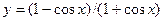 5)
5)  6)
6) 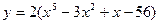 7)
7) 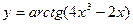 8)
8) 
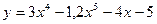 2)
2) 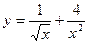 3)
3) 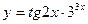 4)
4) 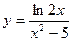 5)
5) 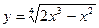 6)
6) 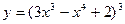 7)
7) 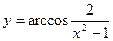 8)
8) 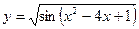
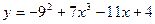 2)
2)  3)
3) 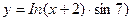 4)
4)  5) y=
5) y= 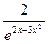 .
6)
.
6) 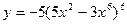 7)
7) 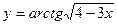 8)
8) 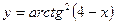 .
.
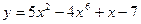 2)
2)  3)
3) 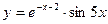 4)
4)  5)
5) 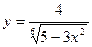 6)
6) 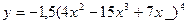 7)
7)  8)
8) 
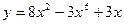 2)
2) 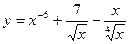 3)
3) 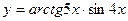 4)
4) 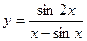 5)
5)  6)
6)  7)
7) 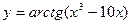 8)
8) 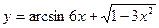
 2)
2) 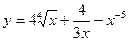 3)
3)  4)
4) 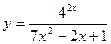 5)
5)  6)
6) 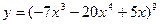
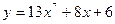 2)
2)  3)
3) 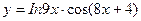 4)
4)  5)
5)  .
6)
.
6) 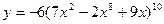
 8)
8) 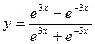 .
.
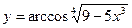 8)
8) 
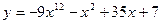 2)
2) 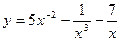 3)
3) 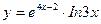 4)
4)  5)
5)  6)
6) 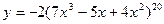 7)
7)  8)
8) 
 2)
2) 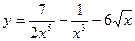 3)
3) 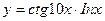 4)
4)  5)
5) 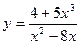 6)
6)  7)
7)  8)
8) 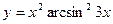
 2)
2) 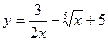 3)
3)  4)
4) 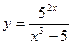 5)
5)  6)
6) 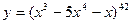 7)
7) 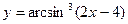 8)
8) 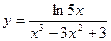
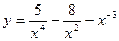 3) y=e5x∙sin(x-5).
4)
3) y=e5x∙sin(x-5).
4) 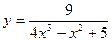 5)
5) 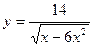 6) y= -5,5(9x2-7x6+1)14.
6) y= -5,5(9x2-7x6+1)14. 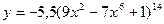 7)
7)  8)
8) 

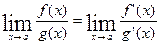
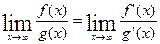
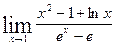
 ; g¢(x) = ex;
; g¢(x) = ex;
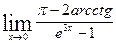
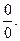
 ;
; 
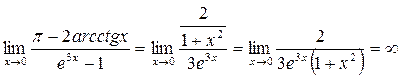

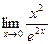
 ,
, 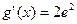 .
.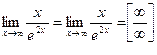
 ,
, 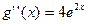 , тогда имеем:
, тогда имеем: 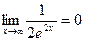
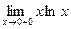
 . Для решения и таких пределов можно применить правило Лопиталя, предварительно сведя ее к неопределенности
. Для решения и таких пределов можно применить правило Лопиталя, предварительно сведя ее к неопределенности 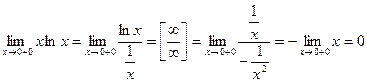
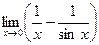
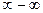 . И здесь можно применит правило Лопиталя, сведя ее к виду
. И здесь можно применит правило Лопиталя, сведя ее к виду 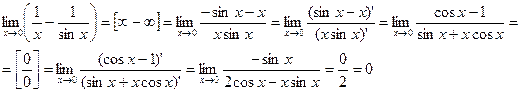
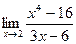 2.
2. 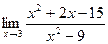 3.
3. 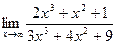 4.
4. 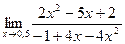
 5.
5.  6.
6. 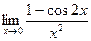 7.
7. 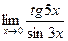 8.
8. 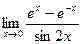 9.
9.  10.
10. 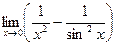
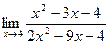 2.
2.  3.
3. 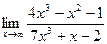 4.
4. 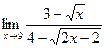 5.
5.  6.
6. 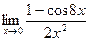 7.
7.  8.
8. 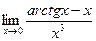 9.
9. 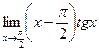 10.
10. 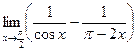
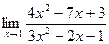 2.
2.  3.
3. 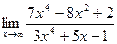 4.
4. 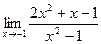 5.
5.  6.
6.  7.
7. 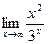 8.
8.  9.
9.  10.
10. 
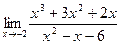 2.
2.  3.
3.  4.
4. 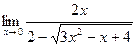 5.
5. 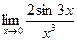 6.
6. 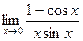 7.
7. 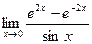 8.
8. 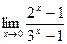 9.
9. 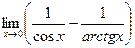 10.
10. 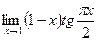
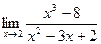 2.
2. 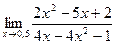 3.
3. 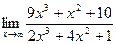 4.
4. 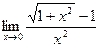 5.
5.  6.
6. 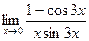 7.
7. 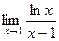 8.
8. 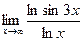 9.
9.  10.
10. 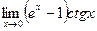
 2.
2. 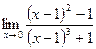 3.
3.  4.
4.  5.
5. 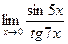 6.
6. 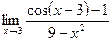 7.
7.  8.
8. 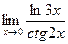 9.
9.  10.
10. 
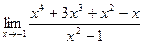 ;
2.
;
2. 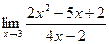 ;
3.
;
3. 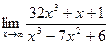 ;
4.
;
4.  5.
5. 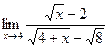 ;
6.
;
6.  ;
7.
;
7. 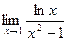 ;
8.
;
8. 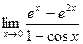 ;
9.
;
9. 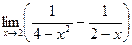 ;
10.
;
10. 
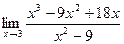 .
2.
.
2.  ;
3.
;
3. 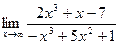 ;
4.
;
4.  ;
6.
;
6. 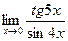 7.
7.  ;
8.
;
8. 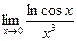 ;
9.
;
9.  ;
10.
;
10. 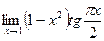
 .
2.
.
2. 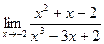 ;
3.
;
3.  ;
4.
;
4.  ;
5.
;
5.  ;
7.
;
7.  8.
8. 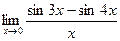 ;
9.
;
9. 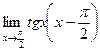 10.
10. 
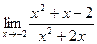 .
2.
.
2. 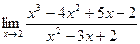 3.
3. 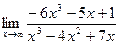 4.
4. 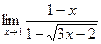 5.
5.  6.
6. 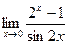 7.
7. 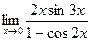 8.
8. 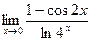 ;
9.
;
9. 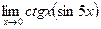 ;
10.
;
10. 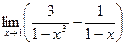
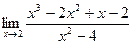 .
2.
.
2. 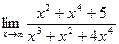 4.
4.  5.
5. 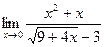 ;
6.
;
6. 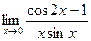 7.
7. 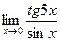 8.
8.  ;
9.
;
9. 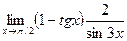 10.
10. 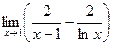
 .
2.
.
2. 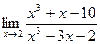 3.
3. 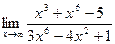 4.
4. 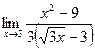 ;
5.
;
5. 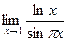 6.
6.  7.
7. 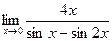 8.
8. 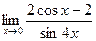 ;
9.
;
9. 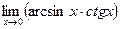 10.
10. 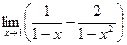
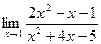 .
2.
.
2. 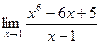 3.
3. 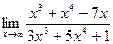 4.
4. 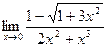 ;
5.
;
5. 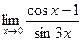 ;
6.
;
6. 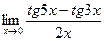 ;
7.
;
7. 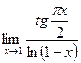 ;
8.
;
8. 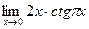 9.
9. 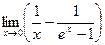 ;
10.
;
10. 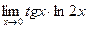
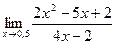 .
2.
.
2.  3.
3.  4.
4. 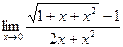 5.
5. 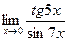 ;
6.
;
6. 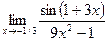 ;
7.
;
7. 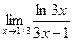 ;
8.
;
8. 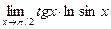 ;
9.
;
9.  ;
10.
;
10. 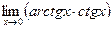

 , где a®0, при Dх®0.
, где a®0, при Dх®0. .
.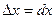 . Поэтому принято вместо
. Поэтому принято вместо 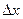 писать dx.. При этом формула дифференциала функции принимает вид:
писать dx.. При этом формула дифференциала функции принимает вид:
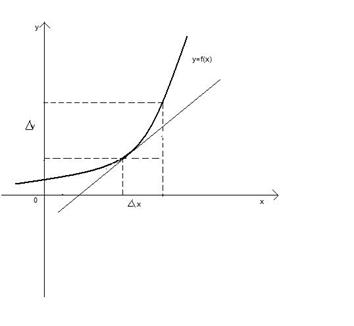


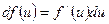 где
где 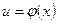 .
. , приращение функции
, приращение функции 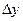 приближённо равно ее дифференциалу, т.е. ∆y»dy, откуда
приближённо равно ее дифференциалу, т.е. ∆y»dy, откуда
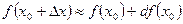 (2)
(2)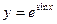 ; б)
; б) 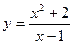 ;
;



