
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства тригонометрических функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
297. Найти области определения функций: 1) у= 1/sin х; 2) у= = 1/(1 — cos jc); 3) j=tg4x; 4) ^=l/ctgx. О 1) sin*#0, хФтск; 2) 1— cosx#0, cosx#l, хФ2пк; 2 4хФп/2+пк, хфп/8 + пк/4; 4) ctg*#0, хФк/2 + пк, кроме того, хфпк, следовательно, хфпк/2. # 298. При каких значениях аргумента принимают наибольшее и наименьшее значения функции: 1) >>=2 sin Зх; 2) ^ = (1/2) cos 2x1 О 1) Имеем sin3*=l, Зх=п/2-\-2пк, значит, при х=п/6+2пк/3 функция принимает наибольшее значение, равное 2. Аналогично, sin3x= — 1, Зх= —тс/2 + 2пк, т. е. при х= — п/6 + 2пк/3, функция принимает наименьшее значение, равное —2. 2) Имеем cos2x= 1, 2х=2пк т. е. при х=кк функция принимает наибольшее значение, равное 1/2. Аналогично, cos 2х = — 1, 2х=п(2к+1), т. е. при х=(к/2)(2к+1) функция принимает наименьшее значение, равное -1/2. • 299. Найдите области определения функций: 1) у = 1/sin л:2; 2) у= = tgx/sinx; 3) у=sinx/tgx; 4) у=ctg3x; 5) у=(\ + sinx)/cosx. 300. Найдите области определения функций: 1) ^=tgxctgx; }> = cosx+ctgx; 3) у= 1 / (sin х+cosx); 4) у= 1 /(sin2x—sinx); 5) }> = ctgx/(sinx—cosx). 301. При каких значениях аргумента принимают наибольшее и наимецьшее значения следующие функции: 1) jy=sin (х— 1); 2) у = = cos(tc/4+x); 3) }>=3sin4x; 4) j; = (l/2)cos5x? 302. Найдите множества значений функций: 1) ^=sin|x|; 2) у= = |sinx|; 3) >>=cos|x|; 4) }> = |cosx|. 303. В каких границах могут изменяться функции: 1) у= 1—sinx; j = 3 + sinx; 3) у= 2— cosx; 4) }>=5+cosx? 304.Имеют ли наибольшее и наименьшее значения функции: 1) y=tgx; 2)y=|tg*|; 3) y=tg2x? 305. Найдите наибольшее и наименьшее значения функций: 1) j;=4 + sin(x— я/12);.2) у = 6 — sin2x; 3) ^ = 5 — 3|sinx|. 306. Найдите множества значений функций: 1) j;=sin х+cosx; 2) j; = 3sinx+4/3cosx; 3) }> = sinx—^/зcosx (см. задачу 235). 307. Исследуйте с помощью производной и сформулируйте основные свойства функций: j; = sinx, у = cosx, y = tgx, y = ctgx. § 29. ПОСТРОЕНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 308. Построить графики функций: 1) >> =,4sinx; 2) j=sin(x+a); 3) ^=sina)x. О 1) Если А>0, то данная функция имеет те же промежутки возрастания и убывания, что и sinx, наибольшее значение функции равно А, а наименьшее равно —А. График получается растяжением синусоиды >>=sinx в А раз от оси абсцисс. Такое преобразование называется преобразованием амплитуды. На рис. 60 изображены графики функций >>=sinx, у=2sinx, >>=(1/2)sinx. 2)
из графика функции у=sinx параллельным переносом начала координат в точку ос; 0). Такое преобразование называется сдвигом фазы. На рис. 61 изображен график функции;; = sin(x—я/4). 3) Наибольшее значение этой функции равно 1, а наименьшее равно — 1; период равен 2 тс/со. Полагая со= 1, ю=2 и со = 1/2, построим графики функций y=sinx, >>=sin2x и >>=sin(x/2). График функции у = sin2x (период Т—п) может быть получен путем «сжатия» синусоиды у = sinx вдоль оси абсцисс в два раза. Аналогично, график функции >>=sin(х/2) (период Т=4п) может быть получен путем «растяжения» синусоиды у=sinx вдоль оси абсцисс в два раза. Такое преобразование называется преобразованием периода. Графики изображены на рис. 62. ф
309. Построить графики функций:
О 1) Преобразуем данную функцию следующим образом: у=sin х 4- cos х=у/2 sin (х 4- п/4). График изображен на рис. 63. 2) Запишем данную функцию в виде у=cos2 х=(1 /2) (1 + cos 2х). Последовательность построения графика видна на рис. 64. ф Постройте графики функций: 310. 1) >>=3sinx; 2) j; = 2cosx; 3) j>=(— l/3)sinx. 311. 1) >>=sin(x—я/6); 2) у=cos(x4-я/3); 3) y=tg(x—я/4). 312. 1) у—cos2x; 2) y=cos(x/3); 3) >> = tg(x/2). 313. 1) y=sinx—cosx; 2) j; = sin2x. § 30. СМЕШАННЫЕ ЗАДАЧИ 314. Открытый желоб в сечении имеет форму равнобедренной трапеции (рис. 65), основание и боковые стороны которой равны а. Чему равен угол наклона а стенки желоба к его высоте, проведенной из вершины тупого угла, при наибольшей пропускной способности желоба? Найдите производные следующих функций: 315. 1) 7 = (l/3)sin3x—sinx; 2) j; = cos(x4-tf)sin(x—a). 316. 1) y= —; 2) y=tg2x—ctg2x; 3) j>=tg22x+ctg22x. tg Зх— 1 317. 1) y=lnctgx; 2) /(x) = lnsin(x/3); вычислите /'(я/2); 3) y= = In cos2 X. 318. 1) v = ln / ~^C0S*; 2) v = lnsin2(x— 1); 3) w=lntg2z2. yj 1 — COS X 319. 1) s = \nesin2t; 2) j; = esinxcosx; 3) >>=etgxcos2x. 320. 1) y=SLTCCOSy/\— x2; 2) w=arcctg-j-^; 3) j;=arctg4/x4- + arcctg yfx. ! gx _ с ~ x / " 321. 1) j;=arccos>/l— e2x\ 2) y= arcsin^^^; 3) y = SLrctgy/ex— 1. ЗАЧЕТНАЯ РАБОТА вариант II вариант Вычислите производные при за- Вычислите производные при за данных значениях аргумента: данных значениях аргумента: 1) /(x)=sin2lnex, /(0); 1) /(.*)=In tg2 2х, /(я/8); 2) f(x)=3 In у/ cos 2х, /' (я/8); 2) /(*)=2 In yiin~2x, /' (я/8); 3) f(x)=arccos y/x, /'(1/2); 4) /(*) = 8 sin2* cos л:, /'(я/4). 5) Точка движется прямолинейно по закону s=sin2/. Найдите момент времени t, когда ее ускорение равно 1. 3) /(*)=arctg е *, /'(0); 4) /(x)=sin2jc(l+cos2x),/'(я/4). 5) Точка движется прямолинейно по закону 5=sin2/. Найдите момент времени /, когда ее ускорение равно нулю.
Глава 10 ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ § 1. ВЫЧИСЛЕНИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ Дифференциалом функции y=f(x) (или дифференциалом первого порядка) называется произведение производной этой функции /'(*) на произвольное приращение аргумента Ajc: dy=f'(x) Ах. Дифференциал аргумента равен приращению аргумента: dx — Ах. Поэтому дифференциал функции равен произведению ее производной на дифференциал аргумента: dy=f'(x)dx. (10.1) Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка: d2y=f"(x)dx 2, (10.2) т. е. дифференциал второго порядка функции y=f(x) равен произведению второй производной этой функции на квадрат дифференциала аргумента. 1. Найти дифференциалы первого порядка следующих функций: 1) у=(х3-2)4; 2) у=у/х2-1; 3) ^lnsin^*. О Воспользуемся соотношением (10.1): 1) dy=((x3 — 2)*)'dx=4(x3—2)3 • 3x2dx=\2x2(x3 — 2)3 dx; 2) dy=(In sin у/х)'dx= —cosVx-— ^—dx =^ ф sin yfx 2 yfx 2 y/x 2. Найти дифференциалы второго порядка следующих функций: 1) у =In sin2 2х; 2) у = е~х. О Воспользуемся соотношением (10.2): 1 1 8 у'——^—-2sin2xcos2A:-2=4ctg2x; у" = —4 •., ■ -2=—.; sin2 2* sin2 2х sm 2х »2 пА 2 МХ2 1 2 d у—у dx — — -r^rr-dx, sin^ 2х 1) у'=—е х; у"— е х\ d2y=y"dx2 = e Xdx2. ф 3. Найдите дифференциалы первого порядка следующих функ- ций: 1)>>=(1-х2)5; 2) у=(ах2 + Ь)г; 3) y=s/4-2x1\ 4) y=l/y/2x-l; j=lncos2x; 6) j;=ln(l/N/x); 7) j>=arccos;*:2; 8) y=arcctg(l/x). 4. Найдите дифференциалы второго порядка следующих функций: 1) у = lncos2*; 2) у = \ntg2x; 3) у=аЪх\ 4) j> = arccosx; 5) у= = arctgx2. § 2. АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ Рассмотрим функцию у=/(х). Предположим, что величина х получена непосредственным измерением или в результате приближенного вычисления. Тогда при нахождении величины х мы допускаем не зависящую от нас погрешность А*. Пусть х—приближенное значение аргумента (измеряемой величины), Ах—абсолютная погрешность величины х,---------- относительная погрешность л; величины х, а х+Ах—истинное значение измеряемой величины (Ад: может быть как положительным, так и отрицательным числом). Тогда х определяет приближенное значение функции /(х), а х+Ах—ее истинное значение /(х+Ах), откуда следует, что абсолютная погрешность функции 1I = 1/(х +Ах)—/(х) |. При малых значениях Ах (близких к нулю) величину Ау можно приближенно заменить дифференциалом dy: Ay=f(x+Ax)—f(x)&f'(x)dx=dy. Выгода замены приращения функции Ау ее дифференциалом dy состоит в том, что dy зависит от Ах линейно, а Ау представляет собой обычно более сложную зависимость от Ах. Полагая Ay&dy, получим выражение для относительной погрешности 8 величины у:
5. Сравнить относительные погрешности при вычислении площади круга радиуса г=125см, считая, что абсолютная погрешность равна: 1) приращению площади круга; 2) дифференциалу площади круга. О 1) Находим приращение AS площади круга и относительную № 2 ^ погрешность — при вычислении площади круга S=nrz. Будем считать, что S погрешность при измерении радиуса не превышает +0,5 см. Имеем A.S=7i(r+Ar)2 —71г2 = я(2гАг+(Аг2))=я(2 • 125 *0,5+0,25)= 125,25л; AS 125,25л —=------ ^=0,008016*0,8%. S 71 • 125 dS 2) Найдем дифференциал dS и относительную погрешность — при S вычислении площади круга: dS 2nrAr dr dS=2nrAr=2n • 125 *0,5= 125л; —=---------- =-=2 ■—. S nr2 г Значит, относительная погрешность при вычислении площади круга равна удвоенной относительной погрешности, полученной при измерении радиуса: dS dr 0,5 Т 7 Тй Итак, видим, что во втором случае вычисление было значительно проще и выполнено без ущерба для точности вычисления. Определим относительную погрешность приближения при замене приращения AS дифференциалом dS: AS-dS 0,25 к AS—dS= 125,25л -125тс=0,25л:; ———==0,002 = 0,2%. dS 125те Относительная погрешность приближения составила всего 0,2%. ф 6. Найдите относительную погрешность при вычислении длины окружности, если г = 50 см, Дг = 0,5 см. 7. Найдите относительную погрешность при вычислении величины, заданной уравнением у=х3, если х — 2 и Ах=0,01. § 3. ВЫЧИСЛЕНИЕ ПРИБЛИЖЕННОГО ЧИСЛОВОГО ЗНАЧЕНИЯ ФУНКЦИИ Пусть дана функция y=f(x); приращение этой функции Ay=f(x+Ax)— —/(jc), ее дифференциал dy=f'(x)dx. При достаточно малых (близких к нулю) приращениях аргумента Ах будем считать, что Ay&dy, т. е. что приращение функции приближенно равно ее дифференциалу. Заменив приращение функции ее дифференциалом, получим /' (х) dx «/(х+Ах) —/(х), откуда /(х+Ах)«/(х)+/'(х)Ах. (10.3) Применение этой формулы дает значительное упрощение вычисления числового значения функции; геометрически это соответствует замене участка кривой отрезком касательной. 8. Найти приближенное значение приращения функции у= = 2jc 3 + 5 при х = 2 и Ад: = 0,001. О Имеем Ay&dy = 6x2dx=6 *22 0,001 =0,024. Точное значение приращения А_у = 2 (х+Ах)3 + 5 — 2х 3 — 5 = 6х 2 Ах+6х (Ах)2 + 2 (Ах)3 = = 6 • 4 • 0,001 + 6 • 2 • 0,000001 + 2 • 0,000000001 =0,024012002. ф 9. На сколько увеличится при нагревании объем шара радиуса R, если его радиус удлинился на величину АЛ? О Объем шара вычисляется по формуле V=(4/3)тс/?3. Считая приращение AR аргумента R малым, заменим приращение объема шара его дифференциалом: AV&dV. Следовательно, для вычисления приращения объема шара достаточно найти дифференциал функции K=(4/3)tlK3, т. е. dV=4nR2dR. • 10. Найти приближенное значение функции /(jc) = 5jc3 —2х+3 при х = 2,01. О Полагая х=2 и Ах = 0,01, получим /(х)=/(2)=5 *23 —2 *2+3 = 39; /' (х)Ах=/ (2) * 0,01 = (5х3 —2х+3)'Ах=(15х2 —2)Ах=(15 *22—2)0,01 =0,58. По формуле (10.3) находим /(2,01) = 39+0,58 = 39,58. Найдем точное значение функции: /(2,01) = 5 • (2,01)3—2*2,01 +3 = = 39,583005. • 11. Найдите приближенные значения приращений функций: у=Зх2 + 5х+1 при х = 3 и Ах = 0,001; 2) у=хъ +х— 1 при х—2 и Ах = 0,01; 3) у=\пх при 10 и Ах = 0,01. 12. На сколько увеличится при нагревании объем куба с ребром 10 см, если удлинение ребра равно 0,02 см? 13. Найдите приближенные значения функций: 1) /(х) = 2х2 — —х+1 при х = 2,01; 2) /(х)=х2 + Зх+1 при х=3,02; 3) /(*) = = (1/3)х3+(1/2)х2 —2х+4 при х= 1,1. § 4. ФОРМУЛЫ ДЛЯ ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЙ Применяя формулу (10.3), легко получить различные формулы для нахождения приближенных числовых значений. Ниже рассмотрим формулы, имеющие практическое значение в приближенных вычислениях. Формула для приближенного вычисления степеней:
Частные случаи формулы (10.4): 1) п — 2, (х + Ах)2«х2 + 2хАх; 2) п — 3, (х+Ах)3«х3 + Зх2Ах; 3) jc= 1, (1 +Ах)"«1 +пАх. Формула для приближенного вычисления корней:
пухп 1 Частные случаи формулы (10.5): п — 2, у/х+Ах&у/х+ Х 1
^/1+Дх«1+—. п Формула для приближенного вычисления обратных величин:
1 Формулы для приближенного вычисления синусов и тангенсов малых углов: sin Ах* Ах; tgAx*Ax. 14. Найти приближенные значения: 1) (4,012)2; 2) УйООб; 1/1,004. О 1) Полагая в соотношении (10.4) х=4, Ах=0,012, получим (4,012)2 = =(4+0,012)2*42+2-4 0,012=16,096*16,1 (точный ответ 16,096144) 1) Полагая в соотношении (10.5) х=1, Ах=0,006, получим у/1,006 = =,/1+0,006* 1+0,006/2= 1,003. 2) Полагая в соотношении (10.6) х=1, Ах = 0,004, получим 1/(1+0,004) = = 1-0,004 = 0,996. ф 15. Вычислить sin 12'. О Так как 12'=0,0035 рад, то sin 0,0035=0,0035. По таблице натуральных значений синуса находим sin 12'= 0,0035. ф 16. Найдите приближенные значения степеней: 1) (9,Об)2; 2) (1,012)3; 2) (9,95)3; 4) (1,005)10; 5) (0,975)4. 17. Найдите приближенные значения корней: 1) \/1,012; 1) У25Л6; 3) У^84; 4) /КН; 5) ^9^5; 6) i°/W 18. Найдите приближенные значеййя величин: 1) 1/0,99; 2) 1/9,93; 2) 1/(1,004)2. 19. Вычислите: 1) sin42'; 2) sin2°06', 3) tgl°12'; 4) tg3°18'. § 5. ВЫЧИСЛЕНИЯ ПО СПОСОБУ СТРОГОГО УЧЕТА ПОГРЕШНОСТЕЙ При вычислениях нередко возникает необходимость знать границы допущенной погрешности промежуточных вычислений и окончательного результата. Такой способ ведения приближенных вычислений называется способом строгого учета погрешностей. Для этого необходимо знать, как вычисляются границы относительных погрешностей алгебраической суммы, произведения, степени, корня и частного. 20. Доказать, что относительная погрешность произведения не превышает суммы относительных погрешностей ее сомножителей.
In y = lnw + lnt;; — У Так как абсолютная величина суммы не превышает суммы абсолютных величин слагаемых:
то
21. Доказать, что относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя. О Пусть дана функция y=u/v, где u=f(x) и u = (p(jc). Прологарифмировав и взяв дифференциал от функции y=u/v, получим dy du dv \ny = \nu—\nv, —=------------. у и V
22. Доказать, что относительная погрешность степени равна относительной погрешности основания, умноженной на показатель степени. О Пусть дана функция у=хп. Прологарифмируем ее и найдем дифференциал: dy dx ту=птх; — =п —. у х / \ ^х Относительная погрешность равна е(лг")=л—. Частные случаи: 1) я = 2, е(х2)=2—; 2) л = 3; е(д:3)=3—. • х х 23. Доказать, что относительная погрешность корня равна относительной погрешности подкоренного числа, деленной на показатель степени корня. О Пусть дана функция у = \[х. Прологарифмируем ее и найдем дифференциал: 1 dy 1 dx ln^=-ln jc; —=---------. n у n x Относительная погрешность равна s(^/x)=^ Частные случаи: 1) п = 2, 6^/*)=^ —; 2) л = 3, е(1/х)=\—. ф х 3 х 24. Найти относительную погрешность числа х при вычислении этого числа по его логарифму у = lgx. О Пусть lg* был вычислен с погрешностью Ау, тогда при нахождении по нему числа х будет допущена погрешность Ajc. Относительная погрешность числа jc равна —.Так как абсолютная погрешность логарифма х Ах Ау& 0,4343—, то х Ах Ау х 0,4343 Таким образом, относительная погрешность числа л: при вычислении его по его логарифму не зависит от значения числа х, а зависит только от погрешности, с которой был найден логарифм числа х. ф 25. Найти относительную погрешность точности отсчета на логарифмической линейке со шкалой 250 мм. О Допустим, что при установке визира или отсчета со шкалы наибольшая погрешность составляет 0,1 мм. Найдем абсолютную погрешность логарифма числа. Вся шкала логарифмической линейки длиной 250 мм соответствует числу, логарифм которого равен единице (lg 10 = 1). Следовательно, на 0,1 мм шкалы абсолютная погрешность логарифма числа будет в 250 раз меньше, т. е. Ajc А}> = 0,1/250 = 0,004. Так как Ау = 0,4343—, то Ал: Ау 0,004 х 0,4343 0,4343 т. е. относительная погрешность точности отсчета составляет 0,1% (в любой части шкалы), ф 26. При измерении прямоугольного поля нашли его длину и = 60 м и ширину v = 23 м. Погрешность при измерении длины не превышает 0,3 м, а при измерении ширины 0,2 м. Определить границы погрешности, которую мы допускаем, принимая площадь прямоугольника равной 60 *23 = 1380 м2, и относительную погрешность, допущенную при вычислении площади. О Имеем \du\<0,3, |*Л;|<0,2. При наихудших условиях |*й/| = 0,3, \dv\ = 0,2. Найдем абсолютную погрешность произведения: d(uv) = vdu+udv = 23 • 0,3 + 60 * 0,2 = 18,9 * 19 (м2).
Относительную погрешность вычислим по формуле е(ш?) = , ч 0,3 0,2 1 2 v ; 60 23 200 230 Итак, относительная погрешность не превышает 1,4%. ф 27. Для нахождения плотности тела определены его масса mt= 484 г и масса вытесненной им воды т2 = 62 г. Абсолютные погрешности Атх =0,5 г и А/и2 = 0,4г. Найти относительную погрешность при вычислении плотности тела.
=^^ «0,00103 +0,00645=0,00748 «0,7%. • 28. Найти относительную погрешность, допущенную при измерении объема куба, если ребро равно 12,5 см. Абсолютная погрешность Ах = 0,05 см. О Полагая dx=0,05 см, имеем Ф>з^=з,^^0,012=1,2%.. 29. Найти относительную погрешность, допущенную при вычислении длины стороны квадрата, если площадь квадрата равна 37,7 см2. Абсолютная погрешность Ад:=0,05 см. О Обозначив длину стороны квадрата через у и площадь через f х, получим: у=у/х=у/37,1 dx=0,05; , >----- ч 1 0,05 0,05 е(Уз7/7)=-000663 *0,1%. • 30. При измерении площади параллелограмма нашли его основание а=70 см (Да = 0,4 см) и высоту h = 48 см (АЛ = 0,3 см). Определите относительную погрешность, допущенную при вычислении площади параллелограмма. 31. Даны два приближенных числа 82,6 и 64,8. Найдите относительную погрешность их частного. 32. Найдите относительную погрешность, допущенную при измерении площади квадратной комнаты, если взято округленное значение стороны, равное 6,4 м (абсолютную погрешность принять равной 0,05 м). 33. Найдите относительную погрешность, допускаемую при вычислении длины стороны квадрата, если площадь квадрата равна 68,5 см2. § 6. СМЕШАННЫЕ ЗАДАЧИ 34. Найдите дифференциалы первого порядка следующих функций: 1) у = ех sinx; 2) у = ахех; 3) y^ex-Jlx\ 4) у=(ех-е *)[18]; 5) У=-р—}\ 6) У=-^г- 35. Вычислите приближенные значения приращенйй функции: 1) у—sin2д: при х=к/6 и Дл:=0,02; 2) у = 1пх2 при х = 20 и Дх=0,01; 3) j = arcsinx при х = у/з/2 и Дх=0,02. 36. Вычислите приближенные значения функций: 1) f(x) = x[19] + +x2+x+l при х = 0,001; 2) f (х) = х*—\ при х= — 3,3; 3) /(*) = = х/ч/х[20] + 3 при jc= 1,1. 37. Найдите относительную погрешность при вычислении величины, заданной уравнением: 1) у=х2 при х=10 и Дл: = 0,01; 2) у = х3 при х = 3 и Дх=0,02. 38. Составьте формулы для вычисления относительных погрешностей функций: 1) у = sin23x; 2) y=tg2x. 39. Составьте формулы для вычисления относительных погрешностей функций: 1) y = esin2x; 2) у = Зу/х. ЗАЧЕТНАЯ РАБОТА
I вариант 1) Вычислите дифференциал функции >>=lncos[21]x при х=п/4 и </х=0,01. 2) Вычислите относительную погрешность функции F=(4/3)nR3 при Я=300 и dR=0,3. 3) Найдите приближенное значение приращения функции у — хъ—х2 при х=2 и Ах=0,01. 4) Найдите приближенное значение функции/(лг)=лг3 — лг2-Ьлг—3 при x=3,03. 5) Вычислите приближенное значение величины 1/0,998. II вариант 1) Вычислите дифференциал функции jh=In tg 2хг при jc=7с/8 и dx—0,03. 2) Вычислите относительную погрешность функции у=х3 при х=750 и dx=0,5. 3) Найдите приближенное значение приращения функции у=2^/х +4 при х = 25 и Ал: = 0,01. 4) Найдите приближенное значение функции f(x) = Зх[22]—х2 + 5х—1 при jc=3,02. 5) Вычислите приближенное значение величины (1,02)[23].
Глава 11 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ )
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1000; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |


 График данной функции получается
График данной функции получается Рис. 61
Рис. 61
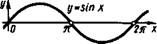

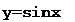

 1) j^sinx+cosx; 2) y=cos2x.
1) j^sinx+cosx; 2) y=cos2x.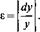
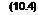 (х+Ах)"«х"+ях" 1Ах.
(х+Ах)"«х"+ях" 1Ах.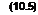 \/ х+Ах&п/х-\ ---------..
\/ х+Ах&п/х-\ ---------..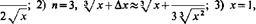
 _!_~1 Ах х+Ах х х2
_!_~1 Ах х+Ах х х2 1—Ах; 3) х = 1 и Ах<0,
1—Ах; 3) х = 1 и Ах<0,
 + Ах.
+ Ах. О Пусть дана функция y=uv, где м=/(х) и t? = <p(x). Прологарифмируем ее и найдем дифференциал:
О Пусть дана функция y=uv, где м=/(х) и t? = <p(x). Прологарифмируем ее и найдем дифференциал: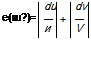
 Это наибольшая величина абсолютной погрешности, которую мы можем допустить, принимая площадь участка равной 1380 м2. Округляя погрешность в сторону увеличения и принимая ее равной 20 м2, найдем границы погрешности при вычислении площади. Таким образом, площадь не превосходит 13804-20= 1400 (м2) и не менее 1380—20= 1360 (м2).
Это наибольшая величина абсолютной погрешности, которую мы можем допустить, принимая площадь участка равной 1380 м2. Округляя погрешность в сторону увеличения и принимая ее равной 20 м2, найдем границы погрешности при вычислении площади. Таким образом, площадь не превосходит 13804-20= 1400 (м2) и не менее 1380—20= 1360 (м2).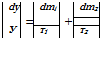 О Так как у=т1/т2, то
О Так как у=т1/т2, то


