
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подставив это выражение во внешний интеграл, получим 6Содержание книги
Поиск на нашем сайте {(Здс+т)^=[х+т"1=78- Теперь вычислим двойной интеграл по формуле (29.6): Я (.x+y)dxdy=[dy\ (дс+^) dx. D 12 Найдем внутренний интеграл: J*(jc+^)<fcc=|^y+jc>'J =( 18 + 67 )—(2+2у)=4у+16. Далее найдем внешний интеграл: 1 (4у +16) dy=[2у2 +167] ^=78, Т. е. получили тот же ответ, ф 18. Вычислить двойной интеграл jj (х2 —y)dxdy по облас- D ти D, заданной системой неравенств 0<х^3; (рис. 204). О Область D является простой как относительно оси Ох, так и относительно оси Оу; поэтому вычислим этот интеграл двумя способами. Произведем вычисление по формуле (29.7). Пределами внутреннего интеграла являются функции у=х2 и у=9, составляющие уравнения нижней и верхней границ области D, а пределами внешнего интеграла являются абсциссы jc=0 и х=3. Значит, tf(x2-y)dxdy=]dx](x2-y)dy D 0 X2 Вычислим внутренний интеграл по переменной у в предположении, что х—постоянная: \{x‘-y)dy-[x‘yJl\-
/ 81\ / A 1 81 = (9x2—— J—I x4—— J = 9x2—-x4 ——. Вычислим внешний интеграл: =-64,8. Произведем теперь вычисление по формуле (29.8). В этом случае область D выражается системой неравенств 0<^^9, 0 ^ л: ^^/у, т. е. пределами внутреннего интеграла служат функции х=0 и х=у/у, а пределами внешнего интеграла—ординаты у=0 и у=9. Поэтому 9 у/у 9 9 jj(x2~y)dxdy=jdy j*(x2-j)^=J*^Y-^J dy=^^ym—y 3/2 ^jdy= D ООО О 2 Г 2 2 I9 = -\\yV2dy=-r-ybl21 = —64,8. • 3 19. Вычислить двойной интеграл JJ-rfjcrfv по области D, D заданной линиями х=1, х=4, у=х и у = 2у/х. О Находим точки пересечения этих линий: Г*=1; Гх=4, ij>=2<s/x, М(\\2)\Ху=2у/х, N(4;- ; 4) (рис. 205). Область D определяется системой неравенств К* <4, Вычислим двойной интеграл по области D: 4 2 VЗс 4 _ 4 20. Вычислить двойной интеграл jj (x+2y)dxdy по области D, D А 4 ограниченной линиями у=х, у=4х и у=~. О Находим точки пересечения этих линий: у=х, у=~, М(2; 2); 1 у=-, N(1; 4) (рис. 206). Область D разобьем на две области D1 и D2, которые соответственно определяются системами неравенств 0<х<1, х^у^4х и 1 ^х^2, х^у^4/х. Вычислим двойной интеграл по области Dt: Х 1 I1=^(x + 2y)dxdy = ^dx^(x + 2y)dy = ^\xy+y2Yxxdx=
1
О о Вычислим двойной интеграл по области D2: Ах 2 /2 = Q(x+2y)dxdy =Jrfx ^(x + 2y)dy=^[ху+у2]** dx= D2 1 x 1 1 2 = x2—x2^dx=J(4+ 16x-2—2x2)dx=j^4x———^x3 J =7^. l l Значит, /=/1+/2 = 6+7^=13^. # 21. Изменить порядок интегрирования в двойном интеграле \dx Xj 2f(x,y)dy. О х О Зная пределы интегрирования, запишем область интегрирования D в виде системы неравенств O^x^l, х2 + 2. Построим линии х=0, х= 1, у=х и у=— х2 + 2 (рис. 207). Найдем точку пересечения линий: s Л ч \у=-х2 + 2, М(\;\). Область D является простой относительно оси Ох. Рассмотрим область D относительно оси Оу. Через точку Af(l; 1), в которой стыкуются участки верхней ^ границы области D, проведем прямую,
' 1 ' О^х^у и \^у^2; О^х^у/2-y. Тогда, согласно формуле (29.8), получим 1 -х 2 + 2 1 У Х=7 Л fdx f f(x,y)dy=\dy\f(x,y)dx+ Ox 0 0 Рис. 207 +[dy j f(x, y)dx. • 1 0 22. Вычислите повторные интегралы: 1) \dx\{x2+y2)dy; 2) $dx](x+2y)dy; 3) \dy\(x2+y2)dx; 1 Ox 10 2 2x 2 4у 1 y2 4) \dx j -dy; S) \dy \ xydx; 6) J dy J (Зле—2 y)dx. 2 Xх 12 у 0 0 23. Вычислите двойные интегралы по областям, ограниченным указанными линиями: 1) JJxdxdy, ху=4, х+у—5=0; 2) \\x2ydxdy, D D х2+у2 = 16, х+у —4 = 0; 3)\\ydxdy, у=х2, х= —2, х=2, у=4; D tytfxtydxdy, у—х, у= l/х, х=2; 5) JJ xydxdy, у= 0, у=4—х2; D D 6) \\x*dxdy, л: = 0, у=х, у = 6—х2. D 24. Вычислите двойные интегралы по областям, ограниченным указанными линиями, предварительно разбив заданную область на две области: 1) \\xdxdy, у=х2, у=2х, у=Зх; 2 ) \\(x+y)dxdy, у=~, у=х, у= 4; D D Х 3 4 3) J \ydxdy, y=jx, у=-х, х>0, у>0, х2+у2=25. D 4 3 25. Измените порядок интегрирования в двойных интегралах: 1) \dx ] fix, y)dy, 2) jdy j f(x, y)dx; 3) fdx f f(x,y)dy; О у 0 x2 3 у 4 s/16-Х2 4) \dy ] f(x,y)dx; 5) J A: f f(x,y)dy. 1/y -4 о ЗАЧЕТНАЯ РАБОТА II 1) Вычислите повторный ин- 2 у2 теграл J dy { (2x+y)dx. -2 О 2) Вычислите двойной интеграл JJ ху dx dy, где D—область, ограни- JJ ^jdxdy, где D—область, огра- D d У ченная параболами у=х2 и х=у2. ниченная линиями у=\/х, у=х
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 *2
*2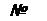 5
5
 1 = J*(4x2 + 16 x2—x2—x2)dx= 18
1 = J*(4x2 + 16 x2—x2—x2)dx= 18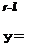
 y=-X +2(x-}f2-y) параллельную оси Ох. Эта прямая делит область D на две области и D2, М(4*л которые запишем в виде систем неравенств
y=-X +2(x-}f2-y) параллельную оси Ох. Эта прямая делит область D на две области и D2, М(4*л которые запишем в виде систем неравенств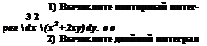 вариант
вариант


