
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы интегрирования. Непосредственное интегрированиеСодержание книги
Поиск на нашем сайте
Совокупность первообразных для функции / (х) или для дифференциала / (х) dx называется неопределенным интегралом и обозначается символом j/ (х) dx. Таким образом, J/ (х) dx=F(x) 4- С, если d [/’(х) 4- С] =/ (х) dx. Здесь / (х)— подынтегральная функция; f(x)dx—подынтегральное выражение; С—произвольная постоянная. Приведем основные свойства неопределенного интеграла. 1°. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная: \dF(x) = F(x)+C. 2°. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: d\f(x)dx=f(x)dx, =/(*)• 3°. Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций: I [/(*) +Ф (*)] dx=if(x) dx+$ Ф М dx- 4°. Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла: J af (х) dx = a$f (х) dx. ■ 5°. Если J f (x)dx=F(x) +С и н=(р (х)— любая известная функция, имеющая непрерывную производную, то \f(u)du=F(u) + С. Основные формулы интегрирования (табличные интегралы)
= arcsin -+C; (11.12)
j—-j=-arctg -+C. (11.13) x+a a a При применении формул (11.3), (11.10) и (11.11) знак абсолютной величины пишется только в тех случаях, когда выражение, стоящее под знаком логарифма, может иметь отрицательное значение. Каждую из формул легко проверить. В результате дифференцирования правой части получается подынтегральное выражение. 2. Непосредственное интегрирование. Непосредственное интегрирование основано на прямом использовании таблицы интегралов. Здесь могут представиться следующие случаи: 1) данный интеграл находится непосредственно по соответствующему табличному интегралу; 2) данный интеграл после применения свойств 3° и 4° приводится к одному или нескольким табличным интегралам; 3) данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 3° и 4° приводится к одному или нескольким табличным интегралам.
Найти следующие интегралы: 1} 2) f6x2dx- 3) $4(x2-x+3)dx; О 1) На основании свойства 4° постоянный множитель 5 выносим за знак интеграла и, используя формулу (11.1), получим 1 5dx=5 $dx=5x+C. 2) Используя свойство 4° и формулу (11.2), получим \6х2dx=6 \x2dx=6 ------------------ \-С=2х3 + С. J J 2+1 Проверка: d(2x3 + C) = 6x2dx. Получили подынтегральное выражение; следовательно, интеграл найден правильно. 3) Используя свойства 3° и 4° и формулы (11.2) и (11.1), имеем х3 х2 4 =4 •——4* — + \2х+С=-х3 — 2х2 + \2х+С. Постоянная интегрирования С равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную (Ci — С2 + Съ = С). 4) |2(3x— \)2dx=j (18x2 — 12x+2) dx= 18 f x2 dx—12 (xdx+2 f dx=6x3 — 6x 2 4" 2x 4" C. 5) J——------ ——dx—j*(x2 + 3x4-4)</x=j*x2</x+3Jxtf£x+4Jd!x=^x34- xx2 + 4x + C. ф i,) J*_4л; 2)If- О Используя формулу (11.2), находим: Г x"4+1 х"3 1 1) \x-*dx=—--=— + С=- —5+С; J -4+1 -3 Злг3 Г /JV Г х~1/2+1 ^ 2) 1^7‘г"“Л‘^ЙТТ’г*,"+с‘2^+с' * LjJS; 2)J^; 3 О 1) По формуле (11.3) находим . 1+С. J х 2) Так как dx=d(l+x), то hx), ТО Г dx f</(l4-x) —— = ————In11 +x 4-С. J 14-x J 14-x 3) Так как xdx=^d(x2+1), то Знак абсолютной величины не пишем, так как при любом значении х выражение х2 + 1>0. # 4. 1) J2 Xdx\ 2) J 2х2xdx; 3) \e~3x2xdx.
2х 2xdx=—~ 4-С. In 2 2) Так как х</х=(1/2)*/(х2), то Г Г 1 if 1 2х2 2х2-1 j **,*- j 2--<^)=- j 7*^).--- +С=— +С. 3) Так как xdx= — (l/6)d(— Зх2), то Je“3x2x<*x= — ^Je_3x2<i(—Зх2)= — ^е-3х2 + С. • 5. 1) J sin (ax+b)dx; 2) jcos(5x—3)dx;3) J tg xdx. О 1) Так как d(ax+b) = adx, то dx=(\/a)d(ax+b). Следовательно,
Ilf 1 sin (ax+b)'-d(ax + b)=- sin (ax+b)d(ax+b) = cos (ax b) +C. 2) 3) Так как sinx^ = — d(cosx), то Г fsinxflfx Г d (cosx) tg х dx= I =— I — — In |cosx| + C. ф J J cos x J cos x 6. „ fj*; 2, f 3) f *; 4) J cos2 у J cos2 x3 J 2 sin2 z J sm2 (. (x2+l)
dy 2 = 5tgy+C. cosz у 2) Так как d(x3)=3x2 dx, to x2dx=-d(x3). Следовательно,
COSAXJ
3) По формуле (11.9) находим
-CtgZ+C. sinz z 2
4) Так как x</x=(l/2)<i(x2+1), то

4) Jcos(2 — 3x)dx; 5) \x2cosx*dx. ix Г cosxdx „ Г sinxdx _ч Г cosxdx * J315ГГГГ’ 2)Jj^ 3>JsTw 23' 11 flcos' v1 2) {cos’ 5*' 3) jcos^tt+f.)1 5)j^- з>Ы=г f 2dx _ч Г du _ч Г dx „ f 3dx Чутз^5 Чу!^; 4) Jyi6^' *»Ji& ®fs& «Й?- § 2. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА Отыскание функции по заданной производной или по дифференциалу— задача неопределенная, так как j/ (х) dx означает множество первообразных функций вида y=F(x) + С, отличающихся друг от друга постоянным слагаемым С; С может принимать любые числовые значения, если на первообразную функцию не наложено никаких начальных условий. Чтобы из множества первообразных функций выделить одну определенную функцию, должны быть заданы начальные условия. Под начальными условиями понимается задание частных значений х и у для первообразной функции y = F(x) 4-С, по которым находится определенное значение С, удовлетворяющее этим начальным условиям. 27. Найти функцию, производная которой у' = 3х2 — 6*4-2. О Имеем У = 3х2 — 6х+2, или —=3х2 —6x4-2, т. е. dy=(3x2 — 6х+2)dx. dx Находим интегралы от левой и правой частей последнего равенства: Jdy=J(3x2 — 6x4-2) dx; <у4-С1=х3 — Зх24-2x4- С2. Полагая С2 —Сх = С, получим у=х3 — Зх2 4-2x4-С. Мы нашли общее выражение функций, имеющих своей производной / = 3х2 — 6x4-2. В дальнейшем при интегрировании подобных выражений постоянную интегрирования будем писать только в правой части, ф 28. Найти функцию, производная которой у' = 2х—3, если при х=2 эта функция принимает значение, равное 6. dy О Имеем у' = 2х—3, или —=2х—3, т. е. dy=(2x—3)dx. Интегрируя обе dx части последнего равенства, находим Jdy=j(2x—3)dx; у=х2 — Зх4-С. Вычислим С при заданных значениях х=2 и у = 6. Подставив в выражение для функции эти значения, получим 6 = 22 — 3-2+С, откуда С= 8. Итак, функция, удовлетворяющая заданным начальным условиям, имеет вид у=х2-Зх+8. ф 29. Найти J (cosx—sinx) dx, если при х=п/2 значение первообразной функции равно 6. О Имеем J (cos х—sin x)dx=f cos xdx—Jsinxdx=sin x+cosx+C. Вычислим С при заданных начальных условиях: 6 = sin (я/2) + cos (я/2) + С, откуда С=5. Следовательно, первообразная функция >>=sinx+cosx+5. ф 30. Найти уравнение кривой, если угловой коэффициент касательной в каждой ее точке (х; у) равен 2х. dy О Согласно условию, к—2х. Известно, что fc=tga=—; следовательно, dy dX —=2х, т. е. dy = 2хdx. Интегрируя, получим idy=(2xdx; у=х2 + С. dx
31. Составить уравнение линии, если угловой коэффициент касательной в любой точке касания равен у/х.
у О Согласно условию, к=~; так как х dy dy у к=—, то —=—, откуда, разделив переменах dx х, dy dx ные, имеем —=—. Интегрируя, находим у х
Произвольную постоянную полагаем равной In С для удобства упрощений. Потенцируя, получим у = Сх—уравнение семейств прямых, проходящих через начало координат, ф 32. Найти уравнение кривой, проходящей через точку А (0; 1), у которой касательная в любой точке кривой имеет угловой коэффициент, равный ординате точки касания. dy dy О Согласно условию, имеем к=—=у, т. е. —=dx. Интегрируя, получим dx у 1п^=х+С. Из начальных условий находим In 1=0+С, т. е. С=0; следовательно, у=ех. ф 33. Найдите функцию: 1) производная которой у' = 4х3 —2х-+3; дифференциал которой dy = (2x + 6)dx. 34. Найдите функцию: 1) производная которой у' = 2х—5, если при х= — 3 эта функция принимает значение, равное 28; 2) обращающуюся в нуль при х = 0, если / = Зх2-4х+5; 3) производная которой у' = 3ех + 2х, если при л:=0 эта функция принимает значение, равное 8. 35. Найдите: 1) J(sinx+3cosx)dx, если при х=я первообразная функция равна 4; 2) J(cosx—ex+2x)dx, если при х = 0 первообразная функция равна 3. 36. Найдите уравнение кривой, если угловой коэффициент касательной в каждой ее точке (х; у) равен: 1) — Зх; 2) х+2. 37. Составьте уравнение кривой, если угловой коэффициент касательной в каждой ее точке равен: 1) — у/х; 2) х/у; 3) —х/у. 38. Найдите уравнение кривой, проходящей через начало координат, если угловой коэффициент касательной в любой точке кривой равен х/3. 39. Найдите уравнение кривой, проходящей через точку М(\; 4), если угловой коэффициент касательной к кривой в каждой ее точке равен Зх2 — 2х. 40. Составьте уравнение кривой, проходящей через точку А(—1; 3), если угловой коэффициент касательной в каждой точке кривой равен утроенному квадрату абсциссы точки касания. 41. Найдите уравнение кривой, проходящей через точку А(0; е), если угловой коэффициент касательной к кривой в любой ее точке равен у. § 3. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 42. Скорость прямолинейного движения точки изменяется по закону v — 3t2 — 2t. Найти закон ее движения. О Известно, что скорость прямолинейного движения точки равна ds производной от пути s по времени t, т. е. v=—=3t2 — 2t, откуда ds = (3t2 — at
j(3/2 — 2t)dt; s—t3 — t2 + C. ф 43. Скорость прямолинейного движения точки изменяется по закону v = 3t2+4. Найти закон движения s, если за время t = 2 с точка прошла 20 м. ds О Так как v=—=3/2+4, то ds=(3t2+4)dt. Интегрируя, получим dt \ds=\(3t2+4)dt; s=t3+4t+C. Используя начальные условия, найдем 20 = 23 + 4 *2 +С, т. е. С=4. Итак, закон движения точки имеет вид s=f3 + 4/+4. ф
44. Найти закон движения свободно падающего тела при постоянном ускорении g, если в начальный момент движения тело находилось в покое. О Известно, что ускорение а прямолинейно движущегося тела есть вторая производная пути s по времени t или производная от скорости v по d2s dv dv времени t, т. е. а=—-^=—. Так как a=g, то —=g, откуда dv=gdt. dt dt dt Интегрируя, получим \dv=\gdt; V=gt + Cl. Используя начальные условия t=0, t? = 0, имеем 0=<g *0 + C1, т. е. ^=0. Таким образом, скорость движения тела изменяется по закону v=gt. IIU ^ ds ds Найдем теперь закон движения тела. Так как v=—, то ——gt, или dt dt ds=gtdt. Интегрируя, получим
45. Точка движется прямолинейно с ускорением a = 6t—12. В момент времени / = 0 (начало отсчета) начальная скорость v0 = 9м/с; расстояние от начала отсчета so = 10 м. Найти: 1) скорость и закон движения точки; 2) значения ускорения, скорости и пути в момент t = 2 с; 3) момент, когда скорость является наименьшей. dv О 1) Находим скорость: —=6/—12, или dv = (6t—12) dt. Интегрируя, dt получим \dv = \(6t-\2)dt; v=3t2-\2t+C1. Используя начальные условия t — 0, v0 = 9, имеем 9 = 3 О2 —12 0+Ci, т. е. Сi=9. Следовательно, i? = 3r2 — 12/Н-9. ds Находим закон движения точки: —=3/ — 12/Н-9, или ds=(3t — I2t+9)dt. dt Интегрируя, находим f ds=j (3t2 — \2t+9) dt; s=t3 — 6t2 + 9t+C2. Используя начальные условия /=0, 50 = Ю, имеем 10 = О3 — 6 О2+ 9 *0+С2, т. е. С2 = 10. Таким образом, s=t3 — 6t2 + 9t+10. 2) Найдем a, v и s при /=2: а=6 -2—12=0; v = 3 *22 —12 *2 + 9= —3 (м/с); 5=23—6 -22+ 9 -2 +10= 12 (м). 3) Исследуем функцию, определяющую изменение скорости, на максимум и минимум: v = 3t2 -\2t-\-9, v' = 6t— 12, 6t— 12=0, t = 2; v" = 6>0. Следовательно, скорость является наименьшей при t=2 с.- # 46. Скорость прямолинейного движения точки изменяется по закону: 1) v = t2 — 8f + 2; 2) v = 4t—3t2.Найдите закон движения точки. - 47. Скорость прямолинейно движущейся точки задана формулой v = 2t — 3. Найдите закон движения точки, если к моменту начала отсчета она прошла путь 6 м. 48. Скорость прямолинейного движения точки задана формулой v = 3t2+4t— 1. Найдите закон движения точки, если в начальный момент времени она находилась в начале координат. 49. Скорость прямолинейного движения точки задана формулой v= 2 cos t. Найдите закон движения, если в момент t=n/6 точка находилась на расстоянии s=4 м от начала отсчета. 50. Тело брошено вертикально вверх с начальной скоростью v0. Найдите закон движения этого тела (сопротивлением воздуха можно пренебречь). 51. Точка движется прямолинейно с ускорением a=12t2 + 6t. Найдите закон движения точки, если в момент t— 1с ее скорость г = 8 м/с, а путь s=6 м. 52. Точка движется прямолинейно с ускорением а=— 6^+18. В момент времени t = 0 (начало отсчета) начальная скорость v0 = 24 м/с, расстояние от начала отсчета s0 = 15 м. Найдите: 1) скорость и закон движения точки; 2) значения ускорения, скорости и пути в момент t=2 с; 3) момент, когда скорость является наибольшей. § 4. ИНТЕГРИРОВАНИЕ МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла J/ (jc) dx в интеграл \F(u)du, который легко вычисляется по какой-либо из основных формул интегрирования.
Для нахождения интеграла j/ (jc) dx заменяем переменную jc новой переменной и с помощью подстановки х=ср (и). Дифференцируя это равенство, получим dx=(p' (u)du. Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через и и du, имеем if М <fc=J/[<p («)] Ч>' (и) du=i F(u) du. После того как интеграл относительно новой переменной и будет найден, с помощью подстановки г/=\|/ (лг) он приводится к переменной jc. Найти следующие интегралы: 53. 1) J(3x+2)5 dx; 2) }(2x3+l)4x2dx; _ч Г xdx Г х2 dx 3>J<?7iF; 4)J^T- О 1) Введем подстановку 3x4-2 = и. Дифференцируя, имеем 3dx=du, откуда dx=(l/3)du. Подставив в данный интеграл вместо 3x4-2 и dx их выражения, получим |(3Л+2)^=1|„^И=1-1-+С=1«6+С. Заменив и его выражением через х, находим (3x+2)5fifcc=-^M6 + C=-^(3jc+2)6 + C. J 18 18 Проверка: d -^-(Зх+2)6 + С =^-(3x-b2)5-3dx=(3x+2)5dx. 118 I 18 2) Положим 2х3 +1 =и, откуда 6x2dx=du, х2 dx=(\/6)du. Таким j*(2x34- l)4x2dx=-j*M4dM=-- — + С=—м5 + С=—(2х34-1)5 +С. 3) Полагая х2 + 1=м, имеем 2xdx=du, xdx=(\/2)du. Значит -Ч-^+с--5.+с- ■+С. 4(х24-1)2 Положим 5х34-1 = м, откуда 15x2dx=dM, x2dx=(1/15) dM. Поэтому х2 dx 1 Г du 1 1 - t5FTT=T5j7=i5ln“+c=T5ln|5jc +1|+с • . 1) ftgkxdx; 2) f—; 3) J J sm м J cos м I I sin dx О 1) Имеем tgfcxdx=---------------- —. Положим cos kx = u, откуда J J cos kx iin /ex dx=dw, sin kx dx = — (1/A:) dw. Следовательно, f 1 fdw 1 1 tg kx dx = —= — — In | г/1 +C= — - In I cos kx | +C. J k] и k k
2) Так как sin м=2 sin (м/2) cos (м/2), то du m/2) cos (m/2) Разделив и умножив знаменатель на cos (м/2), получим du Г *_.i Г_ Jsmu 2jtg(u/: w/2)cos2 (m/2)
1,, __________ cos2 (m/2) 2 Z’ e* cos2 (m/2) образом,
3) Имеем | — |—Положим ^4-m=z, тогда du=dz. По- sin ( этому О 1) Положим 5х2 = и, откуда 10xdx—du, xdx=(l/10)dw. Значит,
Г if 13“
2) Положим — Зх24- 1 = w, откуда —6xdx = du, x dx — — (1 /6) du. Таким образом, ^e~3xl+i xdx= - X-^eu du= ~^eu+C= - Х-е-3х2+' + C. •
J v* Jc cos2 2x2* О 1) Положим y/x=u, откуда dx/(sfx)=2du. Следовательно, dx=2 J sin udu= —2 cos u+C= —2 cos yfx+C. 2) Положим 2x2 = w, откуда 4xdx=dw, xdx=(\/4)du. Таким образом, Г 3xdx 3 Г du 3 3
Г 3х dx Г cos xdx ‘ ' J \j25—9* ; ^ JiW7
du 1. и 1. 3х ^
§ 5. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ Интегрируя обе части равенства d(uv) = udv + vdu, получим J d(uv) = $udv + \vdu\ uv=$udv+$vdu, откуда \udv = uv—\vdu. (11.14) С помощью этой формулы вычисление интеграла J udv сводится к вычислению интеграла \vdu, если последний окажется проще исходного. 74. Найти следующие интегралы: 1) JxsinxAr; 2) J—3) j%4/x2 + a2 dx. О 1) Положим и=х, dv = sin х dx; тогда du= dx, J dt; = J sin x dx:, т. e. v = — cos x. Используя формулу (11.14), получим J л: sin xdx— —jccosjc+J cos xdx= —xcosx+sinx+C. , dx J dx L [dx f -2J 2) Положим u= \nx, dv=—; тогда du =—, \dv= — = x dx= = — v= — По формуле (11.14) получим X X fin л:, lnx Cl dx \nx Г 0, \nx 1 \—dx= -------------- +----------- =---------- + \x~2dx = --------------------- + C. J xz X J X X X J XX 3) Положим u=y/x2 + a2, dv = dx; тогда du—- X-X -, v=x. По форму- y/x2 + a2 ле (11.14) получим f Jx2 + a2 dx=xy/x2 + a2 — f В числителе подынтегральной функции последнего интеграла прибавим и вычтем а2 и представим этот интеграл в виде суммы двух интегралов: Г Гг- 2"j Гг ----- 2 fx2 + a2-a2 г— --- т Г х2 + а2 Jx^ + a* dx — x Jxz + az — — - — dx — xjхл + а.1 — — -dx+ Jv V J V ijs+a* dx 2 Г Й + <Z I —r— J Jp Последний интеграл находим по формуле (11.11): f у/х2 + а2 dx—xyfx2 + a2 —\у/х2 + а2 dx+a2 In |x+y/x2 + a2 | +C. Перенеся j yjx2 + a2 dx из правой части в левую, получим 2\Jx2 + a2 dx=xy/x2 + a2 +tf2ln \х+^/х2 + а2 | + С,
х2 + а2 dx=^xy/x2 + a2 + ^-ln| х+у/х2 + а2 \ +С. # Найдите следующие интегралы:.75. 1) Jxcosxdx; 2) j(l — х) sinjtdk. 76. 1) 2) yn2xdx. 77. 1) \xexdx; 2) |4^-. J J sin x 78. 1) | arcsin xdx; 2) farctgxdx. 79. 1))excosxdx; 2) jexsinxdx. 80. Проверьте равенства интегрированием по частям: 1) J y/x2 —a2 dx—\-x у/ х2 — a2 — ^-ln | х+ y/x2 — а2 | +С; 2) ^у/а2—х2 rfjt=y arcsin^ + ^у/а2—х2 +С. § 6. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ При вычислении интегралов вида j sin2" х dx или j cos2".г dx от четной степени синуса или косинуса используются формулы понижения степени ., 1— cos 2х 9 14-cos 2х sinx =--------;, cos х=. 2 2 При вычислении интегралов вида jsin2”+1 xdx или Jcos2n+1 xdx от нечетной степени синуса или косинуса нужно отделить от нечетной степени один множитель и ввести новую переменную, полагая cos x=t в первом интеграле и sin x=t—во втором. При вычислении интегралов вида j sin сих cos рлг dx, J sin ax sin px dx и j cos ax cos fixdx применяются формулы sin ax sin px=^ [cos (a—P) x—cos (a 4- P) x], cos ax cos px=- [cos (a—P) x+cos (a4- p) x], sin ax cos px=^ [sin (a—p) x+sin (a4- P) x]. Найти следующие интегралы: 81. 1) Jcos2 xdx; 2) Jcos*xdx. О 1) Заменяя cos2x на (14-cos 2x)/2, получим
2) Jcos4xdx=J(cos2x)2dx=^ dx=-Jdx+- Jcos2xd!x4-
Jcos4 x<fa'=-x+ - sin 2ж+ - J”(l +cos4л:)Л=-х+ -sm2x+ — sin4x+C= 1 1 =-x+ -sin2x4- — sin4x+C. # 82. 1) Jtg2 xdx; 2) Jt%Axdx. О 1) Воспользовавшись соотношением tg2x=—; 1, получим cosz x {tg2x<fe=J(^k-1)'fa=I^"Idx=tg"“x+c Вычислим первый интеграл. Полагая tg х=м, найдем dx/(cos2 х) = du и, следовательно, Использовав результат предыдущего примера, окончательно получим J*tg4x</x=^—^-tgx+x+C. ф 83. 1) J sin3 xdx; 2) Jtg3xdx. О 1) | sin3 x dx=J sin2 x sin x dx=J (1 — cos2 x) sin x dx. Положим cos x=u; тогда—sin xdx=du и, следовательно, (* Г I/3 COS3 X sin3 xdx= — (1 —u2)du=—u+ — +C= — cosxH-- h C. 2) Jtg3^=Jtg^tgx^=J Г w ч fsinxdx 1 _ = tgxd(tgx) — ------------- =-tg2x4-ln|cosx| + C. ф J J cos x 2 84. 1) J sin5xsin3xrfx; 2) J cos 4x cos x dx; 3) J sin 7x cos 3x dx. f if 1/1 1 \ О 1) sin 5x sin 3xdx=- (cos 2x—cos 8x) t/x=— I — sin 2x— - sin 8x I 4- C= 1 1 =- sin 2x------ sin 8x4- C. 3 16 f if 1/1 1 \ 2) cos4xcosxdx=- (cos3x4-cos5x)dx=-l -sin 3x4- -sin5x I 4-C= =\ sin ЗхН- jt sin 5x4- C. 6 10 f If 1/1 1 \ 3) sin 7xcos 3xdx=- (sin4x+sin lOx) dx=-I — -cos4x— ^cos Ю* I 4- 4- C= — ^cos4x—— cos 10x4-C. ф 8 20 Найдите следующие интегралы: 85. 1) j* sin2 xdx; 2) J sin4 xdx. 86. 1) Jetg2xdx; 2) J ctg4 xdx. 87. 1) Jcos3 xdx; 2) J sin5 xdx; 3) Jcos5 xdx:; 4) J ctg3 xdx. 88. 1) J sin 3x sin x dx; 2) J cos 5x cos 3x dx; 3) J sin 4x cos 3x dx. § 7. СМЕШАННЫЕ ЗАДАЧИ 89. Найдите функцию, производная которой / = sin2x—хе3х24-1. 90. Найдите, если при х=п\2 значение первообразной J cosx4-e функции равно 2. 91. Составьте уравнение кривой, проходящей через точку А (я/3; 2), если угловой коэффициент касательной к кривой в каждой ее точке равен cos (х/2). 92. Скорость прямолинейного движения точки задана формулой t; = sin2f. Найдите закон движения точки, если в момент t = n/6 она находилась на расстоянии 0,75 м от начала отсчета. 93. Точка движется прямолинейно с ускорением а=(—6f+24) м/с2. В момент времени /=1 с ее скорость v= 15 м/с, а пройденный путь = 20 м. Найдите: 1) закон изменения скорости точки; 2) закон движения точки; 3) ускорение, скорость и путь в момент /=3 с; 4) момент времени, когда скорость точки будет наибольшей. Найдите следующие интег
J 1—cosx J 9+sin х 8. J sin2 x cos2 xdx. 99. J sin 5x cos xdx. ЗАЧЕТНАЯ РАБОТА
I вариант Найдите интегралы: J ху/х 3) • J Sin X COS X 4) Составьте уравнение кривой, проходящей через точку (—2; 8), если угловой коэффициент касательной в любой точке касания равен 2х—4. 5)Скорость прямолинейного движения точки v = 3t2 + 6t—4. Найдите закон движения точки, если за время г=2с она прошла путь 8 м. II вариант Найдите интегралы: „ Г-Д-У^-% J ху/х 2) Jbb+?b 3) J(4sin2 х cos х—cos x) dx. 4) Найдите уравнение кривой, проходящей через точку А (п/3; 1/2), если угловой коэффициент касательной к кривой в каждой ее точке равен sinx. 5) Точка движется прямолинейно с ускорением a = 6/+ 6. Найдите закон движения точки, если 5=0 в момент времени / = 0, а в момент времени t=3 с скорость г=40 м/с.
Глава 12 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО НЕПОСРЕДСТВЕННОЕ ВЫЧИСЛЕНИЕ Пусть функция /(х) определена на отрезке а^х^Ь. Разобьем этот отрезок на п частей точками а<х0<х1<х2<...<х„ = Ь, выберем на каждом элементарном отрезке хл_!<х<хл произвольную точку £к и обозначим через Ахк длину каждого такого отрезка. Интегральной суммой для функции f(x) на отрезке а^х^Ь называется сумма вида £ /(ддх^дуд*, +/(УДх2 +...+/(уЛх„. fc= 1
f(x)dx= lim £ /(У Ахк max Ajck—*0 к = 1 Для любой функции /(х), непрерывной на отрезке а^х^Ь, всегда ь существует определенный интеграл J f(x)dx. а Для вычисления определенного интеграла от функции /(х) в том случае, когда можно найти соответствующий неопределенный интеграл ^(х), служит формула Ньютона — Лейбница:
т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования. Вычислить следующие определенные интегралы: 13 2 1) J xdx; 2) J х2 dx; 3) J (х2 + 2х+ 1) dx. о 2 -i О По формуле Ньютона—Лейбница получаем:
1 1 1 =;(12-о2И; о 3 1,., 19 =;(33-2W; 3) |(^+2x+1)^=^3+x2+xJ2i=^-23 + 242J-^(-1)3 -1 +(-1)Ч(-1)]=9. • 1 е 1. 1) | exdx; 2) I -1 /*-
N/2 2.
я/6 я/3 js?r -(f - ')-3 я/4 V3/2 1
-1 V3/2 [ dx. I^2. Уз. *
J я ’ 1 1 V ■
f dx 2) Jtt?-"18* л 71 Л Я = arctg 1—arctg 0=—0=-. ф о 4 4
Вычислите следующие определенные интегралы: 2 3 5. 1) \x2dx 2) fx3dx; 3) fx4dx. Oil з о 6. 1) j (4x> — 3x2 + 2x+l )dx; 2) J (x3-+2x)dx:. -2-1 1 1/2 4 7. 1) | J; 2) jj; 3) 1/2 1/3 0 8 27 8. 1) [\fPdx-, 2)
9. 1) \e2xdx; 2) \e3xdx. о 10- ■> jr: 2> \h -3) 4> fx+r я/3 я/4 я/2 и. l) J sinxrfx; 2) J cos xdx; 3) J (cos x — sin x) dx. О —я/4 —я/2 я/4 я/4 я 12. 1) f cos2 xdx; 2) J sin4.xdx; 3) Jcos(x/2 )dx.
я/4
*
J cos^x
16. § 2. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ При вычислении определенного интеграла методом замены переменной ъ (способом подстановки) определенный интеграл {/(х) dx преобразуется с а помощью подстановки и=\|/(х) или х=ср (и) в определенный интеграл относительно новой переменной и. При этом старые пределы интегрирования а и b заменяются соответственно новыми пределами интегрирования а и Р, которые находятся из исходной подстановки. Из первой подстановки новые пределы интегрирования вычисляются непосредственно: а=\|/(я), Р = \(/(б). Из второй подстановки новые пределы интегрирования находятся путем решения уравнений а=ф(а) и & = ф(р) относительно аир. Таким образом, имеем 17. Вычислить определенные интегралы: 2 1 V3/3 1) V2/3 О 1) Введем новую переменную интегрирования с помощью подстановки 2х— 1=и. Дифференцируя, имеем 2dx=du, откуда dx=(\/2)du. Находим новые пределы интегрирования. Подставляя в соотношение 2х—\=и значения х=2 и х=3, соответственно получим мн = 2*2—1=3, ив = 2-3 —1 = 5. Следовательно, 3 5
|(2х-1)3Лс=^ 2) Положим 5х— 1=м; тогда 5dx=du, dx = (l/5)du. Вычисляем новые пределы интегриров
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.25.152 (0.016 с.) |

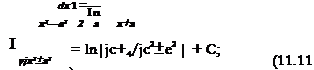
 dx x
dx x y/a*=Z-
y/a*=Z- dx 1 x
dx 1 x О 1) По формуле (11.4) при я = 2 получим
О 1) По формуле (11.4) при я = 2 получим Так как (\/5)d(5x—3) = dx, то cos (5л:—3) dx
Так как (\/5)d(5x—3) = dx, то cos (5л:—3) dx О 1) По формуле (11.8) находим
О 1) По формуле (11.8) находим x2 dx if d(x3) 1
x2 dx if d(x3) 1 =-tgx3 + C.
=-tgx3 + C. dz 1
dz 1 ;^и)=_Ь‘8(х2+1)+с- •
;^и)=_Ь‘8(х2+1)+с- •






 Мы нашли совокупность (семейство) кривых, для которых угловой коэффициент касательной в любой точке равен 2х. Эти кривые отличаются друг от друга на постоянное слагаемое С. При С=0 получим параболу у — х2 с вершиной в начале координат, при С— 1—параболу у=х2 +1 с вершиной в точке (0; 1), при С= —2—параболу у—х2 —2 с вершиной в точке (0; —2) и т. д. (рис. 66). ф
Мы нашли совокупность (семейство) кривых, для которых угловой коэффициент касательной в любой точке равен 2х. Эти кривые отличаются друг от друга на постоянное слагаемое С. При С=0 получим параболу у — х2 с вершиной в начале координат, при С— 1—параболу у=х2 +1 с вершиной в точке (0; 1), при С= —2—параболу у—х2 —2 с вершиной в точке (0; —2) и т. д. (рис. 66). ф №
№ Используя начальные условия /=0, 5=0, имеем 0=g-02/2 + C2, С2 = 0. Итак, закон движения падающего тела имеет вид s=gt2/2. #
Используя начальные условия /=0, 5=0, имеем 0=g-02/2 + C2, С2 = 0. Итак, закон движения падающего тела имеет вид s=gt2/2. #
 z| 4-С=In | tg (m/2) | +C.
z| 4-С=In | tg (m/2) | +C.
 5x2 xdx=— I 3й du—— -—- +С= J 10 J 10 In 3
5x2 xdx=— I 3й du—— -—- +С= J 10 J 10 In 3 56. 1) [^ф-dx; 2) f-
56. 1) [^ф-dx; 2) f- —2~^~2=1 —=-tgw-bC=-tg2x" J cos 2д: 4 J cos м 4 4
—2~^~2=1 —=-tgw-bC=-tg2x" J cos 2д: 4 J cos м 4 4 О 1) Полагая 3х — щ находим 3xln3dx=dw, V/25^9X =х/25^«2^. Следовательно,
О 1) Полагая 3х — щ находим 3xln3dx=dw, V/25^9X =х/25^«2^. Следовательно,


 или окончательно
или окончательно f. j [*1 H-cos 2x 1 f If cos xdx= 2 2 °
f. j [*1 H-cos 2x 1 f If cos xdx= 2 2 ° ■U-
■U- тегралы: 95. e^cosx^/e
тегралы: 95. e^cosx^/e Г sinxd!x Г cosxdx >• I--------------. 97. I =—.
Г sinxd!x Г cosxdx >• I--------------. 97. I =—.
 Определенным интегралом от функции f(x) на отрезке а^х^Ь называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю: ь
Определенным интегралом от функции f(x) на отрезке а^х^Ь называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю: ь
 f(x)dx=F(x)
f(x)dx=F(x) 1
1


 1
1 1) Jcos xdx:; 2) j*
1) Jcos xdx:; 2) j* /6 ф
/6 ф 1 ■> J Ж? 2) Ji
1 ■> J Ж? 2) Ji , = arcsin x = arcsin arcsin (— 1)=-
, = arcsin x = arcsin arcsin (— 1)=-
 4> Ы*-
4> Ы*- о
о ~ ^ ч Г 4dx
~ ^ ч Г 4dx 1) —;
1) —;

 j*(2x-lfdx\ 2) J—==; 3) j*(2x3+l)[25]x2dx; 4) J _
j*(2x-lfdx\ 2) J—==; 3) j*(2x3+l)[25]x2dx; 4) J _


