
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тело массой 10 кг движется прямолинейно По законуСодержание книги
Поиск на нашем сайте
= 3t2 + Г-1-4. Найти кинетическую энергию тела (mv2/2) через 4 с после начала движения. О Найдем скорость движения тела в момент времени t: ds v=—=6t+\. Вычислим скорость тела в момент /=4; v(4)=6 *4+1 = 25(м/с). dt Определим кинетическую энергию тела в момент / = 4: mv2/2= 10 * 252/2 = = 3125 (Дж).# 41. Сила тока / изменяется в зависимости от времени t по закону 7=0,4/2 (7—в амперах, t—в секундах). Найти скорость изменения силы тока в конце 8-й секунды.
42. Найдите скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением: 1) s = t3 + 5t2 + 4, /=2; 2) s = y/t, t= 1; 3) s = t2 + Ш + 30, t = 3. 43. Найдите ускорение точки в указанные моменты времени, если скорость точки, движущейся прямолинейно, задана уравнением: v = t2 + t— 1, /=3; 2) i; = /2 + 5/+l, t=3. 44. Точка движется прямолинейно по закону s=t2 — 8/+4. В какой момент времени скорость точки окажется равной нулю? 45. Температура тела Т изменяется в зависимости от времени t по закону Г=0,5/2 —2/. С какой скоростью нагревается это тело в момент времени / = 5? 46. Тело массой 100 кг движется прямолинейно по закону s = 5t2 — 2. Найдите кинетическую энергию тела через 2 с после начала движения. 47. Изменение силы тока 7 в зависимости от времени t дано уравнением I=2t2 — 5t (7—в амперах, t—в секундах). Найдите скорость изменения силы тока в конце 10-й секунды.
х_1’ -• ' 2+х 54. 1) у=\% 10.x;2) j=lg(2x+l). 55. 1) у=1п^/2х-1; 2) >»=1п у/х2-а2; 3) j=lg4/x2+4; 4),-In /В. \ 1 +х 56. 1) jk = 1п3Злг; 2) }> = ln2(2x+1); 3) у = ln2(x2—1). § 7. ПРОИЗВОДНЫЕ ПОКАЗАТЕЛЬНЫХ ФУНКЦИЙ Формулы дифференцирования
Найти производные следующих функций: 57. у = 2'5х + 3ех. О По формулам (7.1), (7.15а), (7.16а) и (7.4) получим / = 2 • 5х In 5 + Зех = 2 In 5 • 5х+3ех. ф 58. /(x)=^il; вычислить /'(—1). О I способ. Применив формулы (7.5), (7.1), (7.16а) и (7.9), получим (ех+\),(ех-\)-(ех-\)'(ех+\)_ех(ех-\)-ех(ех+\) 2ех J (Х’~ (е*— I)2 " (е*—I)2 “ (е*-1)2'’ /.(_!)— ICl—-*_ ' (<Г‘-1)2 (1-е)2 II способ. Прологарифмировав функцию, находим производную логарифма: In f(x) = In (е* 4-1) — In (е* — 1); _1, _____________ е* = -2е* f(x) ^4-1 е*—1 (ех+1)(ех— 1) Следовательно, 59. 1) у = 32*2; 2) у=<Г2*. О 1) По формуле (7.15) получим у = з2*2 In 3 • (2х2у = З2*2 In 3 * Ах—Ах * 32х In 3. 1) По формуле (7.16) находим у =е-2х(-2хУ=е-2х-(-2)=-2е-2х. • Найдите производные следующих функций: 60. 1) /(х)=1п;с-е*; 2) f(x)=x2ex; 3) f(x)=ex-xex; 4) у=3V; 2) у=ех/2х', 6) /(х)=51пл:+ех; вычислите /'(1). ,ч 5-*1. ЛЧ 1~«‘ 6L!) 2) 62. 1) у=5х3; 2) у=2"1х\ 3) у=3,пх. 63. 1) у = е~**; 2) у=е^х; 3) у=е1пх. 64. 1) у=3(ех/3—е~х/3); 2) § 8. СМЕШАННЫЕ ЗАДАЧИ Найдите производные следующих функций: 14 *+1 04 /•/ \ Х3+\, V Х3 + 1 65. 1) г; 2) /(х)=-----------; вычислите /(1); 3) j=-T— лс 1 X X I 1 4) Лм)=ц2+зц+2; вычислите /'(0). 66. 1) s=y/t+\ft; 2) j=-^=—^=; 3)/(x)=N^1; вычислите/'(4); Vх Vх V1 4) /(x)=4+v^; вычислите /'(1). ДУ X 67. 1) f(t)=(r + f)3-, вычислите /'(1); 2) у =; 2) J=(3^1)3; 4) f(x)=(x2-l)2 vV + 1; вычислите /'(>/3). 68. 1) /(м) = >У2 + ^/2м; вычислите /'(2); 2) /(х) = у/5х2+2л: 4-1; вычислите /'(—1); 3) у= J -аХ; 4) f(z) = ^; вычислите /'(^/5). \/ 1 — ^ JC3 //х 1 69. 1) /(*)=——=; вычислите/'(1); 2) Дх)= 1^-=—; вычислите V8+x3 \V*+1 /'(4); 3) /(*)=---------- 7 =='> вычислите /'(>/3). Х-\- yj X 70. 1) >'=ln^Y^; 2) >'=1п(х-х/Г+х5); 3) j=ln(x-N/x2-1); 3) in^+V^zl; 5) j; = ln 6) j;=lnv/x-lnx2. х-ф^-Х yl-ax 71. 1) y=y/e3x; 2) j>=;te2*. ЗАЧЕТНАЯ РАБОТА
0 /М=Г^+Ь+ + 6х2у/х; найдите /'(1). 2) /(х)=(х2—2) у/х +1; найдите /Ш 9 z 3) /(2)=—==; найдите Vz2 +1 /'(2^2). 4) /(х)=е2Мпх2; найдите /'(1). 5) Точка движется прямолинейно по закону s=2t3 —2t2—4 (j—в метрах, t—в секундах). Найдите ускорение точки в конце 2-й секунды. •) /М=-з+777=-^=+Зх- * 2\[х фс —2х2*/х; найдите /'(1). 2) /(м)=(м2 + 3) у/и2—1; найдите /Ш 3) /(*)=- i-V^+т’ /Ш 4) /(лг)=%/?1пл:2; найдите /'(1). 5) Точка движется прямолинейно по закону s=2t3 — 3t2+4 (s—в метрах, t—в секундах). Найдите ускорение точки в конце 3-й секунды.
Глава 8 ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ § 1. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ Функция у = /(х) называется возрастающей в промежутке а<х<Ь, если для любых xt и х2, принадлежащих этому промежутку и таких, что х1<х2, имеет место неравенство f(xi)<f(x2). Функция у = /(х) называется убывающей в промежутке и<х<Ь, если для любых хх и х2, принадлежащих этому промежутку и таких, что х1 <х2, имеет место неравенство f(xl)>f(x2). Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает,—промежутками монотонности. Возрастание и убывание функции у = /(х) характеризуется знаком ее производной: если в некотором промежутке /' (х)> 0, то функция возрастает в этом промежутке; если же /' (х) <0, то функция убывает в этом промежутке. Найти промежутки монотонности следующих функций: 1. 1) f{x)=x2 — 8д:+12; 2) f{x) = х3 — 6л:2 + 4. О 1) Находим производную: /'(х)=2х—8; имеем (2х—8 = 0)о(х=4). Последующие рассуждения представим в таблице:
Таким образом, данная функция в промежутке — oo<jc<4 убывает, а в промежутке 4<х<оо возрастает (рис. 23). 2)
/(*) Итак, в промежутках — оосхсО и 4<х<оо функция возрастает, а в промежутке 0 с* <4— убывает (рис. 24). ф 2. 1) j=—; 2) у=1пх; 3) y=Jx~x2. О 1) Область определения данной функции—вся числовая прямая, кроме точки х=0. Находим у'= — \/(2х2). Очевидно, что у’<0 при всех х из области определения функции, т. е. функция у=\/(2х) убывает в промежутках — оосхсО и 0<х<оо (рис. 25). 2) Область определения функции—промежуток Осхсоо. Очевидно, что производная у'= 1/х в этом промежутке положительна. Следовательно, функция у = \пх в промежутке 0 < jc < оо возрастает. 3) Для нахождения области определения функции решим неравенство х—х2^0, откуда получаем O^x^l. Таким образом, данная функция определена в промежутке 0<х<1. 1 — 2х Найдем производную у'=—----- ------. Так как знаменатель дроби 2 yj х х
Следовательно, в промежутке 0<х<1/2 функция возрастает, а в промежутке \/2<х<\—убывает. # Найдите промежутки монотонности следующих функций: 3. 1) /(х)=х[8] — 6x4-5; 2) /(х) = 2х2 —4x4-5; 3) Дх) = —х24-4x4-1. 4. 1) /(х) = х[9] — Зх24- 1; 2) /(*)= — ^х34-^х24-2. 5. I) f(x)=x*-4x+3; 2) f(x)=x*-32x+40; 3) Дх)= —ijc [10] —jc+1. 6. 1) /(х) = 2х3—9х4-12х—15; 2) /(х) = —2х34-15х2 — 36x4-20. 7. 1) /М—1; 2) 8. 1) у=1пх2; 2) =In 9* 1) У=^х2 — 1пх1 2) _у=1пл:—^л:3. 10. 1) у=е~х; 2) у=е*2; 3) j>=e1/x. 11. 1) y=\Jx—2л:2; 2) у = ^/х? — Зх. § 2. ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЭКСТРЕМУМ С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ Точка х0 из области определения функции f(x) называется точкой минимума этой функции, если существует такая 8-окрестность (х0—8, х04-5) точки х0, что для всех хФх0 из этой окрестности выполняется неравенство f(x)^f(x0). Точка х0 из области определения функции /(х) называется точкой максимума этой функции, если существует такая 8-окрестность (х0—8, х04-8) точки х0, что для всех х#х0 из этой окрестности выполняется неравенство /(*)</■(*<>)• Точки минимума и максимума функции называются экстремальными точками (или точками экстремума) данной функции, а значения функции в этих точках—минимумом и максимумом (или экстремумами) функции. Точками экстремума могут служить только критические точки, т. е. точки, принадлежащие области определения функции, в которых производная /' (х) обращается в нуль или терпит разрыв. Если при переходе через критическую точку х0 производная /' (х) меняет знак, то функция /(х) имеет в точке х0 экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум—когда с плюса на минус. Если же при переходе через критическую точку х0 производная /' (х) не меняет знака, то функция /(х) в точке х0 не имеет экстремума. Пр авило нахождения экстремумов функции y=f(x) с помощью первой производной этом критическая точка х0 есть точка минимума, если она отделяет промежуток, в котором /'(л;)<0, от промежутка, в котором /'(*)> 0, и точка максимума—в противном случае. Если же в соседних промежутках, разделенных критической точкой х0, знак производной не меняется, то в точке х0 функция экстремума не имеет. IV. Вычислить значения функции в точках экстремума. Исследовать на экстремум следующие функции: 12. \) f (х) = х2—4х; 2) /(*)= — л;2 + 5л:+6.
График функции f (х)=х2—4х есть парабола, изображенная на рис. 26. Точка минимума (2; —4) является вершиной параболы.
13. 1)/(х)=^х4; 2) f (х)=х3—Зх2.
График функции f(x)=x3 — 3x2 изображен на риЬ. 29. ф 14. f (х) = \/хт (х- 5).
о Находим / (х)=—=(х-5) +\fx*= —— В 35Д ъ\£ 3 V* ном случае критическими являются точки х=0 (в ней производная терпит разрыв) и х—2 (в ней производная обращается в нуль). Составим таблицу:
График функции f(x) = \fx2(x—5) изображен на рис. 30. ф Исследуйте на экстремум следующие функции: 15. 1) / (х)=х2—х; 2) f(x)=x2 + 3x. 16. 1) f (x)= — х2+2х; 2) f(x)=—x2—x. 17. I) f(x)=x2-8x+\2; 2) f(x)=x2-4x+3; 3)f(x)=x2-\0x+9. 18. l)f(x)=-x2 + 2x+3-, 2) f(x)=-x2-x+ 6. 3) /(*) = = — 2x2+x+l. 19. 1) f(x) = 2x4 —x; 2) f (x)= — ^x4+8x. 20. \) f(x)=-x3-4x; 2) f{x) = X-x3-x2. 21. I) f(x) = 2x3-9x2 + l2x-8; 2) f(x) = 2x3-3x2-I2x+S; f (x) = 2x3 + 9x2 + \2x — 2. 22. 1) / (x) = 5—2\/x2; 2) f(x) = 33J^-x. 23. I) f(x)=63^T(x+l); 2) f(x)=X/^(10-x). 24. I) f(x)=ex+e~x; 2) f(x)=x2e~x. 25. 1)/(jt)=jt—21nx; 2) /(x)=xlnx. § 3. ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЭКСТРЕМУМ С ПОМОЩЬЮ ВТОРОЙ ПРОИЗВОДНОЙ Если/ есть производная от функцииy=f (х), то производная от у' по х (если она существует) называется второй производной (или производной второго порядка). Для второй производной употребляются следующие обозначения: „ „ d2y d2f(x) у, ух, —2 или / (*), Пра вило нахождения экстремумов функции y=f(x) с помощью второй производной I. Найти производную fix). И. Найти критические точки данной функции, в которых /' (х)=0. III. Найти вторую производную /"(*)• IV. Исследовать знак второй производной в каждой из критических точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то—минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной. V. Вычислить значения функции в точках экстремума. 26. Исследовать на экстремум с помощью второй производной функции: 1) /(х) = х2 — 2х—3; 2) /(х) = х3 —9х2 + 24х—12. О 1) Находим производную: /'(*) = 2х—2. Решая уравнение /'(*)=О, получим критическую точку х=1. Найдем теперь вторую производную: /" (х) = 2. Так как вторая производная в критической точке положительна, то при х= 1 функция имеет минимум: /min =/(1) = —4. 2) Находим /'(х) = 3х2 — 18x4-24; (Зх2— 18х4-24=0)<*>(х2 — 6х4-8 = 0)о Г х=2, о\ ’ Найдем теперь /"(х) = 6х—18. Определим знак второй производ- L*=4. ной в критических точках. Так как /" (2) = 6-2 —18<0, то при х=2 функция имеет максимум; так как /"(4)=6-4—18>0, то при х=4 функция имеет минимум. Вычислим значения функции в точках экстремума: /тах = / (2) = 23 — йй-9-224-24-2-12 = 8, /min=/(4)=43-9*424-24-4-12=4. • Исследуйте на экстремум с помощью второй производной следующие функции: 27. 1) /(х) = 2х2 —3; 2) /(х) = х2-2х; 3) /(х) = 2х2-5х+2; /(х) = — х24-4х; 5) /(х) = — х24-х4-6. 28. 1) /(х)=^х3 —2х24- 3x4-4; 2) /(х)=^х3 —Зх24-5х4-5; /(x) = x3—^x24-6x—2; 4) /(x) = x44-3x2 —4. 29. 1)f(x)=^-; 2) /W=^y. Для нахождения наименьшего и наибольшего значений функции, непрерывной в некотором промежутке, необходимо: 1) найти критические точки, принадлежащие заданному промежутку, и вычислить значения функции в этих точках; 2) найти значения функции на концах промежутка; 3) 30. Найти наименьшее и наибольшее значения функции f(x) = x2 —4х+3 в промежутке О^х^З. О Имеем /' (х)=2х—4; 2х—4=0, т. е. х=2—критическая точка. Находим / (2) = — 1; далее, вычисляем значения функции на концах промежутка: / (0) = 3, /(3) = 0. Итак, наименьшее значение функции равно —1 и достигается ею во внутренней точке промежутка, а наибольшее значение равно 3 и достигается на левом конце промежутка (рис. 31). ф Найдите наименьшее и наибольшее значения функций в заданных промежутках. 31. 1) f(x) = x2 — бх+13, 0<д:<6; 2) f (х) = 8—0,5х2, 32. 1) f(x) = ^x2— ^х3, 1<х^3; 2) /(*) = 6х2 — х3, 33. l)/(x) = x3 —3*2-9х + 35, -4<х<4; 2) /(*)= -*3 + 9*2- -24х+10, 0<х^3. § 5. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШИХ И НАИБОЛЬШИХ ЗНАЧЕНИЙ ВЕЛИЧИН 34. Из всех прямоугольников данного периметра найти тот, у которого площадь наибольшая. О Пусть периметр прямоугольника равен р. Обозначим длину одной из р—2х сторон прямоугольника через х, тогда длина другой стороны равна —-—= р =^ — х. Обозначив площадь прямоугольника через у, имеем
Исследуем функцию на максимум и минимум с помощью второй производной: Вторая производная отрицательна, следовательно, функция имеет максимум при х=р/4. Таким образом, из всех прямоугольников данного периметра наибольшую площадь имеет квадрат. # 35.
щенность Е обратно пропорциональна квадрату расстояния от источника света и прямо пропорциональна косинусу угла падения (угла, образованного нормалью к поверхности с направлением светового потока), т. е.
где к зависит от силы источника света, помещенного в точке А (рис. 32). Из треугольника ОАВ имеем cos ос=Л/r и r=y/h2 + a2. Приняв h за независимую переменную, получим
Исследуем функцию на экстремум с помощью первой производной:
(h2+a2f
Так как £'>0 в промежутке 0<h<a/y/2 и Е'<0 в промежутке а/у/2 < <й<оо, то при h=ajyj2 функция имеет максимум, т. е. при значении h=aly/l «0,7а освещенность в точке В является наибольшей. # 36. Закон прямолинейного движения тела задан уравнением s= — t3 + 9t2 — 24/—8. Найти максимальную скорость движения тела (^—в метрах, /—в секундах). О Скорость движения тела есть первая производная от пути по времени: i?=s" = — 3/24-18/—24. Исследуем эту функцию на максимум и минимум с помощью второй производной: t?" = — 6/4-18; -6/4-18=0; / = 3; v" = —6. Вторая производная отрицательна, следовательно, скорость является наибольшей при^=3. Найдем значение скорости в момент /=3: v (3)= — 3 * З2 4-18 • 3—24 = 3 (м/с). • 37. Сумма двух положительных чисел равна а. Каковы эти числа, если сумма их кубов является наименьшей? 38. Произведение двух положительных чисел равно а. Чему равны эти числа, если их сумма Является наименьшей? 39. Каким должен быть прямоугольник наибольшей площади, который можно согнуть из куска проволоки длиной 50 см? 40. Из всех прямоугольников Данного периметра 2р найдите тот, у которого диагональ наименьшая. 41. Из всех прямоугольников, вписанных в круг радиуса R, найдите тот, который имеет наибольшую площадь. 42. В полукруг радиуса R впишите прямоугольник наибольшей площади. 43. В полукруг радиуса R впишите прямоугольник наибольшего периметра. 44. Из всех треугольников, у которых сумма основания и высоты равна а, найдите тот, у которого площадь наибольшая. 45. В круг радиуса а вписан равнобедренный треугольник. При каком соотношении сторон треугольник будет иметь наибольшую площадь? 46. В треугольник, основание которого а и высота h, вписан прямоугольник наибольшей площади (основание прямоугольника лежит на основании треугольника). Найдите длины сторон прямоугольника. 47. В прямоугольный треугольник, катеты которого равны а и b, вписан прямоугольник наибольшей площади так, что одна из его сторон лежит на гипотенузе. Найдите длины сторон прямоугольника. 48. В равносторонний треугольник с периметром Ът вписан прямоугольник наибольшей площади. Найдите длины сторон прямоугольника. 49. Закон прямолинейного движения тела задан уравнением s=— /3 + 3/2+9/+3. Найдите максимальную скорость движения тела (s—в метрах, /—в секундах). 50. Закон движения тела, брошенного вертикально вверх, задан уравнением s = vot—0,5gt2. Найдите наибольшую высоту подъема тела. 51. Закон движения тела, брошенного вертикально вверх, задан уравнением s= 19,6f—4,9f2. Найдите наибольшую высоту подъема тела (s—в метрах, t—в секундах). § 6. НАПРАВЛЕНИЕ ВЫПУКЛОСТИ ГРАФИКА ФУНКЦИИ Кривая y=f (х) называется выпуклой вниз в промежутке а<х<Ь, если она лежит выше касательной в любой точке этого промежутка (рис. 33, а). Кривая y=f(x) называется выпуклой вверх в промежутке а<х<Ь, если она лежит ниже касательной в любой точке этого промежутка (рис. 33,6). Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции. Выпуклость вниз или вверх кривой, являющейся графиком функции y=f (jc), характеризуется знаком ее второй производной: если в некотором промежутке /" (jc) > 0, то кривая выпукла вниз в этом промежутке; если же /"(*)< 0, то кривая выпукла вверх в этом промежутке. ) 52. О Находим /'(*) = — Х/х2,/" (х) = 2/х3. Подставляя во вторую производную значения Xi = —2 и х2 = 1, получим /"(—2) = 2/(—2)3<0, /"(1) = 2/1 >0. Таким образом, в точке х=—2 кривая выпукла вверх, а в точке х=1— выпукла вниз, ф 53. Найти промежутки выпуклости кривых: 1) /{х) = хъ\ 2) /(х) = х4 — 2х3 + 6х—4.
Находим /'(х) = 3х2,/" (х) = 6х. В промежутке — оо<х<0 имеем т. е. в этом промежутке кривая выпукла вверх; в промежутке имеем /" (х) > 0, т. е. в этом промежутке кривая выпукла вниз 2) 54. Исследуйте на направление выпуклости кривые: 1) у — — 1/х в точках Xi = — 1 и х2 = 1; 2) у= 1/х2 в точках xi = —2 и х2=1. Найдите промежутки выпуклости кривых: 55. 1) у = 2х3; 2) >; = х2; 3).у=-х2-1; 4) у = х2 + Зх—1. 56. 1) у = х3-6х2 + 2х—6; 2) >> = х4 —2х3 —12х2 + 24х + 8. § 7. ТОЧКИ ПЕРЕГИБА Точка графика функции y—f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба. Точками перегиба могут служить только критические точки, принадлежащие области определения функции y—f (х), в которых вторая производная /" (х) обращается в нуль или терпит разрыв. Если при переходе через критическую точку х0 вторая производная /" (х) меняет знак, то график функции имеет точку перегиба (х0; / (х0)). Пр авило нахождения точек перегиба графика функции y—f{x) I. Найти вторую производную f"(x). И. Найти критические точки функции y=f(x), в которых /" (х) обращается в нуль или терпит разрыв. III. Исследовать знак второй производной /"([11]) в промежутках, на которые найденные критические точки делят область определения функции / (х). Если при этом критическая точка х0 разделяет промежутки выпуклости противоположных направлений, то х0 является абсциссой точки перегиба функции^ IV. Вычислить значения функции в точках перегиба. 57. Найти точки перегиба кривых: \)f{x)=bx2-x\ 2)f(x)=x+*/P'-2. О 1) Находим /' (х)= 12х—Зх2, /" (х) = 12 —6х. Полагая /" (х)=0, получим единственную критическую точку х=2. Так как в промежутке — оо<х<2 имеем /" (х)>0, а в промежутке 2<х<оо имеем /"(х)<0, то при х=2 кривая имеет точку перегиба. Найдем ординату этой точки: /(2)= 16. Итак, (2; 16)—точка перегиба. Находим /' (х)= 1 + - \fx*, f ,(х)=—' —7=* Здесь критической явля- 3 9 \/х ется точка х=0, в которой вторая производная терпит разрыв. Очевидно, что /"(х)<0 в промежутке — оо<х<0 и /" (х)>0 в промежутке 0<х<оо, т. е. кривая при х=0 имеет точку перегиба (0; —2). ф Найдите точки перегиба следующих кривых: 58. 1) f (х) = х3 —х; 2) >^=^x3 —Зд:2 + 8д:—4. 59. 1)/(jc)=jc4-10jc3 + 36jc2-100; 2) f(x)=x4 — 8д:3 + 18л:2—48x + 31; 3) /(х)=д:4 —6д:34-12л:2—10. 60. 1)f(x)=xe-x; 2) f(x) = e~x\ § 8. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ Общая схема построения графиков функций I. Найти область определения функции. II. Выяснить, не является ли функция четной, нечетной или периодической*. III. Найти точки пересечения графика с осями координат (если это не вызывает затруднений). IV. Найти асимптоты графика функции. V. Найти промежутки монотонности функции и ее экстремумы. VI. Найти промежутки выпуклости графика функции и точки перегиба. VII. Построить график, используя полученные результаты исследования. 61. О 1. Функция определена на всей числовой прямой, т. е. Z>(y) = R. 2. Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической. 3. Найдем точку пересечения графика с осью Оу: полагая х=0, получим у=—Ъ. Точки 35 пересечения графика с осью Ох в данном случае найти затруднительно. 4. Очевидно, что график функции не имеет асимптот. 5. Найдем производную: у' — Ъх2— 12х+9. Далее, имеем (Зх2— 12x4-9 = Г * = =0)о(х2 — 4х4~3=0)оI ’ Точки х= 1 и х=3 делят область определения |_х = 3. функции на три промежутка: —оо<х<1, 1<х<3 и 3<х<оо. В промежутках — оо<х<1 и 3<х<оо j>'>0, т. е. функция возрастает, а в промежутке 1<х<3 /<0, т. е. функция убывает. При переходе через точку х=1 производная меняет знак с плюса на минус, а при переходе через точку х=3—с минуса на плюс. Значит, утах=у(1)= 1, утт=у(3)= — 3. 6. Найдем вторую производную: у" = 6х—12; 6х—12 = 0, х=2. Точка х=2 делит область определения функции на два промежутка — оо<х<2 и 2<х<оо. В первом из них j>"<0, а во втором /'>0, т. е. в промежутке — оо<х<2 кривая выпукла вверх, а в промежутке 2<х<оо выпукла вниз. Таким образом, получаем точку перегиба (2; —1). 7. Используя полученные данные, строим искомый график (рис. 35). # X2' 62. Построить график функции У——у — оо <х<3 О 1. Находим область определения функции: D(y)=\ |_3<х< оо. 2. Данная функция не является ни четной, ни нечетной, ни периодической. 3. При х=0 получим j=0, т. е. график проходит через начало координат. 4. Так как lim /(х)=± оо, то прямая х=3 служит вертикальной *-»3±0 асимптотой графика. Далее находим: *= lim f-^= lim -^-r=l, Jt->±oo * jc ± oo X (x 3) Г x2 1 3x b= lim [/(x)—kx] = lim —x 1= lim -=3. jt-*±oo x-»±oo|_^ — 3 J x-* + oo X — 3 Следовательно, прямая у=х+Ъ является наклонной асимптотой графика. 5. Находим 2х(х—3) — х2 х2 —6х х(х—6) у рПр =(^=(^ГЗ)Т- Производная у' обращается в нуль в точках х=0 и х = 6 и терпит разрыв при х=Ъ. Этими точками числовая прямая делится на четыре промежутка: — oo<x<0, О <л:<3, 3<лг<6 и 6 <х<оо. Исследуем знак у' в каждом из них; очевидно, что />0 в промежутках — оосхсО и 6<х<оо (в этих промежутках функция возрастает) и у'<0 в промежутках ОсжЗ и 3 <х<6 (в этих промежутках функция убывает). При переходе через точку х=0 производная меняет знак с плюса на минус, т. е. это точка максимума, а при переходе через х = 6—с минуса на плюс, т. е. это точка минимума. Находим Утах ~У (0) = 0, Ут'т ~У (6) = 12. 6.
(*-3)4 =
Вторая производная в нуль нигде не обращается и терпит разрыв при х = Ъ. В промежутке — oo<x<3 имеем у"< 0, т. е. в этом промежутке кривая выпукла вверх; в промежутке 3<х<оо имеем у">0, т. е. в этом промежутке кривая выпукла вниз. Точек перегиба нет. 7. На основании полученных данных строим график функции (рис. 36). ф Исследуйте следующие функции и постройте их графики: 63. 1) у—2х2 — 8лг; 2) у=— Зх2+\2х; 3) у=х2 + 5х+4; 4) у= = — х 2 + 2х +15. 64. \) у = ^х3 — 9; 2) у = х3 — Зх; 3) у=Зх3—х; 4) у=— х3+х. 65. 1) у=-х4; 2) у=-$х5. 66. 1) у = х3 + 6х2 + 9л:+8; 2) у = 2х3 — Зд:2— 12л:— 1; 3) у=х3 — 6х2+16; 4) ^ = 2лг3 + Зх2—12х—10. 67. 1) у = х4-5х2+4; 2) у= -х4 + 8х2 + 9. 68. 1) у=^\ 2) у=- 1
1 х2 — 7х+\2 з 6-х 3 71. х —I 72. 1) у=х—у/х; 2) у=х2 у/х— 3. 73. 1) j=ln(x2 + l); 2) у=х In*. 74. 1) у=311х; 2) у=е~х\ 75. 1) у=(х-\)ех; 2) у=х2е~х. ЗАЧЕТНАЯ РАБОТА
I вариант 1) Найдите промежутки монотонности функции _у= —-х34--х24-1. 2) Найдите наименьшее и наибольшее значения функции '=з*3+ 4- -х2 —2х— - на отрезке — 2<х<2. 3) Найдите промежутки выпуклости и точки перегиба кривых: а) у=х3 + Зх2; б) >>=^х3—4х. 4) Дан закон прямолинейного 1 з 1 2 1 движения точки s= — г + -t + -/4- 5 2 2 + 1 (/ — в секундах, s—в метрах). Найдите максимальную скорость движения этой точки. II вариант 1) Найдите промежутки монотонности функции у = х4—4x4-4. 2) Найдите наименьшее и наибольшее значения функции у=-х3 + 4-*2 — Зх—4 на отрезке —4<х<2. 3) Найдите промежутки выпуклости и точки перегиба кривых: а) у=хг — 12х24-145; б) _у=^х34- 2 1 + х + 4) Дан закон прямолинейного движения точки s= — -t3 + 3t2 + 5t+3 (t—в секундах, s—в метрах). Найдите максимальную скорость движения этой точки.
Глава 9 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ § 1. РАДИАННОЕ ИЗМЕРЕНИЕ ДУГ И УГЛОВ 1. Основные формулы, связанные с радианным измерением дуг. При радиан- ном измерении дуг (и соответствующих им центральных углов) за единицу измерения принимается радиан—дуга, длина которой равна радиусу этой дуги. Радианная мера дуги вычисляется по формуле я=//Д, (9.1) где а—радианная мера дуги; /—длина дуги окружности; R—радиус этой дуги. Формула перехода от градусного измерения к радианному имеет вид a=(7i/180°) а, (9.2) где а—градусная мера дуги (угла). Радианная мера 1° равна 0,0175 рад. Формула перехода от радианного измерения к градусному имеет вид а=(180°/я) • я. (9.3) Градусная мера 1 рад равна 57°17'44",8«57°,3. Длина дуги окружности равна радианной мере дуги, умноженной на радиус этой дуги: Площадь кругового сектора равна половине радианной меры дуги сектора, умноженной на квадрат радиуса круга: S"IT=“R21 2- (9.5) 2. Основные понятия, связанные с вращательным движением точки. При вращательном движении твердого тела вокруг неподвижной оси различают две скорости: линейную и угловую. Скорость любой точки твердого тела во вращательном движении называется линейной скоростью. Линейная скорость v точки при равномерном движении по окружности радиуса R вычисляется по формуле v=2nR/T, (9.6) где Г—период вращения, т. е. время (в секундах), за которое совершается один; полный оборот точки. Угол, на который поворачивается радиус любой точки равномерно вращающегося твердого тела за одну секунду, называется угловой скоростью. Угловая скорость выражается в радианах в секунду (рад/с). Зависимость между угловой скоростью со и периодом вращения Т выражается формулой (о=2п/Т. (9.7) Линейная скорость v точки, находящейся на расстоянии R от оси вращения, и ее угловая скорость связаны соотношением v = (oR. (9.8) При неравномерном вращении твердого тела его угловой скоростью со называется скорость изменения угла ф за время t. Угловая скорость (рад/с) в этом случае есть производная угла поворота ф по времени t: dtp ш=—.. (9.9) dt Угловое ускорение 8 (рад/с2) есть производная от угловой скорости со по времени t: d со 8=—. (9.10) dt 1. Чему равна точная радианная мера дуг: 1) 240°; 2) 300°? О По формуле (9.2) получим: 1) а=(п/\ 80°) • 240°=4я/3; 2) а=(л:/180°) • 300° = 5тс/3. • 2. Чему равна точная градусная мера дуг: 1) 7я/6; 2) 5я/4? О По формуле (9.3) получим: 1) а=(180°/я) • (7я/б) = 210°; 2) а=(180°/я)-(5я/4) = 225°. • 3. Колесо, радиус которого равен 0,65 м, повернулось на угол 4 рад. Найти длину пути, пр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.014 с.) |






 Имеем /'(х)=3х2 —12х,(3;с2 —12х=0)<^* Составим таблицу:
Имеем /'(х)=3х2 —12х,(3;с2 —12х=0)<^* Составим таблицу:
 -оо <лг<0
-оо <лг<0 /'(*)
/'(*) положителен, то знак этой дроби совпадает со знаком ее числителя. Учитывая, что функция определена при O^x^l, получаем: у'>0, при 1—2х>0, т. е. при 0<jc< 1 /2; у'<0 при 1— 2х<0, т. е при l/2<x<L
положителен, то знак этой дроби совпадает со знаком ее числителя. Учитывая, что функция определена при O^x^l, получаем: у'>0, при 1—2х>0, т. е. при 0<jc< 1 /2; у'<0 при 1— 2х<0, т. е при l/2<x<L О 1) Находим /'(*) = 2х—4. Полагая /' (х)=0, получим единственную критическую точку х=2. Дальнейшие рассуждения представлены в таблице:
О 1) Находим /'(*) = 2х—4. Полагая /' (х)=0, получим единственную критическую точку х=2. Дальнейшие рассуждения представлены в таблице: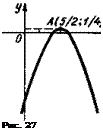 2) Находим f (х)= — 2х+5; (— 2л;+5 = 0)о(л:=5/2). Составим таблицу:
2) Находим f (х)= — 2х+5; (— 2л;+5 = 0)о(л:=5/2). Составим таблицу: О 1) Находим f (х) = 2хъ\ (2л:3 = 0)<?>(л:=0). Составим таблицу:
О 1) Находим f (х) = 2хъ\ (2л:3 = 0)<?>(л:=0). Составим таблицу:
 , г-тг 2(х— 5) +3х 5 х—2
, г-тг 2(х— 5) +3х 5 х—2
 У\
У\ сравнить полученные значения; тогда наименьшее и наибольшее из них являются соответственно наименьшим и наибольшим значениями функции в рассматриваемом промежутке.
сравнить полученные значения; тогда наименьшее и наибольшее из них являются соответственно наименьшим и наибольшим значениями функции в рассматриваемом промежутке. -xj=^x-x 2
-xj=^x-x 2



 На какой высоте h надо повесить фонарь над центром круговой площадки радиуса а, чтобы площадка была макси-
На какой высоте h надо повесить фонарь над центром круговой площадки радиуса а, чтобы площадка была макси-


 (h2+a2)3>2-j(h2+a2)1'2-2h-h
(h2+a2)3>2-j(h2+a2)1'2-2h-h

 Исследовать на направление выпуклости кривую / (х) = 1 /х в точках xi = —2 и *2 = 1.
Исследовать на направление выпуклости кривую / (х) = 1 /х в точках xi = —2 и *2 = 1. Находим /'(*) =4х3 —6х2 + 6, f" (х) = = 12х2 —12х= 12х(х—1). Очевидно, что в промежутках — оо<х<0и1<х<оо выполняется неравенство/" (х)> 0, т. е. в этих промежутках кривая выпукла вниз, а в промежутке 0<х<1 имеет место неравенство /" (х) < 0, т. е. в этом промежутке кривая выпукла вверх, ф
Находим /'(*) =4х3 —6х2 + 6, f" (х) = = 12х2 —12х= 12х(х—1). Очевидно, что в промежутках — оо<х<0и1<х<оо выполняется неравенство/" (х)> 0, т. е. в этих промежутках кривая выпукла вниз, а в промежутке 0<х<1 имеет место неравенство /" (х) < 0, т. е. в этом промежутке кривая выпукла вверх, ф Построить график функции у = х3 — — 6л:2 + 9л:—3.
Построить график функции у = х3 — — 6л:2 + 9л:—3. Находим
Находим (2х—6)(х—З)2 — 2(х—3) (х2 — 6л:)
(2х—6)(х—З)2 — 2(х—3) (х2 — 6л:)

 1-х2' х2—4
1-х2' х2—4 • 2) J_(x+1)(jc+8)
• 2) J_(x+1)(jc+8) 1) у =
1) у =


