
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измените порядок интегри- и х—4.Содержание книги
Поиск на нашем сайте
3) - - 2 4 з^ + з fdy J /(•*> у) dx. 1 1 у § 4. ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ Преобразование двойного интеграла от прямоугольных координат х и у к полярным г и ф (см. гл. 14, § 1) выполняется по формуле >/) =JJy(r e°s Ф, r sin tp)r dr d<p, (29.10) D D где x=rcosq>, y—rsinф, rdrdq> = dS—дифференциал площади. Вычисление двойного интеграла в полярных координатах сводится к вычислению повторного интеграла по г и ф в заданной области D. Если область D (рис. 208) ограничена лучами, образующими с полярной ОСЬЮ углы ф! И ф2, И кривыми Г = гДф) И Г = Г2 (ф) (где Ф1<Ф2, г1<г2), то двойной интеграл вычисляется^по формуле ИЛ*> y)dxdy= J d(p J f(r cos ф, r sin ф) r dr. (29. 11) D 9l ^(ф) Если область D ограничена линией r=r (ф) и начало координат лежит внутри области D (рис. 209), то
26. Вычислить двойной интеграл jjrsincprfrtftp, если область D
Я а jjrsin<pdr*/<p= J Jrsin<prfr. D я/2 0 Вычислим внутренний интеграл, считая sincp постоянным: Г • л Гг2 • Т *2 •
а2 С а2г а2 а2 — sin9^=-T[cos9]'2=-—(-1-0)=—. • Я/2 27. Преобразовать к полярным координатам и вычислить двойной интеграл Я (x+y)dxdy, если область D ограничена D линиями х2+у2=1, х2+у2 = 49 у^О. О Построим область D (рис. 211). Применив формулы перехода к полярным координатам, получим x=r coscp, >>=г sin ср; тогда JJ (x+y)dxdy=\]{r cos ф+z sin ф) г dr dtp. D D Область D в полярной системе координат запишем в виде системы неравенств О^ф^тг, 1^г<2. Поэтому Я, 2 JJ (x+y)dxdy=\dy\ г2 (cos ф + sin ф) dr. D о 1 Вычислим внутренний интеграл, считая совф + втф постоянным: J г2 (cos ф 4- sin ф) dr=(cos ф + sin ф) J = (cos ф + sin ф)0—^^ (cos ф + sin ф). Вычислим внешний интеграл: 28. Преобразовать к полярным коорди- натам и вычислить двойной интеграл
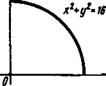
D частью окружности х2+у2 = \6, х^О, у>0. О Построим область D (рис. 212). Полагая x=rcoscp, y=rsin<p, получим у/х2 +у2=у/г2 cos2<p + г2 sin2<p = =у/г2 (cos2 ф + sin2 ф)=г. Область D в полярных координатах определяется системой неравенств 0<ф<71/2, О^г^ф. Согласно формуле (29.11), находим Я/2 4 я/2 4 JJ 'y/xF+у2dxdy= j* dy^rrdr= J dy Jr2</r= 0 0
=4 # 0 0 29. Вычислите повторные интегралы: 2я 2 а я/2 6 я 3 1) J Лр J г2?Йг; 2) j dy\r2 cosy dr; 3) \dy J г2 sin ф dr; 0 0 я/6 3 0 1 я/3 2 я/6 2 cos ф 4) j d<p $ г3 cosy dr; 5) J dy J r cosy dr. 1 ~ я/6 2 30. Вычислите двойные интегралы: 1) \\r2dydr, D—область, ограниченная окружностями г=1 и D г=3; 2) Jjr3flfcpdr, область D задана системой неравенств я/4^ф<я/3, D 2<г<4; 3) {j sin 2фй?ф dr, область D задана системой неравенств D я/6<ф<я/2, 1<г<3. 31. круговое кольцо между окружностями х +
dxdy, D—область, ограниченная окруж-
ностью х2+у2^\6.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.161.43 (0.007 с.) |

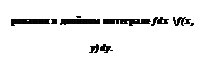 Измените порядок интегрирования в двойном интеграле
Измените порядок интегрирования в двойном интеграле ИЛ*> y)dxdy=$2ond(?\ оФ> Лг cos ф, г sin ф) г dr.
ИЛ*> y)dxdy=$2ond(?\ оФ> Лг cos ф, г sin ф) г dr.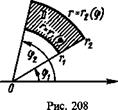 D—круговой сектор, ограниченный линиями г=а, ф = тс/2 и ф = я.
D—круговой сектор, ограниченный линиями г=а, ф = тс/2 и ф = я.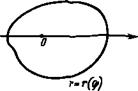
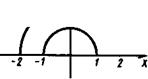 Рис. 211
Рис. 211
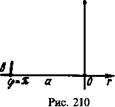 О Построим сектор ОАВ с центром в полюсе О (рис. 210). Имеем повторный интеграл
О Построим сектор ОАВ с центром в полюсе О (рис. 210). Имеем повторный интеграл Jrsincpdr= ysm<p =—вшф.
Jrsincpdr= ysm<p =—вшф.
 Я ->/x2+y2dxdy, если область D ограничена
Я ->/x2+y2dxdy, если область D ограничена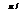 я/2
я/2 Вычислите двойные интегралы, предварительно преобразовав их к полярным координатам:
Вычислите двойные интегралы, предварительно преобразовав их к полярным координатам: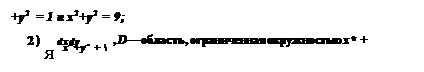
 D
D


