
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательная и нормаль к кривойСодержание книги
Поиск на нашем сайте
Пусть на кривой y=f(x) дана точка М0(х0; у0), для которой y0=f(x0) (рис. 149). Значение производной функции y=f(x) при х=х0 равно угловому коэффициенту касательной, проведенной к кривой y—f{x) в ее точке с абсциссой х0, т. е. k=y'(xo)=f'(xo)=4*> где а—угол между касательной к кривой в точке М0(х0; у0) и положительным направлением оси Ох. Уравнение касательной к кривой y=f(x) в точке М0 (х0; у о) имеет вид У-Уо=ГМ(х-х0). (19.25) Нормалью к кривой y=f(x) в данной ее точке М0(х0; у0) называется перпендикуляр к касательной, проведенной через точку касания М0(х0; у0) (рис. 149). Уравнение нормали к кривой y=f(x) в точке М0(х0; у0) имеет вид у-у =- I (х-х0). (19.26) / (*о) У'
Направление кривой в каждой ее точке определяется направлением касательной к ней в этой точке, поэтому для нахождения угла наклона кривой в данной ее точке надо вычислить угол между касательной, проведенной в этой точке, и осью Ох. Углом между пересекающимися прямой и кривой называется угол между прямой и касательной к кривой, проведенной через точку их пересечения (рис. 150). Углом между двумя пересекающимися кривыми называется угол между касательными к этим кривым, проведенным в точке их пересечения (рис. 151). 122. Найти угол наклона к оси Охкасательной, проведенной к кривой у = sinx в точке х=п/3. О Найдем производную функции у = sinx при х=п/3: У=cosx, у' (к/3)=cos (тс/3) = 1/2. Тангенс угла наклона касательной в точке х=п/3 равен 1/2, т. е. fc=tgoc=l/2, откуда a=arctg (1/2) «26°,6 (рис. 152). ф 123. Под какими углами парабола у = х2+хпересекает ось Ох? О Найдем точки пересечения параболы у=х2 + х с осью Ох. Для этого решим систему уравнений Гу=х2 + х, |”(—1; 0), \у=0 *1(0; 0).
о Значит, парабола пересекает ось Ох в точках Л(—1;0) и 0(0; 0) (рис. 153). Найдем угловые коэффициенты касательных к параболе в этих точках: /=(*2+*)' = 2*+1; £(—1)=2 (—1)+1 = — 1; *(0) = 2-0 + 1 = 1. Вычислим углы ах и а2, образуемые касательными в точках пересечения параболы с осью Ox: tgax = — 1, ^ = 135°; tga2 = l, a2=45°. • 124. Найти угол, образованный кривой у=\пх при пересечении ее с осью Ох. О Найдем точку пересечения кривой у=\пх с осью Ох. В этой точке 1пх=0, откуда х= 1 (рис. 154). Вычислим угловой коэффициент касательной в точке jc= 1: у'=(\пх)' = 1/х; /(1)=1. Найдем угол, образуемый касательной в точке пересечения кривой у—\пх с осью Ox: tga=l, a=45°. ф 125. К параболе у=3х2 —х в точке jc= — 1 проведены касательная и нормаль. Составить их уравнения. О Для составления уравнения касательной найдем ординату точки М, через которую проходит касательная, и ее угловой коэффициент. Найдем ординату точки касания, подставив в уравнение параболы значение х= — 1: ,(-1)=3-(-1)2-(-1)=4; М(-1;4). Вычислим угловые коэффициенты касательной и нормали: к„,с=у'={Зх2-хУ = 6х-1; /(—1)=6 (—1)—1 = —7; кялрн = 1р. Подставив в уравнения (19.25) и (19.26) координаты точки М и значения £кас и кнорм, получим у—4= — 7(хН-1), или 7x+j+3=0 (уравнение касательной) и у—4=^(х+1), или х—7у+29 = 0 (уравнение нормали), ф 126. Составить уравнение касательной и нормали к эллипсу х2/21+у2/24=\ в точке (—3; —4). О Дифференцируем уравнение эллипса по х, рассматривая у как функцию от х: Ф 2х 2уу' Л п Л Л 8л: —+—=0, 8х+9уу = 0, откуда у =-—. 27 24 9у Найдем угловые коэффициенты касательной и нормали в точке (-3; —4); * 3)- 8MI- 2» -2 *ac У \ 9 (—4) 3’ рм 2 Отсюда получаем у+4= — (2/3)(х+3), или 2х+37+18=0 (уравнение касательной) и 7+4=(3/2)(х+3), или Зх—27+1=0 (уравнение нормали), ф 127. На параболе у=х2—2х—8 найти точку М, в которой касательная параллельна прямой 4х+7+4=0. О Определим угловой коэффициент касательной к параболе: к=у' = = (х2 — 2х—8)' = 2х—2. Найдем угловой коэффициент данной прямой: 4jc+7+4=0; у= — 4х—4; /:= — 4. Касательная к параболе и данная прямая параллельны, следовательно, их угловые коэффициенты равны: 2х—2= — 4, откуда абсцисса точки касания х = — 1. Ординату точки касания М вычислим из уравнения параболы: 7(1) = (-1)2-2 (—1)—8=—5; М(—1; —5) (рис. 155). * 128. Вычислить острые углы, образуемые при пересечении параболы х2—4у = 0 и прямой х—27+4=0. О Найдем точки пересечения параболы и прямой; для этого решим
х2—47=0, Г(~~2; 1), 2 +4 ' 0Н (4- 4) * ^аким °бРазом’ парабола и прямая пересекаются в точках А(—2; 1) и В (4; 4) (рис. 156). Найдем угловой коэффициент данцой прямой: х—2у+4=0; у=(1 /2) х+2, к =1/2. Вычислим угловые коэффициенты касательных в точках А (—2; 1) и
Угол между параболой и прямой в точке А найдем как угол между двумя прямыми с угловыми коэффициентами kl= — 1 (угловой коэффициент касательной в точке А) и к2 = 1/2 (угловой коэффициент прямой): 1/2-(~1} =3; Ф1«7ГД 8Vl 1 +k2k1 1+(1/2)(—1) Vl Аналогично находим угол между параболой и прямой в точке В: 2-1/2 3 tg<P2 =,, „,-,4=7; ф2~3б°,9. •
129. Вычислить острые углы, образуемые при пересечении парабол у2 = 4х и х2=у/2. О Найдем точки пересечения парабол; для этого решим систему уравнений
Следовательно, параболы пересекаются в точках 0(0; 0) и А (1; 2) (рис. 157). Угол между двумя пересекающимися параболами найдем как угол между касательными к ним, проведенными в точке пересечения. Вычислим угловые коэффициенты касательных к параболам в точках их пересечения. В точке (0; 0) касательными к параболам служат оси Ох и Оу, следовательно, в этой точке параболы пересекаются под прямым углом. Для нахождения углового коэффициента касательной к параболе у2=4х в точке А перепишем ее уравнение в виде у=2 у/х (перед радикалом берем знак плюс, так как пересечение парабол происходит в I четверти): к=у'=\1у/х; к=у’(1) = 1. Вычислим угловой коэффициент касательной к параболе х2—у/2 в точке А; записав ее уравнение в виде у = 2х2, имеем к=у'=4х; к=у’ (1)=4 • 1 —4. Найдем угол ф между касательными, зная их угловые коэффициенты 130. Найдите угловой коэффициент касательной, проведенной к параболе: 1) у= -х2-\-х в точке х=— 2; 2)у=х2 — Зх+2 в точке х=3. 131. Найдите угол наклона к оси Ох касательной, проведенной к кривой: 1) у=х2—2х в точке х — 2; 2) у=х3 в точке х= —2; 3) 7=sin;c в точке х=2п/3; 4)>>=tgx в точках х=я/3, х=п/4. 132. Под какими углами парабола у=х2+2х—8 пересекает ось 0x1 133. Найдите угол, образованный кривой у=sinx при пересечении ее с осью Ох в точке 1) х=0; 2) х=к. 134. Под каким углом: 1) кривая у=Igx пересекает ось Ох; кривая у=е'/з* пересекает ось Оу1 135. Составьте уравнения касательной и нормали: 1) к параболе 7=х2 — 7х+10 в точке х = 4; 2) к кривой у=2х3 в точке х= — 1. 136. Составьте уравнения касательной и нормали: 1) к окружности х2+у2 = 25 в точке (—3; 4); 2) к эллипсу х2/100+72/25 = 1 в точке (—8; 3); 3) к гиперболе х2/16—у2/64= 1 в точке (—5; 6); 4) к параболе у2 = 8х в точке (2; —4); 137. Составьте уравнение касательной и нормали к кривой: 7 = sin3x в точке (я/3; 0); 2) у = sin (х/3) в точке (я; >/3/2); 1) 7=cos3x в точке (я/6; 0). 138. Найдите координаты точки, в которой касательная к параболе y = x2-h3x—10 образует угол 135° с осью Ох. 139. Найдите координаты точки, в которой касательная к кривой 7=sinx (0<х<я/2) образует угол arctg(^/3/2) с осью Ох. 140. На параболе у=— х2 + 7х—10 найдите точку, в которой касательная параллельна прямой х+у—1=0. 141. В какой точке касательная к параболе 7= — х2 +4 перпендикулярна прямой х—2у + 2 = 0? 142. Вычислите острые углы, образуемые при пересечении параболы у2—х=0 с прямой х+у—6 = 0. 143. Вычислите острые углы, образуемые при пересечении парабол: 1)7 = х2 и х=у2; 2)у2 = 4х и 2х2 = 21у. 144. Вычислите острый угол, образованный при пересечении кривой у = lgx и прямой 7=1. § 8. СМЕШАННЫЕ ЗАДАЧИ 145. Через центры окружностей х2+72—12х—67+29 = 0 и х2 + +у2+4х+6у+4 = 0 проведена прямая до пересечения с осью Ох. Вычислите угол, образуемый этой прямой с осью Ох. 146. Найдите угол между прямыми, проходящими через центр окружности х2+у2 — 4х—167 + 32 = 0 и через фокусы эллипса х2/36 + +72/20 = 1. 147. Вычислите углы, под которыми видны из центра окружности х2+у2 — 6х—12^+36=0 большая и малая оси эллипса х2/36 + +72/16=1. 148. Окружность х2 + у2 + 2х—6у—40 = 0 пересекает прямая Зх—7+16 = 0, внутренний отрезок которой служит стороной вписанного в окружность прямоугольника. Составьте уравнения сторон этого прямоугольника. 149. Найдите точки пересечения эллипса х2/8+72/2=1 и окружности х2+72 = 5. 150. В окружность х2+72 = 4 вписан правильный треугольник, одна из вершин которого имеет координаты (0; 2). Вычислите координаты двух других вершин треугольника. 151. Составьте уравнения прямых, проходящих через фокусы эллипсов х2/25 +72/16 = 1 и х2/24+72/49= 1. 152. Вычислите площадь квадрата, вписанного в эллипс х2/36 + +72/9= 1. 153. Вычислите площадь прямоугольника, вписанного в эллипс х[32]/16+у2/12 = 1 так, что две его противоположные стороны проходят через фокусы. 154. Составьте уравнение гиперболы, вершины которой находятся в фокусах эллипса x2/20+}>2/8 = 1, а фокусы—в вершинах эллипса. 155. Найдите расстояние от вершины гиперболы jc2/25—4jp2/25 = = 1 до ее асимптоты. 156. Составьте уравнение эллипса, фокусы которого находятся в фокусах равносторонней гиперболы х2—у2=\$, если эллипс проходит через точку (5^2; Ау/2). 157. Найдите точки пересечения двух парабол, имеющих общую вершину в начале координат, а фокусы—в точках Fl (3; 0) и f2(0; з/8). 158. Окружность х2+у2 = 20 пересекает параболу х2 = 8у. Составьте уравнение их общей хорды. 159. Из точки О под острым углом к горизонту брошено тело, которое, описав дугу параболы, упало на землю на расстоянии 40 м от точки О. Найдите параметр параболической траектории, если максимальная высота, достигнутая телом, равна 25 м (сопротивление воздуха в расчет не принимать). ЗАЧЕТНАЯ РАБОТА
I вариант 1) Составьте уравнение радиуса, проведенного в точку А(—3; 1) окружности: х2+у2—4х+2у—24=0. 2) Составьте уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно 20, а эксцентриситет равен 5/6. 3) Дана гипербола jc2/81 — —у2/63=1. Найдите ее эксцентриситет. 4) Дана парабола у2 — 2у +16х+ + 65 = 0. Составьте уравнение ее оси. 5) Дана парабола х2 + 6х—\2у— 3 = 0. Составьте уравнение ее директрисы. II вариант 1) Составьте уравнение касательной, проведенной в точке А(—2; 1) окружности х2+у2 — 2х+ +4у—13=0. 2) Дан эллипс х2/625+>>2/400= 1. Найдите его эксцентриситет. 3) Составьте уравнение гиперболы с фокусами на оси Ох, зная расстояние между фокусами 2с=90 и уравнения ее асимптот у=±(4/3)х. 4) Дана парабола x2 + 6x+20y— 51=0. Составьте уравнение ее оси. 5) Дана парабола у2 + Ъу+2Ъх+ + 72=0. Составьте уравнение ее директрисы.
Глава 20 ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ § 1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 1. Простейшие задачи на построение сечения многогранника. Сечением многогранника называется часть секущей плоскости, ограниченной линиями пересечения этой плоскости с поверхностью многогранника. При постро- ении сечения многогранника необходимо найти: 1) положение секущей плоскости; 2) линию пересечения секущей плоскости с поверхностью многогранника. 1. О Плоскость, проходящую через точки К, L, М, обозначим а. Плоскость а имеет с плоскостью SAB общие точки К и L; поэтому плоскости SAB и а пересекаются по прямой KL. Отрезок KL—пересечение грани SAB и плоскости а. Аналогично построим отрезок КМ. Плоскость грани АВС имеет с секущей плоскостью а общую точку М; для построения линии пересечения этих плоскостей достаточно найти еще одну их общую точку. Такой точкой является точка D пересечения прямых KL и АВ (точка D лежит в плоскости айв плоскости АВС). Проведя прямую MD, получим точку N на ребре ВС. Отрезки MN и NL—две другие стороны сечения. Итак, сечение MKLN—искомое. # 2. Даны тетраэдр SABC и точки М и N, причем точка М лежит на ребре SC, а точка N—на ребре АВ. Постройте пересечение плоскостей АВМ и SCN. 3. Дан куб ABCDA^B^C^D^ причем К лежит на ребре ААи L—на ребре ССг и М—на ребре DC. Постройте сечение куба плоскостью, проходящей через точки К, L, М. 4. В кубе ABCDA1BlClD1 постройте сечение плоскостью, проходящей через: 1) вершины Л19 В и D; 2) середины ребер, выходящих из одной вершины; 3) диагональ основания BD и вершину Ах; 4) три точки, лежащие на ребрах ААи ССХ и ВС. 5. В тетраэдре SABC постройте сечение плоскостью, проходящей через три точки, лежащие на ребрах SA, АС и ВС. 6. В тетраэдре SABC постройте сечение плоскостью, проходящей через вершину S и точки М и N, лежащие соответственно на ребрах АВ и АС. 7. Постройте сечение тетраэдра SABC плоскостью, проходящей через вершину А и середины ребер BS и CS. Найдите площадь сечения, если ребро тетраэдра равно а. 8. Постройте сечение тетраэдра SABC плоскостью, проходящей через ребро SA и точку пересечения медиан грани АС В. Найдите площадь сечения, если ребро тетраэдра равно а. 9. На модели куба укажите его ребра, лежащие на скрещивающихся прямых. 10. 11. Сколько пар ребер, лежащих на скрещивающихся прямых, имеет тетраэдр? 12. Найдите расстояние между скрещивающимися диагоналями двух соседних граней куба с ребром а. 3. Параллельные прямые 13. Концы данного отрезка длиной 50 см отстоят от плоскости на 30 и 44 см. Найдите проекцию этого отрезка на плоскость. 14. Отрезок длиной 15 см пересекает плоскость, концы его отстоят от плоскости на 3 и 6 см. Найдите проекцию этого отрезка на плоскость. 15. Отрезок пересекает плоскость; концы его отстоят от плоскости на 3 и 12 см. Найдите расстояние середины этого отрезка от плоскости. 4. Параллельность прямой и плоскости 16. Дан тетраэдр SABC, причем М лежит на ребре AS и TV на ребре АС. Построить сечение тетраэдра плоскостью, проходящей через точки М и N и параллельной прямой АВ. О Анализ. Предположим, что сечение построено (рис. 160). Пересечение плоскости сечения с гранью ASC получим, соединив точки М и N. По условию, прямая АВ параллельна плоскости сечения, поэтому грани АВС и ABS пересекают плоскость сечения по отрезкам PN и MQ, параллельным прямой АВ. Построение. 1) NP\\AB, Р лежит на ребре ВС; 2) MQ\\AB, Q лежит на ребре SB. Четырехугольник NMQP—искомое сечение. Доказательство. Плоскость NMQP параллельна прямой АВ, так как MQ\\AB. Исследование. Задача имеет единственное решение, так как ребро ВС пересекает плоскость сечения в единственной точке Р и через точки М, N, Р проходит единственная плоскость. Мы применили общую схему решения задач на построение (анализ, построение, доказательство, исследование). 17. 1) Даны точка А и прямая а, причем А не лежит на прямой а. Проведите через точку А прямую, параллельную данной плоскости. 2) Даны точка А и прямая а, причем А не лежит на прямой а. Проведите через точку А плоскость, параллельную прямой а. 18. Дано а\\Ь. Проведите через прямую а плоскость, параллельную прямой Ь. 19. Проведите через данную точку отрезок так, чтобы его проекция на данную плоскость была равна длине отрезка. 20. В кубе ABCDAiBlC1Dl проведите сечение через: 1) ребра АВ и DiQ; 2) ребро AD и середину ребра ВВг; 3) середину ребер AD и DC параллельно ребру DDX; 4) середину ребра CCt параллельно ребрам АВ и A^D^. 21. В тетраэдре SABC проведите сечение через середину ребра АС параллельно ребрам АВ и CS. 22. С ребер BS и CS и внутреннюю точку D ребра АС. 23. Дан параллелепипед ABCDA^^C^D^. Постройте точку пересечения прямой ACt с плоскостью, проходящей через ребра DC и AtBv 5. Параллельные плоскости 24. Через точку грани ASB тетраэдра SABC проведите сечение, параллельное: 1) плоскости грани АВС; 2) плоскости грани ASB. 25. Через точку на боковой грани призмы проведите сечение, параллельное: 1) плоскости основания призмы; 2) плоскости данного диагонального сечения призмы. 26. Две прямые, проведенные из точки S, пересекают три параллельные плоскости соответственно в точках Аи А2, А3 и Ви В2, Въ. Известно, что AtA2 = 4 см, В2ВЪ = 9 см, A2A3 = BtB2. Вычислите AtA3 и BtB3. 27. В тетраэдре SABC проведены сечения А1В1С1 и А2В2С2, плоскости которых параллельны грани АВС. Известно, что SB1=A1A2 = 6 см, С1С2 = В2В= 12 см, SAi=4 см. Вычислите SA, SB, SC. §2. ПЕРПЕНДИКУЛЯРНОСТЬ В ПРОСТРАНСТВЕ.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |



 о
о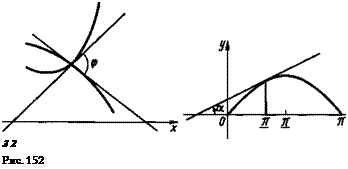
 Hi
Hi 5(4; 4). Записав уравнение параболы в виде 7 = (1/4)л:2, найдем к=у' = (\/2)х. Угловой коэффициент касательной в точке А есть А:(—2)=(1/2) *(—2)=-1; угловой коэффициент касательной в точке В равен к (4) = (1/2) *4=2.
5(4; 4). Записав уравнение параболы в виде 7 = (1/4)л:2, найдем к=у' = (\/2)х. Угловой коэффициент касательной в точке А есть А:(—2)=(1/2) *(—2)=-1; угловой коэффициент касательной в точке В равен к (4) = (1/2) *4=2.


 х
х
 В тетраэдре SABC провести сечение плоскостью, проходящей через три точки К,, L, М, лежащие соответственно на ребрах SA, SB и АС (прямые KL и АВ не параллельны; рис. 158).
В тетраэдре SABC провести сечение плоскостью, проходящей через три точки К,, L, М, лежащие соответственно на ребрах SA, SB и АС (прямые KL и АВ не параллельны; рис. 158). Через данную точку проведите прямую, скрещивающуюся с данной прямой.
Через данную точку проведите прямую, скрещивающуюся с данной прямой. Постройте сечение тетраэдра SABC плоскостью, проходящей через середину
Постройте сечение тетраэдра SABC плоскостью, проходящей через середину


