
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы умножения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: Р(АВ)=Р(А)Р(В). (16.18) Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле Р(А1А2...Ап)=Р(А1)Р{Аг)...Р(А,). (16.19) Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго: Р(АВ) = Р(А) • РА&) = Р(В) • РВ{А). (16.20) 43. В одной урне находятся 4 белых и 8 черных шаров, в другой—3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми. О Пусть А — появление белого шара из первой урны, а В—появление белого шара из второй урны. Очевидно, что события А и В независимы. Найдем />(Л)=4/12 = 1/3, Р(2?) = 3/12 = 1/4. По формуле (16.18) получим Р(АВ)=Р(А) Р(В) = (\!Ъ) (1/4)= 1/12 = 0,083. • 44. В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали. Найти вероятность того, что обе детали окажутся стандартными. О Введем следующие обозначения: А—первая взятая деталь стандартная; В—вторая взятая деталь стандартная. Вероятность того, что первая деталь стандартная, составляет Р(у4)=8/12 = 2/3. Вероятность того, что вторая взятая деталь окажется стандартной при условии, что была стандартной первая деталь, т. е. условная вероятность события В, равна РА(В)=1/\\. Вероятность того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий: Р(АВ)=Р(А) • Ра(В)=(2/3) • (7/11)= 14/33 = 0,424. * 45. Рабочий обслуживает два автомата, работающих независимо друг от друга. Вероятность того, что в течение часа первый автомат не потребует внимания рабочего, равна 0,8, а для второго автомата эта вероятность равна 0,7. Найдите вероятность того, что в течение часа ни один из автоматов не потребует внимания рабочего. 46. В урне находятся 6 шаров, из которых 3 белых. Наудачу вынуты один за другим два шара. Вычислите вероятность того, что оба шара окажутся белыми. 47. В урне находятся 10 белых и 6 черных шаров. Найдите вероятность того, что три наудачу вьшутых один за другим шара окажутся черными. § 5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА Пусть события (гипотезы) Blt В2, Вп образуют полную группу событий и при наступлении каждого из них, например Вь событие А может наступить с некоторой условной вероятностью Рв [А). Тогда вероятность наступления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А: Р(А)=Р{В,) ■ PBi (Л)+Р(В2) ■ РВг (А)+... + Р(ВЯ) ■ РВп (А), (16.21) где Р(2*1)+Р(52)+...+Р(Д,,)=1. Формула (16.21) называется формулой полной вероятности. Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) Blt В2,..., Вп, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса (формуле вероятности гипотез): , 4 PaW-Pb, Ра(В,)=-------- ■, (16.22) где РА(В,)—вероятность каждой из гипотез после испытания, в результате которого наступило событие А; Рв (А)—условная вероятность события А после наступления события Вь а1 Р(А) находится по формуле полной вероятности (16.21). 48. На склад поступили детали с трех станков. На первом станке изготовлено 40% деталей от их общего количества, на втором— 35% и на третьем 25%, причем на первом станке было изготовлено 90% деталей первого сорта, на втором—80% и на третьем — 70%. Какова вероятность того, что взятая наугад деталь окажется первого сорта? О Введем следующие обозначения: Вх—деталь изготовлена на первом станке, В2—на втором станке и Въ—на третьем станке; событие А—деталь оказалась первого сорта. Из условия следует, что Р(51)=0,4, Р(Я2)=0,35, Р(Я3) = 0,25, Рв (А)=0,9, Рв (у4)=0,8 и Рв (4)=0,7. Следовательно, Р{А) = Р{В,) • PBi(A) + P(B2) • РВг{А) + Р(Въ) • РВъ(А) = =0,4 • 0,9+0,35 • 0,8 + 0,25 *0,7=0,815. * 49. В первом ящике имеются 8 белых и 6 черных шаров, а во втором—10 белых и 4 черных. Наугад выбирают ящик и шар. Известно, что вынутый шар—черный. Найти вероятность того, что был выбран первый ящик. О Введем обозначения: В±—был выбран первый ящик; В2 — был выбран второй ящик; А—при проведении двух последовательных испытаний выбора ящика и выбора шара был вынут черный шар. Тогда Р(В1)=\/2, р(52)= 1/2. Вероятность извлечения черного шара после того, как выбран первый ящик, составляет Р „ (^4) = 6/14 = 3/7. Вероятность извлечения черного шара после того, как выбран второй ящик, равна РВ (А)—4/14=2/7. По формуле полной вероятности находим вероятность того, что вынутый шар оказался черным: Р(А) = Р(В\) РBl(A) + Р{В2)'?Bl(Л)=(1 /2)• (3/7)+(1 /2)• (2/7) = 5/14. Искомая вероятность того, что черный шар был вынут из первого ящика, вычисляется по формуле Байеса: Р (п\ РЫ РвМ (1/2)-(3/7) 3 Рл{В'}- Р(А) ~ 5Д4 _5-0’6' • 50. В урну, содержащую три шара, положили белый шар, после чего из нее наугад вынули один шар. Найдите вероятность того, что извлеченный шар окажется белым, если все возможные предположения о первоначальном составе шаров (по цвету) равновозможны. 51. В ящике сложены детали: 16 деталей с первого участка, 24—со второго и 20—с третьего. Вероятность того, что деталь, изготовленная на втором участке, отличного качества, равна 0,6, а для деталей, изготовленных на первом и третьем участках, вероятности равны 0,8. Найдите вероятность того, что наудачу извлеченная деталь окажется отличного качества. 52. На двух автоматах производятся одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата втрое больше производительности второго. Первый автомат в среднем производит 80% деталей первого сорта, а второй—90%. Взятая наудачу с конвейера деталь оказалась первого сорта. Найдите вероятность того, что эта деталь произведена первым автоматом. 53. Имеются три партии деталей по 30 шт. в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 30, 25 и 20. Из произвольно выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найдите вероятность того, что детали были извлечены из третьей партии. § 6. ПОВТОРЕНИЕ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛЛИ Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А. Вероятность того, что в п независимых испытаниях, в каждом из которых вероятность появления события А равна р (где 0</><1), событие А наступит ровно к раз (безразлично, в какой последовательности), находится по формуле Бернулли: Р"^к^кЦп-к)'.^= гДе Я=\~Р- (16.23) 54. Вероятность попадания в цель при одном выстреле составляет /?=0,8. Найти вероятность четырех попаданий при шести выстрелах. О Здесь w = 6, к=4, /> = 0,8, q=0,2. По формуле Бернулли находим Ре (4)=щ-щ • (0,8)4 • (0,2)4 • (0,2)6 -4=^ • (0,8)* • (0,2)2 = 0,246. • 55. Вероятность попадания в цель при одном выстреле составляет 0,8. Найдите вероятность трех попаданий при четырех выстрелах. 56. Всхожесть семян оценивается вероятностью 0,8. Какова вероятность того, что из пяти посеянных семян взойдет три? 57. При обработке деталей на станке в среднем 4% из них бывают с дефектами. Какова вероятность того, что каждые две детали из 30 взятых на проверку окажутся с дефектами? § 7. СМЕШАННЫЕ ЗАДАЧИ 55. Решите уравнения: (в+2)1 (fe+1)! } п\ Ш’ l) (fc—1)! ’ 2) 8Ся2^1 = 5С"2л++22; 4) 13С"2Г = 8C5„-+1i; Is'"’"' 5) Ci.-Ci, 59. Решите неравенства: 1) ^—^<20; 2) ~—^г>30. ^ 7 (л—3)! 7 (и-3)! 60. Число сочетаний из п элементов по 4 относится к числу сочетаний из п + 2 элементов по 5, как 5:18. Найдите п. 61. В ящике находятся 6 белых и 10 черных шаров. Наудачу вынимают одновременно два шара. Найдите вероятность того, что оба шара окажутся черными. 62. В урне находятся 6 белых и 4 черных шара. Вынимают один за другим два шара. Найдите вероятность того, что оба шара окажутся черными. 63. В урне находятся 15 белых и 6 черных шаров. Из нее вынимают наугад один шар, снова возвращают его в урну и шары перемешивают. Затем вынимают второй шар. Найдите вероятность, что оба вынутых шара белые. 64. В первой урне находятся 10 белых и 2 черных шара, а во второй—4 белых и 8 черных шаров. Из каждой урны вынули по шару. Какова вероятность того, что оба шара окажутся черными? 65. На отдельных карточках написаны буквы «и», «л», «о», «е», «ч». После перемешивания берут по одной карточке и кладут последовательно рядом. Вычислите вероятность того, что из этих букв составится слово «число». 66. Три стрелка стреляют по мишени. Вероятности попадания в цель для первого, второго и третьего стрелков соответственно равны 3/4, 4/5 и 9/10. Найдите вероятность того, что все три стрелка одновременно попадут в цель. 67. На книжной полке произвольным образом расставлены восемь книг. Вычислите вероятность того, что три определенные книги окажутся поставленными рядом. 68. На трех автоматических линиях изготовляются одинаковые детали. На первой линии изготовляется 50% всех деталей, на второй—30% и на третьей—20%. При этом на первой линии изготовляется 0,025 нестандартных деталей, на второй—0,02 и на третьей—0,015. Найдите вероятность того, что наудачу взятая из готовой продукции деталь окажется стандартной. 69. Монету подбрасывают 10 раз. Какова вероятность т^го, что при этом «герб» выпадет 3 раза? 70. В ящике находятся 60 стандартных и 40 нестандартных деталей. Найдите вероятность того, что из взятых наудачу двух деталей одна окажется стандартной, а другая нестандартной. ЗАЧЕТНАЯ РАБОТА
I вариант 1) Докажите тождество Си9 + Си8 = Си9+1. 2) Решите уравнение п\ 20 п\ II вариант 1) Докажите тождество з + CJh- з = С^+4. 2) Решите уравнение (2л)! 40л!
(п_5)! („-3)' 3) Решите уравнение scs^ecs.-!. 4) Талоны, свернутые в трубочку, занумерованы всеми двузначными числами. Наудачу берут один талон. Какова вероятность того, что номер взятого талона состоит из одинаковых цифр? 5) В ящике находятся детали, из которых 12 изготовлены на первом станке, 20 — на втором и 16—на третьем. Вероятность того, что детали, изготовленные на первом, втором и третьем станках, отличного качества, соответственно равна 0,9; 8 и 0,6. Найдите вероятность того, что извлеченная наудачу деталь окажется отличного качества. (2л—3)! (и— 1)!' 3) Решите уравнение nr^n-l __ О/^И— 1 2п-2 — Э1~ 2и-1- 4) В урне 12 шаров. Среди этих шаров 3 белых и 9 черных. Какова вероятность того, что наудачу вынутый шар окажется белым? 5) На двух поточных линиях производятся одинаковые изделия, которые поступают в ОТК. Производительность первой поточной линии вдвое больше производительности второй. Первая поточная линия в среднем производит 70% изделий первого сорта, а вторая— 90%. Наудачу взятое ОТК на проверку изделие оказалось первого сорта. Найдите вероятность того, что это изделие произведено на первой поточной линии. РАЗДЕЛ Ш ГЕОМЕТРИЯ Глава 17 ВЕКТОРЫ НА ПЛОСКОСТИ § 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 1. Параллельный перенос. Преобразование фигуры F на плоскости, при котором ее произвольная точка с координатами (х, у) переходит в точку с координатами (ха; у+b), где а и Ъ—постоянные, называется параллельным переносом. Параллельный перенос задается формулами х'=х+а, у'=у + Ь, (17.1) где (х'; У)—координаты точки, в которую переходит точка (jc; у) при параллельном переносе. 2. Понятие вектора. Отрезок называется направленным, если один из его концов считается началом отрезка, а другой—его концом. Вектором называется направленный отрезок. Вектор, заданный парой (А, В) несовпадающих точек, обозначается символом АВ. Точка А называется началом,[, а точка В—концом вектора. ) Расстояние \АВ\ называется длиной (модулем) вектора АВ. Для обозначения векторов употребляются также строчные латинские буквы со стрелкой наверху: а, В,..., х, у. Вектор А А, концы которого совпадают, называется нулевым вектором. Длина нулевого вектора равна нулю. Понятие направления для нулевого вектора не вводится. ж Каждый вектор, отличный от нулевого, вполне характеризуется своим направлением и длиной. 3. Коллинеарные векторы. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору. Если два ненулевых вектора а и В коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы а и В называются сонаправленными (а\\В), во втором—противоположно направленными (а\ [В). 4. Равенство векторов. Два вектора называются равными, если они совмещаются параллельным переносом, т. е. если существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Другими словами, равные векторы сонаправлены и равны по модулю, т. е. если а=В, то a]]b и \а\ = \В\, и, обратно, если векторы сонаправлены и равны по модулю, то они равны, т. е. если а]]В и \а | = |£|, то а—В. Любой^ вектор j)aeeH самому себе: а=а. Если а —В и Ь=с, то а=с. 5. Откладывание вектора от данной точки. Из любой точки плоскости можно отложить единственный вектор, равный данному вектору. Построение вектора MN, равного вектору а, называют откладыванием вектора а от точки М (рис. 96). Чтобы построить вектор MN=a, проведем из точки М луч, сонаправ- ленный с_вектором а, и отложим на нем отрезок MN такой, что MN=\a |. Тогда MN=a. 1. Параллельный перенос переводит точку (2; 3) в точку (—3; 2). В какую точку он переведет точку (5; —2)? О Используя формулы (17.1), находим значения а и Ь, соответствующие параллельному переносу точки (2; 3) в точку (—3; 2): -3 = 2+я, 2=3 + Ь, т. е. а=-5, 6= — 1. Далее, по формулам (17.1) получаем *' = 5 — 5 = 0, /= —2 —1 = —3, т. е. точка (5; —2) переходит в точку (0; —3) (рис. 97). ф 2. Параллельный перенос переводит точку (—4; 1) в точку (2; —3). В какую точку он переведет точку (5; 5)? 3. Параллельный перенос переводит начало координат в точку (—3; — 5). В какую фигуру он переведет треугольник ЛВС с вершинами А(—2; 6), В (4; 8), С (5; 3)? 4. Дан параллелограмм. Выполните параллельный перенос, который отображает точку пересечения его диагоналей в одну из его вершин. 5. Сколько векторов задают всевозможные упорядоченные пары точек, составленные из вершин: 1) треугольника; 2) параллелограмма? 6. Даны пары точек: 1) (-2; -3); (5; 4); 2) (6; -2), (13; 5); 3) (—8; —5), (—1; 1). Укажите, какие пары определяют равные векторы. 7. Дан параллелограмм ABCD; О—точка пересечения его диагоналей. Какие пары, составленные из точек А, В, С, D и О, определяют один и тот же вектор? § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО 1. Сложение векторов. Для того чтобы построить сумму двух данных векторов а и В, нужно выбрать произвольную точку А и отложить от нее вектор АВ=а, а затем от точки В отложить вектор ВС=Б. Тогда вектор АС является искомой суммой: а+В=АВ +ВС=АС=а (рис. 98). Вектор с=а+В называют замыкающим вектором, а векторы а и В — составляющими векторами. Этот способ построения называется правилом треугольника.
Правило треугольника можно сформулировать_и так: если А, В и С—произвольные тонки плоскости, то АВ+ВС=АС. Это равенство называют правилом трех точек. Сумму двух данных векторов а и В можно построить и следующим образом. Откладывая от произвольной точки О (рис. 99)_векторы ОА=а и ОВ=В, построим параллелограмм О АС В. Тогда вектор ОС (где [OCJ—диагональ параллелограмма) является искомой суммой: а+В=ОА +ОВ= = ОА + АС=ОС=с7 Этот способ построения называется правилом параллелограмма. Для того чтобы построить сумму п данных векторов а19 а2, •••, аю нужно от произвольной точки О отложить вектор al9 затем от конца вектора я j отложить вектор а2, наконец, от конца вектора отложить вектор ап. Тогда вектор, начало которого совпадает с началом вектора а 1?ji конец—с концом вектора ап, является искомой суммой: с=а 1+а2 + \... + ап (рис. 100). 2. Вычитание векторов. Два вектора называются противоположными, если их сумма равна нулевому вектору. Вектор, противоположный вектору а, обозначают—а. Таким образом, а+(—а)=0. Ненулевые противоположные векторы имеют равные длины и противоположные направления (рис. 101). Вектор с называется разностью вео'оров а и Ь, если с+Ь = а. Чтобы вычесть из вектора а вектор достаточно прибавить к вектору а вектор, противоположный вектору 5, т. е. а—В=а+(—В) ^ (рис. 102). Другой способ построения разности векторов а и В состоит в следующем. Откладывая от произвольной точки О векторы ОА=а и ОС——В (вектор, противоположный вектору В), получим ОВ=а—В (рис. 103). 3. Умножение вектора на число. Произведением ненулевого вектора а на число т называется вектор, имеющий направление вектора а, если га>0, и противоположное направление, если т< 0. Длина этого вектора равна произведению длины вектора а на модуль числа т.^ Произведение вектора а на число т обозначается та. При любых ти а векторы та и а коллинеарны и \та \ = \т\ -\а |.
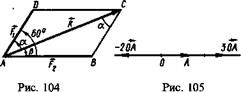
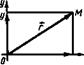
4. (а, Ъ)=ф, где (Кф<180°. ^ ^ Частные случаи: 1) если а\]В, то (я, Ь)=0; 2) если а][В, то (а,Л5') = 180°. _ _ 8. Дано: а, В, (а, Ь). Найти модуль вектора с = а + 5. О По теореме косинусов имеем c2 = a2+b2 — 2abcosC. Так как cos С=cos [180°—(а, В)] = —cos(а, В), то * с = \/a2-\-b2 + 2 ab cos (af^B ). • 9. Найти модуль равнодействующей R двух сил и F 2 и углы, образуемые равнодействующей с силами и f2, если Ft=4H и jp2 = 6 Н, а ф = 60° (рис. 104). О Используя формулу предыдущей задачи, находим JR=v/42 + 62 + 2-4-6 cos60° =,/16+ 36+ 24=^/76 = 8,72 (Н). По теореме синусов имеем F2/smoL=Fl/sin (3 = Л/sin(180° — ф)=Д/sin ф. Следовательно, sin а=(F2 sin ф) / R=(6 sin 60°)/ 8,72 = 0,596; а=36°, 6; sin р=sin ф)/JR=(4 sin 60°)/8,72 = 0,397; p = 23°, 4. Контрольное вычисление: а+р = 36°,6+23°4, = 60°. ф Ю^Цан ненулевой вектор^ О А. Отложить от точки О векторы: 1) ЗОЛ; 2) -20А; 3) 0,504; 4) -0,7504; 5^^204. О На рис. 105 изображены векторы ЗОЛ и —20А. Остальные векторы отложите самостоятельно, ф 11. Векторы АС=т и BD=n сл^жат^диагоналями параллелограмма ABCD. Выразить векторы АВ, ВС, CD и DA через тип (рис. 106). О По определению суммы и разности векторов_^имеем BC+CD=n, BC—CD=m. Сложив эти равенства, получим ВС=(т+п)/2. Далее, находим:, CD=n—BC = и — ( т+п)/2 = (п—т)/2, АВ= —(п—т)/2=(т—п)/2, DA = —ВС= —(т+п) /2. ф 12. По данным векторам а, В, с постройте вектор а+В + с. 13. Какому условию должны удовлетворять три вектора а, В и с, чтобы из них можно было образовать треугольник? 14. Найдите модуль равнодействующей двух^ил Ftи F 2и углы, образуемые равнодействующей с силами Fxи F ъ если модули сил равны Fx = 8Н и /Г2 = 5Н, а угол между ними равен 30°. 15. При каких значениях m длина вектора jna (где аф]0) удовлетворяет условиям: 1) \та\ = \а\; 2) \та\>\а\; 3) |wa|<|a|? 16. В треугольнике ЛВС медианы ААХ и СС1 пересекаются в точке М. Найдите множитель т, если: 1) АХС =т-ВС\ 2) С^В =т-С1А; 3) АМ = т-МА~\ 17. Точка М—середина стороны треугольника АВС. Выразите СМ через векторы АВ и ВС. 18. Докажите, что средняя линия трапеции равна полусумме ее оснований. 19. Дан правильный шестиугольник ABCDEF, О—его центр, ОА = а, О В = В.Найдите ОС, OD, ОЕ и OF. § 3. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ 1. Ось. Угол между вектором и осью. Прямая, на которой выбрано положительное направление и задана единица измерения длины, называется осью. Вектор е, имеющий длину | е \ = 1 и направление, совпадающее с направлением оси, называется единичным вектором (ортом) этой оси. Если аф0 и е—вектор единичной длишл, направление которого Совпадает с направлением вектора а\ jo а=\а\-е. Углом между ненулевым вектором аФ 0 и осью I называется угол между направлениями оси и вектора: (а, /) = ф, где 0^ср<180°. 2. Проекция вектора на ось. Проекцией вектора на ось называется направленный отрезок на оси, начало которого есть проекция начала вектора и конец — проекция его конца. Длина этого направленного отрезка берется со знаком плюс, если направления отрезка и оси совпадают, и со знаком минус, если их направления противоположны (рис. 107). Проекция вектора а^О на ось / равна длине этого вектора, умноженной на косинус угла <р между осью и вектором (рис. 108): npta = \ а | coscp. (17.2) Отметим свойства проекций: пр/(л+5) = пр,я + пр,5; пр 1(та) = т прta. 3. I Рис. 109 прямоугольным базисом на плоскости. Совокупность начала О и прямоугольного базиса (/, j) называют прямоугольной системой координат^ на плоскости. Точку О называют началом координат, а векторы Г и j — координатными векторами. 4. Координаты вектора. Вектор, направленный из начала координат в произвольную точку М плоскости хОу, называется радиусом-вектором точки М и обозначается г: ОМ = г (рис. 110). Проекции вектора г на координатные оси, т. е. прхг=л; и прУг=у, называются координатами ^вектора (рис. 110). Координаты вектора г кратко записывают так: г=(х; у).
Рис. 112
Координаты радиуса-вектора г=ОМ являются одновременно координатами точки М, т. е. конца радиуса-вектора г. Если начало вектора а = АВ не совпадает с началом координат, то координаты вектора а и координаты его конца различны (рис. 111). В этом случае проекции вектора а = АВ на оси координат соответственно равны х=хв-хА и у=ув-уА, Т._е. а=АВ ={х; у)=(хв-хЛ; ув-ул). (17.3) 5. Разложение вектора по координатным осям. Разложение вектора а в базисе (/, ]) имеет вид a=xT+yj, (17.4) где /—единичный вектор на оси Ох, а /—единичный вектор на оси Оу (рис. 112). Числа х и называются координатами вектора а в базисе (£ /). Векторы xi и yj называются составляющими (или компонентами) вектора а по осям координат. Если начало вектора а находится в точке А(ха; уА), а конец—в точке В(хв; ув), то разложение вектора а записывается в виде а=АВ =(хв-хА)1+(у B-yA)j. (17.5) 6. Правила действий над векторами, заданными своими координатами. Если в базисе (?,у) заданы векторы а = (х1\у^) и В=(х2;у2)> то: координаты суммы двух (или более) векторов равны суммам соответствующих координат слагаемых, т. е. a+b = (x j +jc2; ух +у2); координаты разности двух векторов равны разностям соответствующих координат этих векторов, т. е. a—b = (xl — x2;yl—y2); координаты произведения вектора на число равны произведениям соответствующих координат данного вектора на это число, т. е. та = (тх myj. 7. Условие коллинеарности двух векторов. Условие коллинеарности двух векторов а = (х1;у1) и Ь = (х2;у2) имеет вид xl=mx2, 7i — ту2, (17.6) т. е. если соответствующие координаты двух векторов пропорциональны, то векторы коллинеарны. т-2)
Если т>О, то векторы а и Ь имеют одинаковое направление; если т<О, то направления векторов противоположны. 20д Дано пр*я=—2; uptB=\. Вычислить: 1) пр*(2а+5); 2) пр,(Зо—25). О Используя свойства проекций, получим: 1) пр,(2я+Й) = 2пр z я+пр, 5=2 * (—2)-h 1 = —3; 2) npl(3e-25) = 3npIe-2nplf=3 (—2)—2• 1 = —8. * 21. Найти проекцию вектора а на ось /, образующую с вектором угол 60°, если \а\ = 6. О По формуле (17.2) получим пр,я = 6 cos60° = 3. ф 22. Построить: 1) вектор а = (3; —2); 2) вектор а = АВ, если Л(-1; -2), 5(4; 3). О 1) Строим радиус-вектор с концом в точке ЛГ(3; —2) (рис. 113). Радиус-вектор ОМ—искомый. 2) Строим точки А(— 1; —2)—начало вектора и 2?(4; 3)—конец вектора (рис. 114). Вектор АВ—искомый, ф 23. Найти координаты вектора а = АВ, если А(— 1; —2), /?(4; 5). О По формуле (17.3) получим а=АВ=(4—(—1); 5—(—2))=(5; 7). • 24. Выразить через единичные векторы iи jследующие векторы: о=(—2; 4); 2) а=ЛЯ, А{-2; -1), 5(4; -3). О 1) Здесь х= —2, у=4. По формуле (17.4) получим а= — 2Н-4/ 2) По формуле (17.5) находим а=АВ=(4—(—2))Т+(—3—(— 1))/=бГ—2/ • 25. Проверить, коллинеарны ли векторы АВ и С/); если да, то сонаправлены ли они. Векторы соответственно заданы точками: A(l; 1), 5(7; 3), С(-4; -5) и £>(5; -2); 2) ^(2; 1), В(-4; 4), С(—1; -1) и £)(7; -5); 3) Л(2; 1), 5(6; 5), С(3; -1) и D(7; -2). О 1) По формуле (17.3) находим координаты векторов: АВ=(6; 2), С/)=(9; 3). Используя соотношения (17.6), устанавливаем, что координаты этих векторов пропорциональны: 6/9 = 2/3=т>0; следовательно, векторы коллинеарны и сонаправлены. 1) Аналогично получаем: АВ=(— 6; 3), CZ>=(8; —4), (—6)/8 = 3/(—4)= =т< 0; следовательно, векторы коллинеарны и противоположно направлены. 2) Имеем АВ=(4; 4), С£>=(4; —1); так как 4/4^(—1)/4, то координаты не пропорциональны и, следовательно, векторы не коллинеарны. ф 26. Дано: npta= — 1, ^,5 = 3. Вычислите: 1) прДя—В); 2) пр,^а+£^. 27. Докажите, что если для двух непараллельных осей / и п выполнены соотношения пр,я = 0 и пр„а = 0, то а = 0. 28. В каком случае проекция вектора на ось: 1) равна нулю; 2) равна по абсолютной величине длине данного вектора? 29. Векторы а и В симметричны относительно прямой /. Каким соотношением связаны между собой проекции этих векторов на ось п: 1) параллельную прямой /; 2) перпендикулярную прямой /? 30. Даны векторы а и В. _При каком положении оси / справедливо равенство пр/а = пр/5? 31. Найдите проекцию вектора а на ось /, образующую с вектором угол: 1) 45°; 2) 120°; 3) 150°. ^ 32. Постройте векторы: 1) а = (—2; 4); 2) В=(3; 2); 3) а=АВ, если А(-1; -1), В(4; 1); 4) c = CZ), если С(0; 2), D(4;6\. 33. Найдите координаты вектора: 1) а=АВ, А (— 2; —2), В(4; -1); 2) £=ЯС, JB(l; -3), С(4; г5). 34. Даны векторы а ==[ — 2; — 3], £=(5; J)), с=(3; — 5). Найдите коо]эдиваты ректоров: 1) а+В; 2) а—с; 3) а+В— с; 4) 2а; 5) За — с; а—2Ь + 2с. 35. Выразите через единичные векторы Г и / векторы: а —(—2; -4); 2) а=АВ; А(-1; 2), 2?(-2; -6). 36. Даны точки: Л(—2; —3), В(2; 4) и С(5; 1). Разложите векторы А В, ВС и С А по единичным векторам i n_J. 37. Проверьте, коллинеарны ли векторы АВ и CD; если да, то сонаправлены ли они. Векторы соответственно заданы точками: А{-3; 6), В(1; 2), С(4;-6) и £>(-2; 0); 2) Л(-3; 1), 5(3; 3), С(-2; -3) и Z>(6; -1); 3) А(-3; -6), В{-1; 2), С(3; -5) и /)(5; 3). § 4. ДЛИНА ВЕКТОРА. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ НА ПЛОСКОСТИ. УГЛЫ, ОБРАЗУЕМЫЕ ВЕКТОРОМ С ОСЯМИ КООРДИНАТ Длина радиуса-вектора а=(х; у) находится по формуле \а\=1/х2+у2. (17.7) Длина вектора а=АВ=(хв—хл; Ув~Уа) находится по формуле \Гв\=^{хв-х]1+(ув-ул)1. (17.8) С помощью этой формулы вычисляется также расстояние между двумя точками на плоскости. ^ Углы, образуемые вектором а = АВ с осями координат Ох и Оу, находятся по формулам cos ci=—— Хв Хл cos ft=—- - - Ув Ул (17.9) у/(хв-х а)2 + (Ув-Уа )2 У(^в -^)2 + (Уя -^)2 38, Найти длину вектора АВ, если А(1; 1) и В(4; — 3). Q По формуле (17.8) находим |AB\-yJ(A—1)2+(— 3—1)2 = 5. ф Л - 39. Найти единичный вектор того же направления, что и вектор: а — (3; 4); 2) Ь = (-6; -8). О 1) Находим длину данного вектора: | а | = ч/32+42 = 5. Единичный вектор е того же направления, что и вектор а, равен е—а /\а \ = (\/5)а. Каждая проекция вектора е также в пять раз меньше соответствующей проекции вектора а, поэтому е=(3/5) Г+ (4/5)I или?=(3/5; 4/5). 2) Аналогично получим е = (—0,6; —0,8). # 40. Найти косинусы углов, образуемых заданными векторами с осями координат: 1) а — АВ, А(2; —3); 5(1; 4); 2) Ь = ВС, 5(— 1; 1), С(2; 5). 1) По формулам (17.9) находим 1-2 г cos а = —- — —= —0,1 х/2; v/(1_2)2 + (4+3)2 4+3 г cos Р= - - =0,7Л/2. л^/ (1 — 2) +(4+3)2 2) В этом случае получаем cos а = 0,6; cos р = 0,8. ф 41. Даны тючки А[4; 0), 5(7; 4) и С (— 4; 6). Найдите длины векторов: 1) АВ; 2) 2?С; 3) С4. 42. Вычислите периметр треугольника, вершинами которого служат точки: 1) А (4; 0), В(1\ 4) и С(-4; 6); 2) Л (6; 7), В(3; 3) и С(1; -5). 43. Найдите косинусы углов, образуемых заданными векторами с осями координат: 1) а = АВ, А(—2; —3); 5(3; 9); 2) 8= ВС, 5(4; -1); С(0; 2). 44. Найдите точку, равноудаленную от точек: 1) А(1; —1), 5(—2; 2) и С(— 1; -5); 2) ^(10; 7), 5(-4; -7) и С(12; -7). 45. Найдите центр окружности, проходящей через точки А(— 1; 9), 5(—8; 2), С(9; 9), и длину ее радиуса. 46. Расстояние от точки М, лежащей на оси Ох, до точки Дг(10; 5) равно 13. Найдите точку М. 47. Расстояние от точки 5, лежащей на оси Оу, до точки А(3; —1) равно 5. Найдите точку 5. 48. Вычислите координаты точки на оси Оу, равноудаленной от точек: 1) А(— 4; 0) и 5(— 3; —7); 2) Л(— 3; —1) и 5(6; 2). 49. Найдите точку на оси Ох, равноудаленную от точек: А(5; 13) и 5(—12; -4); 2) А(0; 6) и 5(2; -4). 50. Вычислите координаты точки М, равноудаленной от осей координат и от точки: 1) А(— 8; —1); 2) А (4; 2). 51. Найдите точку М, расстояние которой от оси ординат и от точки А (8; 6) равно 5. 52. Вычислите координаты точки М, расстояние которой от оси абсцисс и от точки А(1; 2) равно 10. Если отрезок АВ разделен точкой С в отношении АС:СВ=Х, то координаты точки С находятся по формулам u * Хл + Ъь _Ул+Ъв я. п- Хс" \+Х ' Ус~ 1+Х • п (17Л°) Если X = 1, то получаются формулы для нахождения координат середины отрезка: *А+хв Уа+Ув ,^11Ч *с=—^—’ Ус= 2 ‘ ** 53. Отрезок, концы которого А (—11; 1) и В(9; И), разделен в отношении 2:3:5 (от А к В). Найти точки деления. О Обозначим точки деления от А к В через С и D. По условию, хА= — 11, хв = 9, уА= 1, ув= 1 и AC:CD:DB=2:3:5. Точка С делит АВ в АС 2 2 1 отношении л,=------- =------ =-=-• значит, СВ 3+5 8 4 _ 11Ч- (1 /4) • 9________ _ 1 +(1/4) 11 1 + 1/4 - 7’, + 1/4 -3, С(7,3). Точка D служит серединой А В, поэтому “п+9,! + п ^ *d=—=—=-i; Уо=—^—=^ />(—1; 6). • 54. Даны вершины треугольника А(хл; уА), В(хв; ув) и С(хс; ус). Найти точку пересечения медиан этого треугольника. О Известно, что медианы треугольника пересекаются в одной точке, которая делит каждую из медиан в отношении 2:1, считая от соответствующей вершины треугольника. Найдем точку D—середину стороны ВС: xD=(xB+xc)/2, yD = (yB+yc)/2- Находим точку М, в которой пересекаются медианы; для этого разделим медиану AD в отношении Х = 2:1=2 (от А к D): _xA + XxD _ха + 2-(хв+хс)/2 _хА+хв+хс Хм 1+Х Г+2 ~ 3 ’ _Ул+ЬУр _Ул+2- {Ув+Ус)/2 У л +Ув+Ус Ум 1+Х 1+2 3 Таким образом, координаты точки пересечения медиан треугольника.равны среднему арифметическому одноименных координат его вершин, ф 55. Отрезок АВ задан точками А(— 9; —3) и 5(1; 2). До какой точки С нужно продолжить отрезок АВ, чтобы АВ:ВС =5:3? О По условию, хА—— 9, хв= 1, уА—— 3, ув = 2, Х=АВ:ВС= 5:3. Требуется найти С (хс/ ус). Для точки 5(1; 2), делящей отрезок АС в данном отношении, получим: -9+(S/3)*c -3+(5/3)yc + 5/3 ’ 1 + 5/3 ’ откуда xc = l, yc=5, т. e. С(7; 5). • 56. Вычислите координаты точки С—середины отрезка АВ, если: А(5; -4) и В(-1; 2); 2) Л(6; -3) и Я(-2; -7). 57. Точка С делит отрезок АВ в отношении 3:5 (от А к В). Концами отрезка служат точки А (2; 3) и В (10; 11). Найдите точку С. 58. Отрезок, концами которого служат точки А(3; —2) и 2?(10; —9), делится точкой С в отношении 2:5. Найдите точку С. 59. Отрезок, концами которого служат точки А(— 5; —2) и В(4; 2,5), разделен в отношении 3:4:2 от А к В. Найдите точки деления. 60. Концом отрезка служит точка v4(— 3; —5), а его серединой— точка С(3; —2). Найдите второй конец отрезка—точку В. 61. Найдите точку пересечения медиан треугольника, если вершинами его служат точки: 1) А(7; —4), В(— 1; 8) и С(—12; —1); 2) А(-4; 2), В(2; 6) и С(0; -2). 62. Концами отрезка служат точки А(—8; — 5) и 5(10; 4). Найдите точки Си D, делящие этот отрезок на три равные части. 63. Точка С(3; 5) делит отрезок АВ в отношении АС:СВ=ЪА. Найдите начало отрезка—точку А, если его концом служит точка В(-1;1). 64. Точка С(— 2; 1) делит отрезок АВ в отношении АС:СВ=2:1. Найдите конец отрезка—точку В, если его началом служит точка А(—10; 5). 65. Отрезок задан точками А(—4; 7) и В(— 3; 5). Найдите на продолжении отрезка АВ такую точку С, чтобы АВ:ВС=\:7. 66. Отрезок задан точками А(—5; —2) и В(— 1; 0). До какой точки С нужно его продолжить, чтобы АВ:ВС=2:5? § 6. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение векторов а к Б обозначается символом а •b. Таким образом, по определению, a -Б=\ а | *|£| *cos(a,^5). (17.12) Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого вектора по направлению первого: а^=\а\п^Б=\Ь1пща. (17.13) Скалярным квадратом вектора а называется скалярное произведение а • а. Скалярный квадрат вектора равен квадрату его длины: а'а = а2. (17.14) Необходимым и достаточным условием перпендикулярности двух ненулевых векторов а и b является равенство нулю их скалярного произведения: (аф О, ЬФО, a-S=0)oa±S. (17.15) Необходимое и достаточное условие коллинеарности двух векторов а и Б состоит в выполнении соотношения аБ=±| а\\Б\ (17.16) (при этом знак плюс соответствует случаю а\\Б, а знак минус—случаю «!Й- Скалярное произведение векторов л=(^1;.у1) и b (х2; у2) выражается через их координаты по формуле а -Б=х1х2+у1у2. ' (17.17) Угол между двумя векторами а=(х1;у1) и Б(х2;у2) находится по формуле
|

 Рис. 98 Рис. 99 Рис. 100
Рис. 98 Рис. 99 Рис. 100
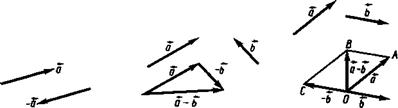
 Угол между двумя векторами. Углом между двумя ненулевыми векторами а и В называется угол между направлениями этих векторов:
Угол между двумя векторами. Углом между двумя ненулевыми векторами а и В называется угол между направлениями этих векторов: Прямоугольная система координат. Пусть на плоскости задана пара единичных взаимно перпендикулярных векторов i и у, отложенных от некоторого начала—точки О (рис. 109). Такую пару векторов называют
Прямоугольная система координат. Пусть на плоскости задана пара единичных взаимно перпендикулярных векторов i и у, отложенных от некоторого начала—точки О (рис. 109). Такую пару векторов называют


 to
to Рис. ИЗ
Рис. ИЗ


