Вычисление моментов инерции плоской фигуры

Моментом инерции материальной точки относительно оси называется произведение массы точки на квадрат ее расстояния до этой оси.

Моменты инерции материальной плоской фигуры D, распределение массы которой характеризуется плотностью 5=5 (х, у), вычисляются по формулам:

I_x=tty²b(x,y)dxdy

D

(момент инерции относительно оси Ох);

D

(момент инерции относительно оси Оу);

 

1о=$И^х2+У²)Ь(х, у) dx dy

D

(момент инерции относительно начала координат).

Величина /₀ называется полярным моментом инерции и может быть выражена равенством

Л) = ^х + /_Г

Если плоская фигура D является однородной и симметричной относи­тельно оси абсцисс (ординат), то момент инерции 1_Х(1_У) равен удвоенному моменту инерции относительно оси Ох (оси Оу) половины этой фигуры, расположенной по одну сторону от оси абсцисс (ординат).

71. Найти моменты инерции 1_Х, 1_У и /₀ пластинки, ограниченной параболой у=х² и прямой у = х, если плотность в каждой точке пластинки численно равна ординате этой точки.

О Парабола и прямая пересекаются в точке М (1; 1); значит, область D определяется системой неравенств O^x^l, х²^у^х. Используя формулы

(29.26), (29.27) и (29.29), получим

1 X

	Ix=^y^2ydxdy=^dx^y^3dy=^\y*Yxldx=^X-^{x*-x^s)dx=^(pn*y,
		D 0 jc* о О
		(ед^4). •

 

 

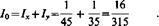
72. Найти момент инерции однородного квадрата со стороной, равной 3, относительно одной из его вершин.

О Совместим одну из вершин квадрата с началом координат, а координатные оси Ох и Оу направим по двум его сторонам, исходящим из этой вершины. Область D определяется системой неравенств 0^x0, О^у^З.

Искомый момент инерции найдем по формуле (29.28) при 6=1:

 

= 54 (ед.⁴) ф

73. Вычислите моменты инерции /_х, 1_У и /₀ однородной пластинки (8=1), ограниченной заданными линиями: 1) х—2, у=3, х=0, у=0; 2) у = х₉ х=4, у=0; 3) у=х², у= 1, х=0; 4) у = cosx, О^х^п/2.

74. Вычислите моменты инерции 1_Х9 1_У и /₀ пластинки, ограничен­ной параболой у=х²/4, осью Ох и прямой х=2, если плотность в каждой точке пластинки численно равна ординате этой точки.

75. Вычислите моменты инерции 1_Х, 1_у и /₀ квадратной пластин­ки, ограниченной осями координат и прямыми л;=1 и у= 1, если плотность в каждой точке пластинки численно равна квадрату расстояния от начала координат до этой точки.

76. Вычислите моменты инерции /*, 1_у и /₀ пластинки, ограничен­ной параболой у=х²/2, осью Оу и прямой х=2, если плотность в каждой точке пластинки численно равна абсциссе этой точки.

ЗАЧЕТНАЯ РАБОТА

 

I вариант

1) Найдите массу прямоугольной пластинки со сторонами 4 и 5, в каждой точке которой поверхност­ная плотность пропорциональна квадрату расстояния от одной из вершин прямоугольника до этой точки. Коэффициент пропорциональ­ности равен к.

2) Найдите статические моменты относительно осей Ох и Оу однород­ной пластинки (8=1), имеющей фор­му треугольника с вершинами О (0; 0); А (4; 4) и В (0; 6).

3) Найдите координаты центра тяжести пластинки, ограниченной параболой у=х² и прямой у= 1, если плотность в каждой точке пластин­ки численно равна ординате этой точки.

4) Найдите моменты инерции 1_Х, 1_У и /₀ однородной пластинки (8=1), ограниченной осями координат и прямыми х=6, у—4.

II вариант

1) Найдите массу прямоугольной пластинки со сторонами 3 и 4, в каждой точке которой поверхност­ная плотность пропорциональна сумме абсциссы и ординаты любой точки прямоугольника. Коэффициент пропорциональности равен к.

2) Найдите статические моменты относительно координатных осей пластинки, ограниченной параболой у²=х (у^0), прямой х=9, если плотность распределения массы в каждой точке равна ординате этой точки.

3) Найдите координаты центра тяжести пластинки, ограниченной параболой у=х²/2 и прямой у = 2, если плотность распределения массы в каждой точке пластинки численно равна ординате этой точки.

4) Найдите моменты инерции 1_Х,

1_У и /₀ однородной пластинки (5=1), ограниченной осями координат и прямой у —2 — 0,5л:.

ОТВЕТЫ

Глава 1

3. 1) 0,2; 2) 0,4; 3) 0,3; 4) 0,42. 4. 385,5<х<386,5. 5. 0,5. 6. 10,61 < 10,63< <10,65 (А). 7. 1,0077 <1,0082 <1,0087; 63,29 <63,44 < 63,59. 8. 24,2 < 24,5 < <24,8 (см²). 13. 1) 2; 2) 4,6 и 3; 3) 7; 4) 1, 2, 7 и 8; 5) 3. 14. Все три цифры верные. 15. Все цифры верны в строгом смысле. 16. 1) 28 • 10¹ ± 10; 2) 89 • 10²± ±100; 3) 53• 10⁴± 100; 4) 57,4 10²±10. 17. 1) 0,3+0,08; 2) 2,06±0,007; 3) 14± ±1; 4) 24,7± 0,1. 18. 1) 1,24-10⁴ ±50; 2) 1,58 • 10⁴± 100; 3) 8,7-10^[39]±50; 4) 8,1 х х 10²±10. 19. 1) До=0,01; 2) До=0,1; 3) До=0,01; 4) До=0,001. 20. 1) 0,01 10²;

2) 0,0001 10²; 3) 0,001 -ИГ⁴; 4) 0,01 Ю"³. 25. 0,05%. 26. 1) 2,1%; 1,4%;

2) 1,8%; 0,44%; 3) 1,3%; 0,14%. 27. 0,3%. 28. 2%. 29. 1, 2 и 8.

Глава 2

2. 24,5. 3. а=5,55; До=0,001; £„=0,00018. 4. о=6,61; До=0,0015; £„= =0,00023. 5. R= 18,8 Ом; ДА=0,06; e_R=0,3%. 7. 6,07. 8. а =1,37; До=0,001; 8„=0,1%. 11. 1,5; 0,3%. 12. 39±0,2 (см). 13. 300; одна значащая цифра.

16. 0,3%. 17. 0,94; верные цифры 9 и 4. 18. 2,51 ±0,005. 22. 0,4%. 23. 0,06%.

26. ДА=ДЯ=0,004 см. 27. До 0,01 м. 34. 1) 5=27°,4, о=23,8, *=12,2; 2) А = =41°,1, а=42,3, 6=48,4; 3) 5=61°,5, о=298, 6=549; 4) А=47°,3, а=0,430, 6= =0,397. 35. 1) 5= 37°,7, 6=275, с=450; 2) А = 53°,6, 6=6,32, с= 10,6;

3) А = 17°,4; о=0,297, с=0,993; 4) 5=33°,2; 6=31,4, с=57,3. 36. 1) Л=4Г,3, 5=48°,7, 6=28,3; 2) Л=41°,8, 5=48°,2, о=20,4; 3) Л=53°,3, 5= 36°,7, о=150;

4) А =46°,9, 5=43°,1, 6 =0,428. 37. 1) Л = 51°,6, 5=38°,4, с =1,05; 2) А=1Т, В= 13°, с=431; 3) Л = 31°,6, 5=58°,4, с=2,79; 4) А=37,°2, 5=52°,8, с=41.

38. 1) А=95°,6, а=83,4; 2) В= 77°,7, а=30,7; 3) А=23°,6, 6= 308; 4) 5=21°,8, 6=3,04; 5) Л = 103°,6, а=1080, 6= 686; 6) 5=57°,7, а=53,8, 6=50,4;

7) А = 50°,8, 5=64°,6; 8) Л = 130°,6, 5=24°,7, о=210; 9) Л=21°,8, 5=79°,1, 6=8,41; 10) А = 20°,8, 5=79°,6, а=12,8; 11) 5=61°,9, а=59,9, 6=63,5; 12) Л = 80°,8, 5=49°,6, 6=33,1. 44. 1) с=71,4, Л = 67°,4, 5=47°,8; 2) о=669, 5=47°,2, с=84°,5; 3) 6=6,96, Л =46°,6, с=69°,7; 4) с=689, Л = 30°, 5=37°,8. 45. 1) 5= 39°,3, а=981, с=959; 2) Л = 22°,2, а=23,9, 6=57,2; 3) 5=76°,6, 6=7,99, с=7,4; 4) С=76°,3, а=111, 6= 236. 46. 1) А = 59°,7, 5=55°,7, С=64°,6;

2) Л = 126°,3, 5=20°,5, С= 33°,2; 3) /1=130°,5, 5=32°,6, С=16°,9; 4) Л=44°,4, 5=53°,2, С=82°,4. 47. 1) 5= 59°,7, С=52°,1, с=218; 2) I случай: 5=83°,4; С=33°,9, с=22,9; II случай: 5=96°,6, С=20°,7, с=14,5; 3) 5=33°,5, С=104°, с= 12,6°; 4) I случай: Л = 82°,2, С=49°,6, о=829; II случай: А = 1°,5, С=130°,3, 0=21,2. 48. 3,7%. 49. 0,035. 50. 1,2%. 51. 1%. 52. 364 000 см³; верными являются цифры 3 и 6. 53. 7,9 ±0,03 (см); верными являются цифры 7 и 9. 54. До 0,2 см. Зачетная работа. I вариант.

а=4,38; £„=0,02%; 2) 3600; верные цифры 3 и 6; 3) 63,4±0,1; 4) 0,1%; 5) до 0,02 м. II вариант. 1) о=0,67; £„=0,15%; 2) 3800; верные цифры 3 и 8;

3) 2,85± 0,004; 4) 0,02%; 5) до 0,05.

Глава 3

4. 1), 2) Да; 3) нет. 5. 1) 0; 2) 2/3; 3) 1/4; 4) нет решения. 6. 1) 10/19;

1) —3; 3) 3; 4) —21. 7. 1) 2; 2) 2; 3) 2,5; 4) —1; 5) нет решения; 6) х—любое действительное число, кроме х= ±4. 8. 35 л. 9. Меди 86,1 кг, цинка 36,9 кг.

10. 240 кг. 11. 637,5 и 212,5. 12. 85. 13. 6 см. 15. 1) -\<х< + оо; 2) -2<х< <+оо; 3) — оо<х<3; 4) 2<x<-foo. 16. 1) 0,96<х< + оо; 2) 56<х<4оо;

2) — оо<х< — 35; 4) — оо <х^2,2. 17. 1) — 2<х< 4 оо; 2) —со<х< —3; 3) 1^ <х<4оо; 4) 0,5 < jc < 4 оо. 18. 1) — оо<х< 4-оо; 2) — оо<х<4оо; 3) —оо< <х< + оо. 19. 1), 2) Нет решения. 23. 1) 1<х<4; 2) — оо<х<—3; 3) нет решения; 4) — 2<х< + оо. 24. 1) 1,5<х<4оо; 2) — оо<х< — 3,5; 3) нет решения; 4) 0,25<jc<0,5. 25. 1) — оо<х<1 или 3<х<4оо; 2) — оо<х<10;

— оо <х< + оо; 4) —7<х<4оо. 26. 1) — оо<х< — 2 или 5<х<+оо;

2) — 8<х< + оо; 3) — оо<х<1,2 или 7<х<4оо; 4) — оо<х<4оо. 27.

1) — оо<я< — 3/2 или — 1/3<ж + оо; 2) — со<т<2/3 или 5^т< + оо;

3) — оо<х<1/3 или 4<х<4оо; 4) 2^у<4. 28. 1) —2/3<х< —1/2; 2) 1/2< ^у<4/3; 3) —оо<а<4 или 5<а< + оо; 4) — оо<х<3 или 4<х<4оо.

29. 1) — оо <х< —2/3 или — 1/4<х<+оо; 2) 2,5<х< 11; 3) — оо<а^ — 2 или

0,5<я< 4оо; 4) 2,5<т< 12; 5) —2<а< — 1,5. 33. 1) 4; 2) 1; 3) 1; 4) 2/3.

34. 1) — 2<х<6; 2) — 9<х<—7; 3) — 12<х<—2; 4) я—£<х<я+е; 5) 2^ <х<4. 35. 1) — оо <х< —5 или — 1 <х< 4- оо; 2) — оо <х< —3 или 13<х<4оо; 3) — оо<х< 1 или 3<х<4оо; 4) — оо<х<—3 или — 1<х<

+ оо; 5) — оо <х<0,5 или 1,5^х< +оо. 38. 1) (3; 4); 2) нет решения; 3) бес­конечное множество решений; 4) (2; 3); 5) (—3; —5); 6) (—2; 4). 39. 1) (—2; 2);

2) (3; 0,5); 3) (5; -2); 4) (0; -6,2). 40. а=3. 41. в=1,5. 42. 74. 43. 16 и 12 м

44. 12 и 15 руб. 45. 150 и 80 км. 46. 60 и 70°. 47. 200 и 150. 50. 1) 87; 2) -6

3) 0; 4) 42. 51. 1) (8; 4; 2); 2) (9; 6; 7); 3) (3; -2; 5); 4) (1; -2; 3); 5) (1; 2; 3)

6) (1; 1; 1); 7) (3; 5; 6); 8) бесконечное множество решений. 54. 1) х₁=—_у/2 Хг — у/2; 2) xi = 0; х₂ = 1; 3) Х!=0; х₂ = 3; 4) Xi= — 5; х₂ = 5; 5) нет решения

*!=0; х₂ = 0,4; 7) xi = — 5; х₂=0; 8) х_х = — 5; х₂ = 0. 55. 1) x_t = 2; х₂=4

2) х_х = — 5; х₂= —4; 3) xi = —4; х₂ = 3; 4) х_х = 2/3; х₂ = 2; 5) х₁ = — 0,75; х₂ = = —0,25; 6) Xi = —0,8; х₂ = 6; 7) х=2; 8) нет решения. 56. 1) x_t = — 3; х₂ = 8

2) Х! = 15,8; х₂=18; 3) х₁ = —0,7; х₂=10; 4) xi = —0,5; х₂=2. 61. 1) xi = l; х₂ = = 3; 2) xi=2; х₂ = 5; 3) Xi = — 3; х₂ = 5; 4) Xi = — 3; х₂ =4; 5) xi = —4; х₂=— 2

6) Xi = — 5; х₂ = 3. 62. 1) *²—13х+40 = 0; 2) х² + Зх-10=0; 3) х² + 9х+20=0;

4) 15х² —22x4-8=0; 5) 32х²-4х-3 = 0; 6) 30х² + 37х+10 = 0; 7) 4х²-17х+ +4=0; 8) Зх² —8х—3=0. 63. 1) Корни имеют разные знаки; больший по модулю корень отрицателен; 2) знаки корней различны; больший по модулю корень положителен; 3), 4), 6) оба корня положительны; 5) оба корня отрицательны. 64. 1) (2х—1)(х—3); 2) (2а43) (За—2); 3) (3^44) (у—5);

4) (Зх+1)(4л:+1); 5) (/и+1)(т-3); 6) (8х-3) (9х-5). 65. 1) 2) ^У+Ъ ■

х+З’ ’ 2у+5'

2) Xi = —2; *2 = 1; *з = 3; x₄ = 4; 3) Xt = — 4; x₂= — 2; x₃ = 1; x₄ = 3; 4) х_г = = — 1/2; x₂=l; x₃ = 3; 5) Xx = —3; x₂= — 1; x₃ —0; x₄=4; 6) Xi = —2; x₂ = l; x₃ = 3. 74. 1) x³ + 2x² — 5x—6=0; 2) 6x³—x²—4x—1 =0. 75. 1) Xi=— 3; x₂ = 3;

2) x= —0,4; 3) Xi = —2,5; x₂ = 2,5; 4) x=0,6. 76. 23 и 24. 77. 3/5. 78. 24.