
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление статических моментов плоской фигурыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
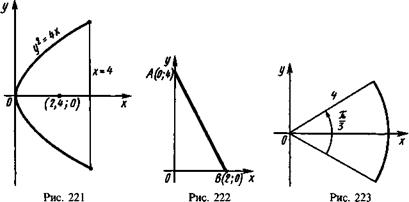
Статическим моментом материальной точки относительно некоторой оси называется произведение массы точки на расстояние до оси. Статические моменты Sx и Sy плоской фигуры D с переменной плотностью 5 (х, у) относительно координатных осей Ох и Оу вычисляются по формулам Sx=JJ yb (х, у) dx dy, Sy=JJ x 8 (x, y) dx dy. (29.20) D D Если фигура D является однородной (плотность 5 постоянна), то Sx=btfydxdy, Sy = b\\xdxdy. (29.21) D D 58. Найти статические моменты относительно координатных осей фигуры, ограниченной параболой у2=х (у^О) и прямой х=4, если плотность 8 распределения массы в каждой точке равна абсциссе этой точки. О Согласно условию, 8=х. Область D определяется системой неравенств 0<х<4, О^у^у/х. Используя формулы (29.20), получим Sx=^dx J ydy=-j[y2lQXdx=- xdx =4 (куб. ед).; D ООО О Vx 4 4 Sy = Qx2 dxdy=^x2 dx J dy=^\y^x x2 dx—^x5'2 dx—Ъб- (куб. ед). ф D ООО о 59. Найти статический момент пластинки в форме полукруга х2+y2 = R2 относительно диаметра, если ее плотность 5=1. О Согласно формуле (29.20), статический момент относительно оси Ох есть Sx—tfydxdy. Перейдем к полярным координатам; тогда R=r и у = ____ D_ = y/R2 — x2 -=у/R2 — г2 cos2 ф =rsin ф. В силу симметрии области D относительно оси Оу возьмем 1/2 этой области, которая определяется системой неравенств 0<ф<тс/2, Следовательно, Я/2 R я/2 Sx=2 j*Jrsin ф-rdrdq> = 2 j* sinфdq> Jr2<ir=^ J [r3]* sin ф</ф = D 0 0 0 Я/2 2R3 f., 2R 3 Г 1,2 2R3, r =— sin ф dip = - — [cos ф^/2 =— (куб. ед.). * о 60. Найдите статические моменты относительно осей Ох и Оу однородных пластинок (5=1), имеющих формы: 1) прямоугольника 0<лс^4, 0<^<6; 2) треугольника с вершинами О (0; 0), А (6; 0), В (0; 8); 3) полукруга x2+j;2 = 16, у^0; х2 у2 4) эллипса — + —= 1, ограниченного положительными полуосями Ох и Оу; 5) параболы у=х2, х^0, у=4. 61. Пластинка имеет форму прямоугольного треугольника с катетами ОА = 3, ОВ—4, причем ее плотность в любой точке пластинки равна расстоянию этой точки от катета О А. Вычислите статические моменты пластинки относительно катетов О А и ОВ. 62. Найдите статические моменты относительно осей Ох и Оу пластинки, ограниченной прямыми х—3у = 0, 2х+3у—18 = 0 и осью Оу, если плотность в любой точке пластинки равна ординате этой точки. КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Координаты центра тяжести (.хс; у с) плоской фигуры с непрерывной массой и переменной плотностью 5 = 5 (х, >>) вычисляются по формулам
Или в другой форме записи
где m—масса фигуры, Sy, Sx—статические моменты относительно осей координат.
xc=-JJ хахау, yc^-^ydxay. (29.24) D D В полярной системе координат формулы (29.24) имеют вид хс=]; JJr2 cos Ф drdq>, JJr2 sin ф^г^ф. (29.25) D D
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.007 с.) |


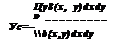
 (29.23)
(29.23) Если фигура D является однородной (5 = const) и S—площадь этой фигуры, то координаты центра тяжести находятся по формулам
Если фигура D является однородной (5 = const) и S—площадь этой фигуры, то координаты центра тяжести находятся по формулам


