
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площади плоской фигурыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Площадь S плоской области D в прямоугольных координатах вычисляется по формуле
D А в полярных координатах—по формуле S=\\rdrdq>. D
32. Вычислить площадь области, ограниченной линиями у=х2 и у=х+6. О Найдем точки пересечения данных линий (рис. 213): \у =х2, 9 Область D запишем в виде системы неравенств \у=х+6, М(3; 9), N(-2; 4). Р —2ис^3, х2^у^х+6. Согласно формуле (29.13), получим х+6 3 3 5= j* dx J dy= J* \yYj6<lx= J (x+6-x2)dx=
33. Вычислить площадь области Д заданной неравенствами я/4<ср<я/3, 2<г<4 (рис. 214). О Используя формулу (29.14), находим Я/3 4 tfrdrd(f>= |*</<р|г</г= Я/4 2 Я/3 я/3 | [г2]5<*Р=6 |<*Р=6[<р]^4=^(кв. ед.; Я/4 я/4 34. Вычислить в полярных координатах площадь области D, ограниченной окружностью х2-\-у2—4х=0 и прямыми ^ = 0, у=х. О Найдем точки пересечения окружности и прямой: (х2+у (/=■*> Для построения окружности преобразуем ее уравнение: х2 —4x4- 4- 4+у2=4, (х—2)2+у2=4, откуда следует, что центр окружности есть точка Ох (2; 0), a Я = 2. Для вычисления искомой площади в полярных координатах находим г и ф. Учитывая, что х=г совф и у=г втф, запишем данное уравнение х2 4- у2—4х=0 в полярных координатах: г2cos2ф4-г2sin2ф—4rcosф=0. Упростив его, получим г2 (cos2<p + sin2(p)—4rcos(p=0, г2—4гсовф = 0, rt=0, г2 = =4со8ф. Теперь находим угол ф: tg ф =_у/л:= 2/2 = 1, ф = я/4. Следовательно, область D определяется системой неравенств 0<ф<я/4, 0<г<4со8ф. Согласно формуле (29.14), находим
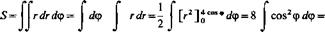 
35. Вычислите площадь плоской фигуры в прямоугольных координатах, если область D ограничена линиями: 1) у=%/х, у=-х+ 9; 2)у=4/х, у=х, у= 4; jv=sin л:, j=cosjc, х=0; 4).y=cosx, х=0, 1; 5) у2 = 4х, у=х; 6) у=х2, у = —х2 + 2, л: = 0. 36. Вычислите в полярных координатах площади областей, ограниченных заданными линиями: 1) г=4, ф = л/6, ф = 7с/3; 2) r= 1, г=2, ф = я/6, ф = 7t/4. 37. Вычислите площадь области Д заданной в полярных координатах системой неравенств 0<ф<я/2, О^г^Зсовф. 38. Вычислите площадь фигуры, ограниченной окружностями r= 1 и г=2совф (вне окружности r= 1). § 6. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА Объем цилиндрического тела, ограниченного сверху поверхностью z=f(x9 у), снизу плоскостью z—0 и сбоку прямой цилиндрической поверх- ностью, вырезающей на плоскости xOy(z=0) область D (рис. 216), вычисляется по формуле
39. Выделить объем тела, ограниченного поверхностями z=2x+l, х=0, у=4, у=х2. О Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в I октанте. Сверху тело ограничено плоскостью z=2x+l, сбоку параболическим цилиндром у=х2 и плоскостями х=0 и у=4, снизу параболой у=х2 и прямыми рс=0 и у=4. Найдем точки пересечения параболы у=х2 и прямой у=4: ^ , Значение х=—2 не рассматриваем, так как цилиндр {/=4, М(2; 4). расположен в I октанте. Область D запишем в виде системы неравенств 0<х<2, х2^у^4. Согласно формуле (29.15), получим 4 2 V= Jdx j*(2x+ l)dy=j[2xy+y]42dx= d о x2 0 =j*(8x+4—2x3—x2)dx=13^(Ky6. ед.) • о 40. Вычислить объем тела, ограниченного поверхностями z = 3—x—y, х2+у2= 1 и z=0. О Данное тело есть прямой круговой цилиндр, ограниченный сверху плоскостью z—3—х—у, а снизу—кругом jc2 = 1 в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств -l^x^l, -у/\-х2^у^у/\-х2.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.209.178 (0.006 с.) |

 S=\$dxdy,
S=\$dxdy,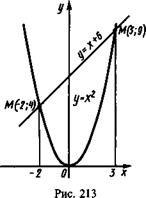 =[у+6х“т].2=20^(кв ед)- •
=[у+6х“т].2=20^(кв ед)- •
 о
о
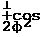
 V=\\zdxdy. (29.15)
V=\\zdxdy. (29.15)


