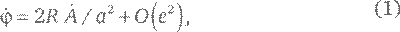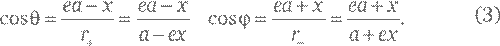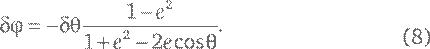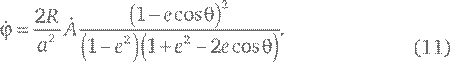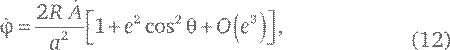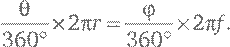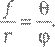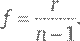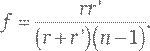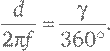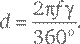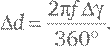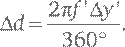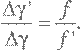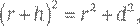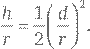Правило равных площадей и эквант

 

Согласно Первому закону Кеплера, все планеты, включая Землю, обращаются вокруг Солнца по эллиптическим орбитам, причем Солнце находится не в их центрах, а в некоторых смещенных от центра точках, расположенных на больших осях этих эллипсов – в одном из фокусов эллипса каждой из орбит (см. техническое замечание 18). Эксцентриситет эллипса e определяется так, что расстояние от любого его фокуса до центра равно ea, где a – длина большой полуоси эллипса. Также, согласно Второму закону Кеплера, скорость каждой планеты при ее перемещении по орбите не постоянна, а изменяется таким образом, что отрезок (или радиус-вектор), проведенный к ней от Солнца, заметает равные по площади участки плоскости за одинаковые отрезки времени.

Существует другой способ приближенно сформулировать тот же Второй закон, имеющий близкое отношение к старой идее экванта, которую использовал в своей астрономической системе Птолемей. Вместо того чтобы рассматривать отрезок, проведенный к планете от Солнца, рассмотрим отрезок к ней же из другой точки, а именно из пустого фокуса ее эллиптической орбиты. Эксцентриситет e некоторых орбит планет довольно значителен, и им нельзя пренебрегать. Но его квадрат e ² очень мал для любой планеты. Например, среди планет самый большой эксцентриситет у орбиты Меркурия, для него e = 0,206, а e ² = 0,042; для Земли же e ² = 0,00028. Поэтому при вычислении планетных движений достаточно аппроксимировать реальные их законы уравнениями, в которых присутствуют слагаемые, пропорциональные эксцентриситету e, или независимые от него слагаемые, и игнорировать такие их члены, которые пропорциональны квадрату эксцентриситета e ² или его степеням высших порядков. В этом приближении Второй закон Кеплера эквивалентен утверждению, что отрезок, проводимый из пустого фокуса планетной орбиты к планете, заметает равные углы за равные промежутки времени. Иначе говоря, эта линия вращается с постоянной угловой скоростью.

На конкретном примере покажем, что если

– это скорость, с которой радиус-вектор от Солнца к планете заметает равные площади, а

(фи с точкой) – скорость изменения угла между радиус-вектором от пустого фокуса к той же планете и большой осью ее орбиты, то верно равенство

 

 

где O (e ²) – обозначение всех членов, пропорциональных e ² или степеням e еще более высоких порядков, а R – коэффициент, значение которого зависит от применяемых единиц измерения углов. Если мы меряем углы в градусах, то R = 360°/2 π = 57,293…°, то есть угол размером в один радиан. Или мы можем измерять углы в радианах, и тогда R = 1. Второй закон Кеплера гласит, что за одинаковые промежутки времени площадь, заметаемая радиус-вектором планеты, одна и та же. Это значит, что

– величина постоянная, а, следовательно, что постоянна и с точностью до слагаемых высшего порядка, пропорциональных e ². Поэтому с достаточной точностью можно сказать, что за заданный промежуток времени угол, на который изменяется радиус-вектор планеты из пустого фокуса ее орбиты, всегда один и тот же.

Что касается описанной Птолемеем теории, центр эпицикла каждой планеты обращается вокруг Земли по круговой орбите, деференту, но Земля находится не в центре деферента. Орбита является эксцентричной, то есть Земля находится в точке, отделенной от центра деферента небольшим расстоянием. Мало того, скорость, с которой центр эпицикла обращается вокруг Земли, не постоянна, и угловая скорость, с которой луч от Земли к этому центру поворачивается, тоже не постоянна. Чтобы детально учесть все особенности наблюдаемого движения планет, Птолемей изобрел понятие экванта. Это точка по другую сторону от центра деферента по отношению к Земле, которая находится на том же расстоянии от центра, что и Земля. Луч, проводимый к центру эпицикла от этого экванта (а не от Земли), и должен был описывать равные углы в одни и те же промежутки времени.

Внимательный читатель уже заметил, что это очень похоже на картину, описываемую законами Кеплера. Конечно, роли Солнца и Земли в астрономических системах мира Птолемея и Коперника противоположны, но пустой фокус эллипса в теории Кеплера играет ту же самую роль, что и эквант в теории Птолемея, а Второй закон Кеплера объясняет, почему введение экванта помогло улучшить теоретические предсказания видимых положений планет по теории Птолемея.

 

Теперь докажем равенство (1). Определим θ как угол между большой осью эллипса и отрезком, соединяющим Солнце и планету, и вспомним, что φ определен как угол между той же большой осью и отрезком, соединяющим планету и пустой фокус. Так же, как в техническом замечании 18, обозначим длины этих отрезков r + и r – то есть расстояния от Солнца до планеты и от планеты до пустого фокуса орбиты соответственно. Как было показано, они равны

 

 

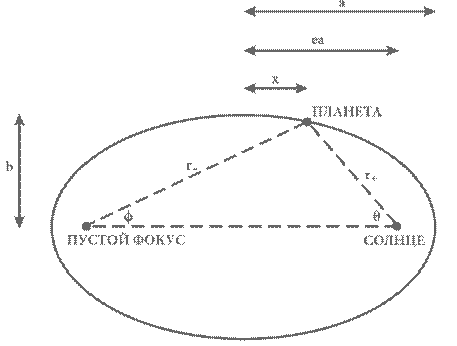
где х – горизонтальная координата точки на эллипсе, то есть расстояние между точкой и прямой, секущей эллипс вдоль его малой оси.

Косинус угла определяется в тригонометрии с использованием прямоугольного треугольника, один из углов которого равен данному: косинусом называется отношение длины катета, прилежащего к этому углу, к длине гипотенузы треугольника. Поэтому из рис. 15 мы можем записать:

 

 

 

Рис. 15. Орбитальное движение планеты по эллипсу. Орбита планеты вычерчена здесь как эллипс, имеющий эксцентриситет (как и на рис. 12) около 0,8 – значительно больше, чем у какой-либо планеты Солнечной системы. Отрезки, обозначенные r + и r−, соединяют планету, соответственно, с Солнцем и с противоположным ему, пустым фокусом эллипса.

Уравнение слева мы можем решить, найдя из него x:

 

 

Подставляя результат в формулу для cos φ, выражаем связь между углами θ и φ:

 

 

Поскольку равенство справедливо при любых значениях угла θ, изменение в левой части равенства должно быть равно изменению в правой части при любом изменении θ. Допустим, мы производим бесконечно малое его изменение δθ (дельта тета). Чтобы рассчитать, насколько изменится φ, прибегнем к правилу дифференциального исчисления, согласно которому изменение любого угла α (это может быть θ или φ) на величину δα (дельта альфа) приводит к изменению cos α на величину – (δα/ R) sin α. Оттуда же при изменении любой функции f, такой, например, как знаменатель в уравнении (5), на ничтожно малую величину δ f изменение в отношении 1/ f составляет −δ f / f 2. Приравняв соответствующие изменения с обеих сторон равенства, получаем:

 

 

Теперь нам нужна формула, связывающая sin φ и sin θ. Для этого посмотрим на рис. 15 и обратим внимание, что вертикальная координата y точки на линии эллипса выражается как y = r + sin θ, а также y = r − sin φ, и, поделив их, сократив y, получаем:

 

 

Совмещая уравнения (7) и (6), имеем:

 

 

Итак, какова же площадь, описываемая радиус-вектором планеты, проведенным от Солнца, когда угол θ изменяется на δθ? Измеряя углы в градусах, мы можем сказать, что это площадь равнобедренного треугольника, две равные стороны которого имеют длину r +, а третья – маленькая часть дуги общей длиной 2 πr + окружности радиусом r +, равная 2 πr + × δθ/360°. Она равна

 

 

В этой формуле поставлен минус, поскольку мы хотим, чтобы величина δ A росла, если увеличивается угол φ; но если вспомнить, как мы определили эти углы, φ будет расти в том случае, если уменьшается θ, поэтому δφ больше нуля, когда δθ меньше нуля. Поэтому уравнение (8) можно переписать в виде:

 

 

Принимая, что δ A и δφ – описываемая первым радиус-вектором площадь и угол поворота второго радиус-вектора за ничтожно малый промежуток времени δ t, и поделив обе части уравнения (10) на δ t, найдем соответствие между описываемыми площадями и углами в виде равенства

 

 

Нами получено точное равенство. Но теперь посмотрим, как оно себя ведет в том случае, когда e очень мал. Числитель второй дроби в уравнении (11) имеет вид (1 − e cos θ)² = 1 − 2 e cos θ + e ²cos²θ, так что слагаемые нулевого и первого порядка в числителе и знаменателе дроби одни и те же, и вся разница между числителем и знаменателем заключается в коэффициентах членов, пропорциональных e ². И значит, уравнение (11) полностью соответствует искомому нами с самого начала равенству (1). Для большей определенности мы можем оставить в уравнении (11) члены порядка e ²:

 

 

где O (e ³) обозначает члены, пропорциональные e ³ или более высоким степеням e.

 

Фокусное расстояние линзы

 

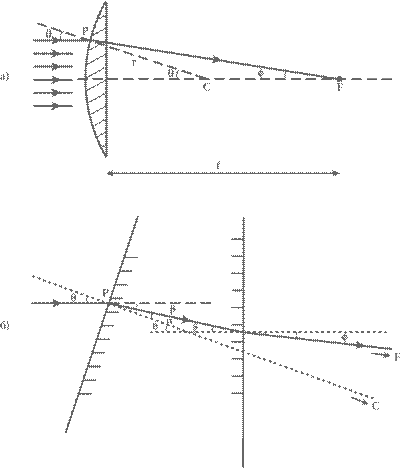
Рассмотрим поставленную вертикально линзу с выпуклой передней стороной и плоской задней – похожие линзы Галилей и Кеплер использовали для изготовления объективов своих телескопов. Из криволинейных поверхностей легче всего полировать сферические, и мы допустим, что форма передней поверхности линзы – сегмент сферы радиусом r. Также в наших рассуждениях будем считать, что линза тонкая, то есть ее максимальная толщина значительно меньше, чем r.

Пусть луч света горизонтально падает на линзу параллельно ее оси и встречается с поверхностью линзы в точке P. В этом случае отрезок от расположенного позади линзы центра кривизны C сферической поверхности до точки P образует с центральной осью линзы угол θ. Линза преломит луч света таким образом, что после того, как он выйдет из ее толщи через заднюю поверхность, он пересечет ось под другим углом, который мы обозначим φ. Точку его пересечения с осью симметрии линзы обозначим F (см. рис. 16а). Нам требуется рассчитать расстояние f, которое отделяет эту точку от линзы, и доказать, что оно не зависит от θ, за счет чего все параллельные лучи, падающие на линзу горизонтально, пересекают ее центральную ось в точке F. Говорят, что в этом случае лучи фокусируются линзой в точке F, а расстояние f от нее до линзы называется фокусным расстоянием.

Для начала обратим внимание, что длина дуги вдоль передней поверхности линзы от оси линзы до точки P есть доля θ/360° от полной длины окружности, образующей сферы 2 πr. С другой стороны, та же самая дуга составляет φ/360° от полной длины окружности радиусом f, которая равна 2 πf. Будем считать, что эти две дуги одинаковые, и приравняем их:

 

 

Теперь, сокращая в правой и левой частях 360° и 2 π, получаем пропорцию:

 

 

Значит, чтобы рассчитать фокусное расстояние линзы, нужно найти отношение φ к θ.

Для этого нужно обратить внимание, что именно происходит с лучом света внутри линзы (см. рис. 16б). Отрезок от центра кривизны C до точки P, в которой горизонтальный луч падает на линзу, перпендикулярен выпуклой сферической поверхности линзы в точке P, поэтому угол между этим перпендикуляром и лучом (то есть угол падения луча) равен θ. Как известно еще со времен Клавдия Птолемея, если угол θ достаточно мал (а для тонкой линзы так и есть), то угол α между направлением луча в толще стекла и тем же перпендикуляром (то есть угол преломления луча) пропорционален углу падения:

 

 

α = θ/n,

 

где n > 1 – постоянная величина, называемая коэффициентом преломления, которая зависит от свойств стекла и окружающей среды – чаще всего это воздух (Ферма показал, что n равно скорости света в воздухе, деленной на скорость света в стекле, но нам это знать необязательно). В таком случае угол β между лучом света в толще стекла и осью линзы равняется:

 

 

β = θ − α = (1 − 1/n)θ.

 

Рис. 16. Фокусное расстояние линзы: а) определение фокусного расстояния. Горизонтальная штриховая прямая – оптическая ось линзы. Линии со стрелками обозначают направление лучей света, падающих на линзу параллельно ее оси. Мы рассматриваем один луч, который падает на линзу в точке P, в которой он образует малый угол θ, с перпендикулярной поверхности прямой, проходящей через точку P и центр кривизны C поверхности линзы. Этот луч преломляется линзой, выходя из нее идет под углом φ к оси линзы и пересекает ее в точке F, находящейся на расстоянии f от линзы. Это расстояние и называется фокусным. Поскольку θ пропорционален φ, все горизонтальные лучи собираются линзой в этой точке; б) вычисление фокусного расстояния. Здесь показан маленький фрагмент линзы, где наклонная сплошная линия со штриховкой слева обозначает небольшой сегмент передней выпуклой поверхности линзы. Сплошная линия со стрелкой отмечает путь луча, преломляемого линзой, который входит в ее толщу в точке P под небольшим углом θ к перпендикуляру к поверхности в этой точке. Этот перпендикуляр показан на чертеже как наклонная пунктирная линия – часть прямой, проходящей через точку P и центр C кривизны поверхности линзы, который не показан, потому что находится за границей этого чертежа. Входя внутрь линзы, луч преломляется и образует угол α с этим перпендикуляром, а покидая ее, преломляется снова, образуя угол φ с перпендикуляром к плоской задней поверхности линзы. Этот второй перпендикуляр показан на чертеже как пунктирная прямая, параллельная оптической оси линзы.

 

Это угол между лучом света и перпендикуляром к плоской задней поверхности линзы, под которым луч достигает этой поверхности. Однако, когда луч выходит сквозь заднюю поверхность, он образует другой угол – φ по отношению к перпендикуляру к этой поверхности. Соотношение между углами φ и β такое же, как в случае, если бы свет шел в противоположную сторону: тогда φ был бы углом падения, а β – углом преломления, то есть β = φ/ n, и, следовательно:

 

 

φ = nβ = (n − 1)θ.

 

Отсюда мы видим, что угол φ прямо пропорционален θ, и значит, используя нашу ранее полученную формулу для отношения f / r, получаем:

 

 

Это равенство не зависит от θ, так что, как я и обещал, все лучи света, падающие на линзу горизонтально, собираются ею в одну и ту же точку на ее оси симметрии.

Если радиус кривизны r очень большой, кривизна у передней поверхности линзы маленькая, и поэтому линза ведет себя почти как плоский кусок стекла – преломление света на входе в линзу почти компенсируется преломлением на выходе. Также, если коэффициент преломления n близок к 1, линза очень слабо преломляет свет, какой бы формы она ни была. И в том, и в другом случае фокусное расстояние будет очень большим, и тогда мы говорим, что такая линза слабая. Сильная же линза – это линза со средним радиусом кривизны и коэффициентом преломления, существенно отличающимся от 1. Например, для стеклянной линзы n ≈ 1,5.

Похожий результат получается и в том случае, если задняя поверхность линзы не плоская, а представляет собой сегмент сферы радиусом r’. В этом случае фокусное расстояние рассчитывается как:

 

 

Результат получается таким же, как раньше, в том случае, если r’ значительно больше r, – тогда задняя поверхность получается практически плоской.

Понятие о фокусном расстоянии можно распространять и на вогнутые линзы, как, например, такую линзу, которую Галилео Галилей использовал в качестве окуляра своего телескопа. Вогнутая линза может превратить сходящийся пучок лучей света в параллельный или даже в расходящийся. Можно определить фокусное расстояние линзы, рассматривая такой сходящийся пучок лучей, который она выпрямляет: тогда фокусным расстоянием будет расстояние от линзы до той точки, где исходные лучи сошлись бы, если бы линзы на их пути не было. И хотя у него иной смысл, фокусное расстояние вогнутой линзы рассчитывается по формуле, аналогичной той, которую мы вывели для выпуклой линзы.

 

Телескоп

 

Как мы видели в техническом замечании 22, тонкая выпуклая линза будет фокусировать лучи света, которые падают параллельно ее центральной оси, в точке F на этой оси, на расстоянии за линзой, которое называется фокусным расстоянием f для этой линзы. Параллельные лучи света, которые падают под небольшим углом γ к центральной оси, также будут фокусироваться этой линзой, но в точке, которая немного смещена от центральной оси. Чтобы увидеть, как далеко она сместится, мы можем мысленно повернуть путь луча на рис. 16а вокруг линзы на угол γ. Расстояние d от фокуса до центральной оси линзы составит тогда ту же долю длины окружности радиусом f, что и угол γ от 360°:

 

 

Следовательно,

 

 

Это работает только для тонких линз; иначе d также зависит от угла θ, упомянутого в техническом замечании 22. Если лучи света от какого-либо далекого объекта падают на линзу под углами, попадающими в промежуток Δγ (дельта гамма), то они будут фокусироваться на вертикальном отрезке длиной Δ d, значение которого можно выразить как:

 

 

Как обычно, эта формула становится проще, если измерять Δγ в радианах, равных 360°/2 π, а не в градусах. В таком случае она читается просто как Δ d = f Δγ. Этот участок, где фокусируется свет, называется мнимым изображением (см. рис 17а).

Мы не можем увидеть мнимое изображение, просто посмотрев на него, потому что после того, как оно получается, лучи света снова рассеиваются. Чтобы сфокусироваться в точке на сетчатке расслабленного человеческого глаза, лучи света должны войти в него по более или менее параллельным направлениям. В телескопе Кеплера была вторая выпуклая линза, которую называют окуляром, чтобы фокусировать расходящиеся лучи света от мнимого изображения так, чтобы они параллельно выходили из телескопа. Повторив те же рассуждения для лучей света, идущих в противоположном направлении, мы увидим, что для того, чтобы лучи света, расходящиеся от точки, покидали телескоп по параллельным направлениям, окуляр должен находиться на расстоянии f ′ от мнимого изображения, где f ′ – это фокусное расстояние окуляра (см. рис. 17б). Это означает, что длина телескопа L должна составлять сумму фокусных расстояний:

 

 

L = f + f ′.

 

Промежуток Δγ’ направлений лучей света, входящих в глаз от различных точек источника, связан с размером мнимого изображения по формуле:

 

 

 

Рис. 17. Телескопы: а) формирование мнимого изображения. Две сплошные линии со стрелками обозначают лучи света, которые входят в линзу и разделены небольшим углом Δγ. Эти линии (и другие, параллельные им) фокусируются на расстоянии f от линзы на вертикальном отрезке длиной Δ d, пропорциональной Δγ; б) линзы в телескопе системы Кеплера. Линии со стрелками обозначают путь лучей света, которые идут к слабой выпуклой линзе от далекого объекта по практически параллельным направлениям; фокусируются с помощью линзы в точке на расстоянии f от линзы; расходятся от этой точки и преломляются сильной выпуклой линзой, чтобы войти в глаз наблюдателя по параллельным направлениям.

 

Видимый размер объекта пропорционален углу, под которым видны противоположные стороны удаленного объекта, поэтому увеличение телескопа равно отношению угла, под которым лучи света от краев объекта, выходящие из окуляра, входят в глаз наблюдателя, к углу, под которым они входили бы, если бы телескопа не было:

 

 

Подставив в это соотношение две формулы, которые мы вывели для определения размера Δ d мнимого изображения, мы увидим, что увеличение равно:

 

 

Чтобы получить значительное увеличение, нам нужно, чтобы линза в передней части телескопа была намного слабее окуляра, то есть f >>f ′.

Это не так уж легко сделать. В соответствии с формулой фокусного расстояния, данной в техническом замечании 22, чтобы получить сильный стеклянный окуляр с коротким фокусным расстоянием f ′, его линза должна иметь маленький радиус кривизны, что означает, что она либо должна быть очень маленькой, либо не должна быть тонкой (то есть толщина должна быть намного меньше радиуса кривизны). В обоих этих случаях окуляр не сможет хорошо фокусировать свет. Вместо этого мы можем взять слабую переднюю линзу с большим фокусным расстоянием f, но в таком случае длина телескопа L = f + f ′ ≈ f должна быть очень большой. Галилею потребовалось некоторое время, чтобы внести в свой телескоп изменения, давшие ему достаточное увеличение для астрономических целей.

Галилео сделал свой телескоп немного другим – с вогнутым окуляром. Как уже упоминалось в техническом замечании 22, если разместить вогнутую линзу так, чтобы она сводила в одну точку входящие в нее лучи света, они будут выходить по параллельным направлениям. Фокусное расстояние – это расстояние позади линзы, на котором лучи света сходились бы в одной точке, если бы линзы не было. В телескопе Галилея была слабая выпуклая линза впереди с фокусным расстоянием f и сильная вогнутая линза с фокусным расстоянием f ′ позади нее, перед тем местом, где должно было находиться мнимое изображение, если бы вогнутой линзы не было. Увеличение этого телескопа, опять же, составляет f/f ′, но его длина равна только f − f ′ вместо f + f ′.

 

Лунные горы

 

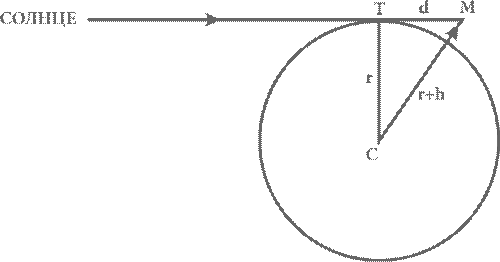
Темная и светлая стороны Луны разделяются границей дня и ночи, называемой терминатором – в этой области солнечные лучи падают по касательной к лунной поверхности. Когда Галилей начал наблюдать Луну в телескоп, он обратил внимание на яркие точки на темной стороне Луны вблизи терминатора и истолковал их как свет, отраженный вершинами гор достаточно высоких, чтобы на них попадал свет солнца, еще не вышедшего из-за горизонта для наблюдателя у подножия горы. Он смог рассчитать высоту этих гор с помощью геометрического построения, похожего на то, которое использовал аль-Бируни, чтобы измерить размер Земли. Начертим треугольник, вершинами которого будут центр Луны C, вершина горы на ночной стороне Луны M, которой едва лишь коснулся первый луч солнца, а также точка на поверхности T, где тот же самый луч скользит вдоль лунной равнины до того, как осветит гору (см. рис. 18). Это прямоугольный треугольник: отрезок TM – часть прямой, касательной к поверхности Луны в точке T, поэтому он должен быть перпендикулярен отрезку CT. Длина CT равна радиусу Луны r, а TM – расстояние между горой и линией терминатора. При условии, что гора имеет высоту h, длина отрезка CM (гипотенузы треугольника) равна r + h. По теореме Пифагора получаем:

 

 

и значит,

 

 

Поскольку высота любой горы на Луне значительно меньше размера самой Луны, то членом h ² можно пренебречь и учитывать только 2 rh. Разделив обе части уравнения на 2 r ², получаем:

 

 

Так, измеряя отношение видимого расстояния вершины горы от терминатора к видимому радиусу Луны, Галилей смог найти отношение высоты горы к радиусу Луны.

 

Рис. 18. Способ, примененный Галилеем, чтобы определить высоту лунных гор. Сплошная горизонтальная линия со стрелкой отмечает луч солнца, который касается поверхности Луны в точке T, где проходит граница дня и ночи, а затем попадает на вершину горы M; высота горы равна h, и она находится на расстоянии d от терминатора.

 

Галилей в «Звездном вестнике» писал, что иногда он наблюдал яркие точки на ночной стороне Луны на видимом расстоянии от терминатора, большем, чем 1/20 видимого диаметра Луны: для таких гор d / r > 1/10, и значит, по выведенной выше формуле h / r > (1/10)²/2=1/200. Галилей оценивал радиус Луны в 1000 миль[322], так что эти горы должны быть как минимум 5 миль (около 8 км) высотой. По неясным причинам Галилей написал «4 мили», но поскольку он лишь стремился дать оценку минимально возможной высоты горы, то мог просто поосторожничать. Галилео считал, что это больше, чем самые высокие горы на Земле, но теперь нам известно, что на Земле есть горы почти 9 км высотой, так что наблюдения Галилея показывают, что горы на Луне по высоте не очень отличаются от земных.