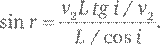Вывод закона преломления света на основе волнового принципа

 

Закон преломления света можно вывести, исходя из предположения о том, что свет движется по пути наименьшего времени, как было описано в техническом замечании 28. Но его также можно вывести и на основе волновой теории света. По мнению Гюйгенса, свет – это колебания какой-то среды, которая может либо быть заполнена прозрачной материей, либо представляться нам пустотой. Фронт возмущения этой среды являет собой прямую линию, которая движется вперед в направлении своего перпендикуляра со скоростью, характерной для среды, в которой он распространяется.

 

Рис. 23. Преломление световой волны. И снова горизонтальная линия обозначает границу раздела двух прозрачных сред, в которых свет движется с разными скоростями. Отрезки с поперечными штрихами обозначают фронт волны в разные момены времени – когда передний край фронта волны входит в контакт с границей и когда задний край теряет контакт с границей. Прямые линии со стрелками указывают траектории перемещения переднего и заднего края волнового фронта.

 

Рассмотрим сегмент такого фронта возмущения длиной L в среде 1, который движется по направлению к границе со средой 2. Допустим, что направление его движения, совпадающее с перпендикуляром к фронту волны, образует с нормалью (перпендикуляром) к этой границе угол i. Когда передний край фронта касается границы раздела сред в точке A, задний его край B еще находится на некотором расстоянии (измеряемом вдоль направления движения волны) от границы, равном L tg i (см. рис. 23). Это значит, что теперь задняя граница фронта волны достигнет пограничной точки D через промежуток времени, равный L tg i / v 1, где v 1 – скорость распространения возмущения в среде 1. В течение того же времени передний край фронта возмущения будет перемещаться в среде 2 под углом r от перпендикуляра к границе раздела сред к точке C, которая расположена на расстоянии v 2 L tg i / v 1, где v 2 – скорость распространения возмущения в среде 2. Когда он пройдет этот путь, волновой фронт, расположенный под прямым углом к направлению своего движения в среде 2, протянется между точками C и D, образуя таким образом прямоугольный треугольник с вершинами A, С и D, в котором угол при вершине C прямой.

Катет AC длиной v 2 L tg i / v 1 – противолежащий углу r в этом треугольнике. Его гипотенуза – отрезок AD, имеющий длину L /cos i (см. рис. 23). Отсюда:

 

 

Вспомнив, что tg i = sin i /cos i, замечаем, что множители cos i и L сокращаются, оставляя:

 

 

Или, если выразить это иначе,

 

 

что и является формулой закона преломления света.

То, что волновая теория света, как доказал Гюйгенс, описывает явление преломления так же, как и принцип наименьшего времени следования, описанный Ферма, вовсе не случайно. Можно показать, что даже в том случае, когда волна движется сквозь неоднородную среду, в которой скорость светового луча плавно меняется в различных направлениях, а не резко на границе раздела сред, из волновой теории Гюйгенса следует, что луч между двумя точками всегда будет следовать по пути наименьшего времени.

 

Измерение скорости света

 

Предположим, что мы наблюдаем какой-либо процесс, происходящий с определенной периодичностью на некотором расстоянии от нас. Для определенности возьмем естественный спутник, обращающийся вокруг далекой планеты, хотя приведенный ниже анализ можно применить и к любому другому периодически повторяющемуся процессу. Предположим, что спутник достигает определенного положения на своей орбите в два следующих друг за другом момента времени t 1 и t 2. Например, это могут быть моменты времени, когда он появляется из-за планеты. Если орбитальный период этого спутника равен T, то t 2 − t 1 = T. Это период, который мы наблюдаем при условии, что расстояние между нами и планетой постоянно. Но если это расстояние меняется, то он будет сдвигаться от Т в ту или иную сторону на значение, которое зависит от скорости света.

Предположим, что расстояние между нами и планетой в два следующих один за другим момента времени, когда спутник находится в одинаковом положении на своей орбите, равно d 1 и d 2. Следовательно, мы наблюдаем эти положения на орбите в моменты времени:

 

 

где с – скорость света (здесь мы предполагаем, что расстоянием между спутником и планетой можно пренебречь). Если расстояние между нами и этой планетой изменяется со скоростью v, независимо от того, двигается ли только она или мы вместе с ней, тогда d 2 − d 1 = vT. Таким образом, наблюдаемый период равен:

 

 

Следствие этой формулы зависит от допущения, что v за временной промежуток T меняется очень мало, что в общем случае верно для Солнечной системы, но v может меняться более ощутимо за временные промежутки, характерные для более масштабных явлений. Когда находящаяся на большом расстоянии планета движется к нам или от нас, скорость v будет отрицательной или положительной и видимый период обращения ее спутника тоже будет соответственно уменьшаться или увеличиваться. Мы можем измерить T, наблюдая планету в момент времени, когда v = 0, а затем измерить скорость света, наблюдая за периодом времени, когда v имеет известное не нулевое значение.

Это основа определения скорости света, которую Гюйгенс вывел, опираясь на наблюдения Рёмера, исследующего изменения видимого орбитального периода спутника Юпитера Ио. Но если скорость света известна, то те же самые расчеты могут дать нам относительную скорость v отдаленного объекта. В частности, световые волны определенных линий спектра далекой галактики колеблются с характерным периодом T, связанным с их частотой ν и длинной волны λ в следующем соотношении T = 1/ v = λ/ c. Эти периоды известны из наблюдений спектров в лабораториях на Земле. Поскольку в начале XX в. было обнаружено, что спектральные линии очень далеких галактик указывают на большие длины волн и, следовательно, на более длинные периоды колебаний, можно сделать вывод, что эти галактики отдаляются от нас.